- Учителю
- Методическая разработка Решение комбинированных уравнений
Методическая разработка Решение комбинированных уравнений
Методическая разработка "Решение комбинированных уравнений"
Предисловие
На вступительных экзаменах, в вариантах ЕГЭ, все чаще предлагаются уравнения с разными функциями: степенными, показательными, логарифмическими, тригонометрическими, так называемые комбинированные уравнения.
Учащиеся, владеющие только стандартными методами решения уравнений, как правило, попадают в расставляемые экзаменаторами ловушки. "Берясь" за решение уравнения, они концентрируют свое внимание только на поиске преобразований, сводящих исходное уравнение к более простому, забывая при этом, что упрощение полезно и возможно не всегда.
Далее речь пойдет о наиболее общих методах, используемых при решении комбинированных уравнений.
1. Метод разложения на множители. Метод введения новой переменной.
Сначала рассмотрим несколько несложных уравнений, иллюстрирующих наиболее распространенную схему решения.
Пример 1.1 Решить уравнение:
![]()
Решение:
ОДЗ: x I (-0,5; 0,5)
Используем формулу перехода к новому основанию логарифма и выносим за скобку общий множитель.
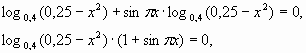
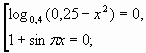 U
U
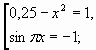 U
U
![]()
Выполним отбор корней, учитывая ОДЗ.
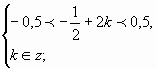 U
U
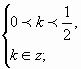 U k I ?
, следовательно,
U k I ?
, следовательно,
уравнение не имеет корней.
Ответ: корней нет.
Пример 1.2. Решить уравнение:
![]() .
.
Решение:
ОДЗ: ![]()
Переходя к основанию (x +1) и преобразуя логарифм степени, имеем
![]()
Разделим обе части уравнения на ![]()
6![]() -
13
-
13![]() + 6 = 0
+ 6 = 0
Пусть ![]() = t,
тогда имеем
= t,
тогда имеем
6t2 -13t + 6 =0, t> 0
Решая квадратное уравнение, находим ![]() ,
,
![]()
Возвращаясь к прежней переменной, получим совокупность
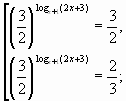 U
U
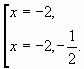
Учитывая ОДЗ, имеем x = ![]() .Ответ:
x =
.Ответ:
x = ![]() .
.
2. Использование экстремальных свойств функции. Метод оценок.
Обоснованием метода оценок является
Теорема №1: "Если на промежутке Х наибольшее
значение функции ![]() равно A
и наименьшее значение функции y = g(x) тоже равно A , то уравнение
равно A
и наименьшее значение функции y = g(x) тоже равно A , то уравнение
![]() = g(x)
равносильно системе уравнений
= g(x)
равносильно системе уравнений ![]()
Применение метода оценок предполагает нахождение наибольшего и наименьшего значений элементарных функций или их "композиций" на заданном множестве, а также использование некоторых "полезных" неравенств:
1. Неравенство Коши. Пусть ![]()
Тогда имеет место ![]() где
k
где
k![]() 2
2
В частности, если k =2, то неравенство Коши принимает вид:
![]() , где
, где
![]() (1)
(1)
2. Неравенство для суммы двух взаимно обратных
чисел ![]() где а
> 0, (2)
где а
> 0, (2)
которое также является следствием неравенства
(1), если допустить, что ![]() .
.
3. Неравенство для разности двух взаимообратных
чисел ![]() , где
а< 0. (3)
, где
а< 0. (3)
4. Неравенство а2 + в2
![]() 2/ав/.
(4)
2/ав/.
(4)
5. Неравенство для суммы синуса и косинуса одного и того же аргумента:
![]() (5)
(5)
Пример 2.1. Решить уравнение:
![]() .
.
Решение:
О.Д.З.: x - любое, кроме ![]()
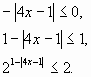
![]()
![]() по
свойству (2).
по
свойству (2).
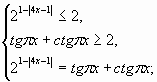
![]()
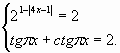
Корень показательного уравнения ![]() является
также корнем тригонометрического уравнения системы (проверяем
подстановкой), следовательно,
является
также корнем тригонометрического уравнения системы (проверяем
подстановкой), следовательно, ![]() -
решение системы и корень исходного уравнения.
-
решение системы и корень исходного уравнения.
Ответ: ![]() .
.
3. Использование свойства монотонности функций.
Для решения комбинированных уравнений с использованием монотонности функций полезно знать следующую теорему:
Теорема № 2. Если функция ![]() -
возрастающая на
-
возрастающая на ![]() ,
функция
,
функция ![]() -
убывающая на
-
убывающая на ![]() , то
уравнение
, то
уравнение ![]() либо не
имеет корней, либо имеет единственный корень на
либо не
имеет корней, либо имеет единственный корень на ![]() .
.
Пример 3.1. Решить уравнение:
![]()
Решение:
О.Д.З.: ![]() .
.
Выполнив преобразования, получим
![]() ,
,
![]() ,
,
![]() .
.
Очевидно, что x = 7 - корень уравнения. Докажем, что других корней нет.
Функция ![]() -
убывает на
-
убывает на ![]() .
.
![]() ,
,
![]()
Если ![]() , то
, то
![]() ,
следовательно
,
следовательно ![]() возрастает
на
возрастает
на ![]() , тогда
по теореме 2 уравнение
, тогда
по теореме 2 уравнение ![]() имеет
единственный корень.
имеет
единственный корень.
Ответ: 7.
Примечание
Методы, рассмотренные в §2; §3 представляют собой две разновидности функционально-графического метода.
4. Применение производной.
Нахождение области значений элементарных функций, входящих в комбинированное уравнение, не всегда возможно осуществить, используя свойство ограниченности их области значений. В таких случаях бывает полезно применить производную для нахождения экстремумов функций.
Пример 4.1. Решить уравнение:
![]()
Решение:
![]()
Пусть ![]() ;
;
![]() .
.
Найдем ![]() -
области значений этих функций.
-
области значений этих функций.
![]() , т.к.
графиком функции
, т.к.
графиком функции ![]() является
парабола с направленными вниз
является
парабола с направленными вниз
ветвями и вершиной в точке (0;1).
![]()
![]()
x = 0 - критическая точка функции ![]()
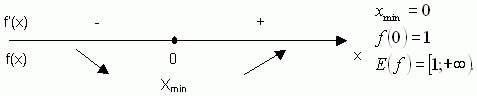
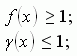
равенство ![]() возможно,
если
возможно,
если
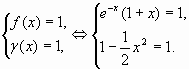
Корень второго уравнения x = 0 подставим в первое уравнение системы, получим верное числовое равенство, следовательно x = 0 - решение системы и корень исходного уравнения.
Ответ: 0.
Решение комбинированных уравнений методом разложения на множители и методом введения новой переменной.
Пример 1.3 Решить уравнение.
(![]() )
)![]()
![]()
Решение:
ОДЗ ![]()
![]()
![]()
Задача сводится к решению совокупности трех уравнений:
![]()
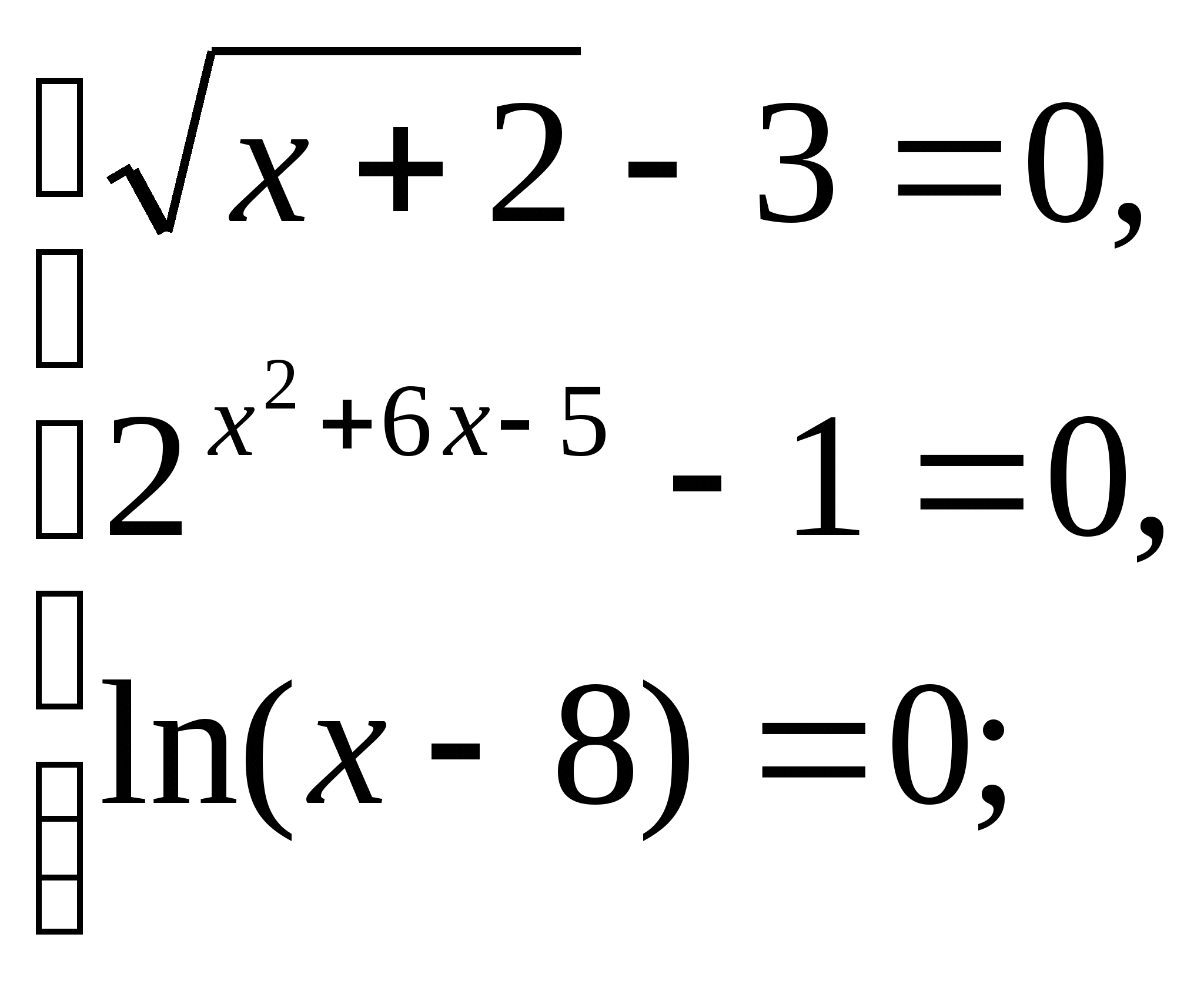
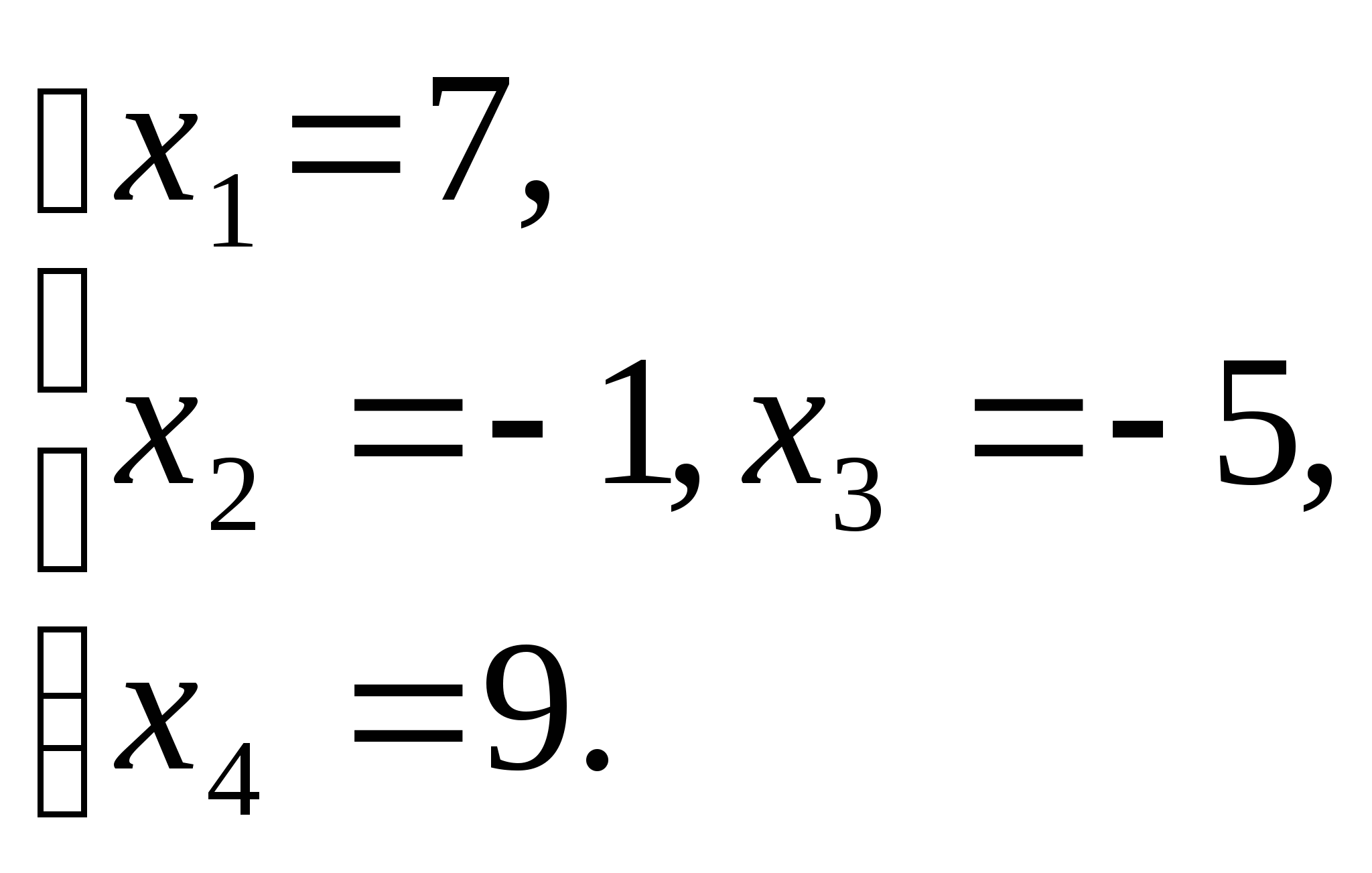
Учитывая ОДЗ, x =9
Ответ: 9
Пример 1.4. Решить уравнение.
![]()
Решение: (x2-x23x) - (9-93x) = 0;
x2-(1-3x) - 9(1-3x) = 0;
(1-3x)(x2-9) =0;
1-3x=0 или x2-9 = 0;
3x=1; x2 =9;
x = 0. x= 3.
Ответ: -3; 0;3
Пример 1.5 Решить уравнение.
![]()
Решение:
О ДЗ:
ДЗ:
![]() x(1;2) (2;+
x(1;2) (2;+![]() )
)
Используя формулу перехода к новому основанию логарифма, получим
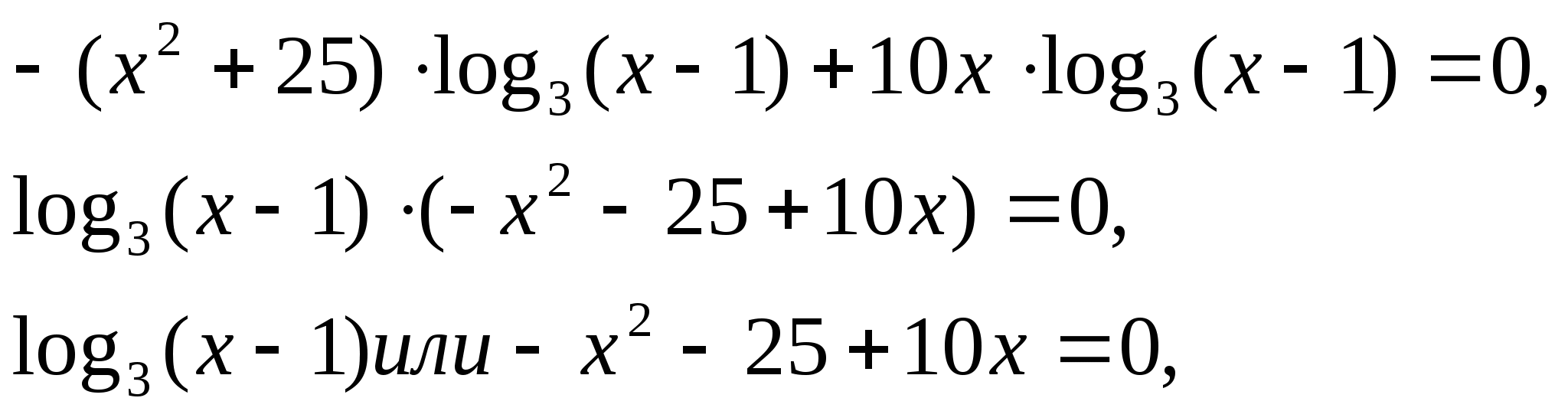
x = 2. x = 5.
Учитывая ОДЗ, x = 5.
Ответ: 5
Пример 1.6. Решить уравнение:
![]() .
.
Решение:
ОДЗ: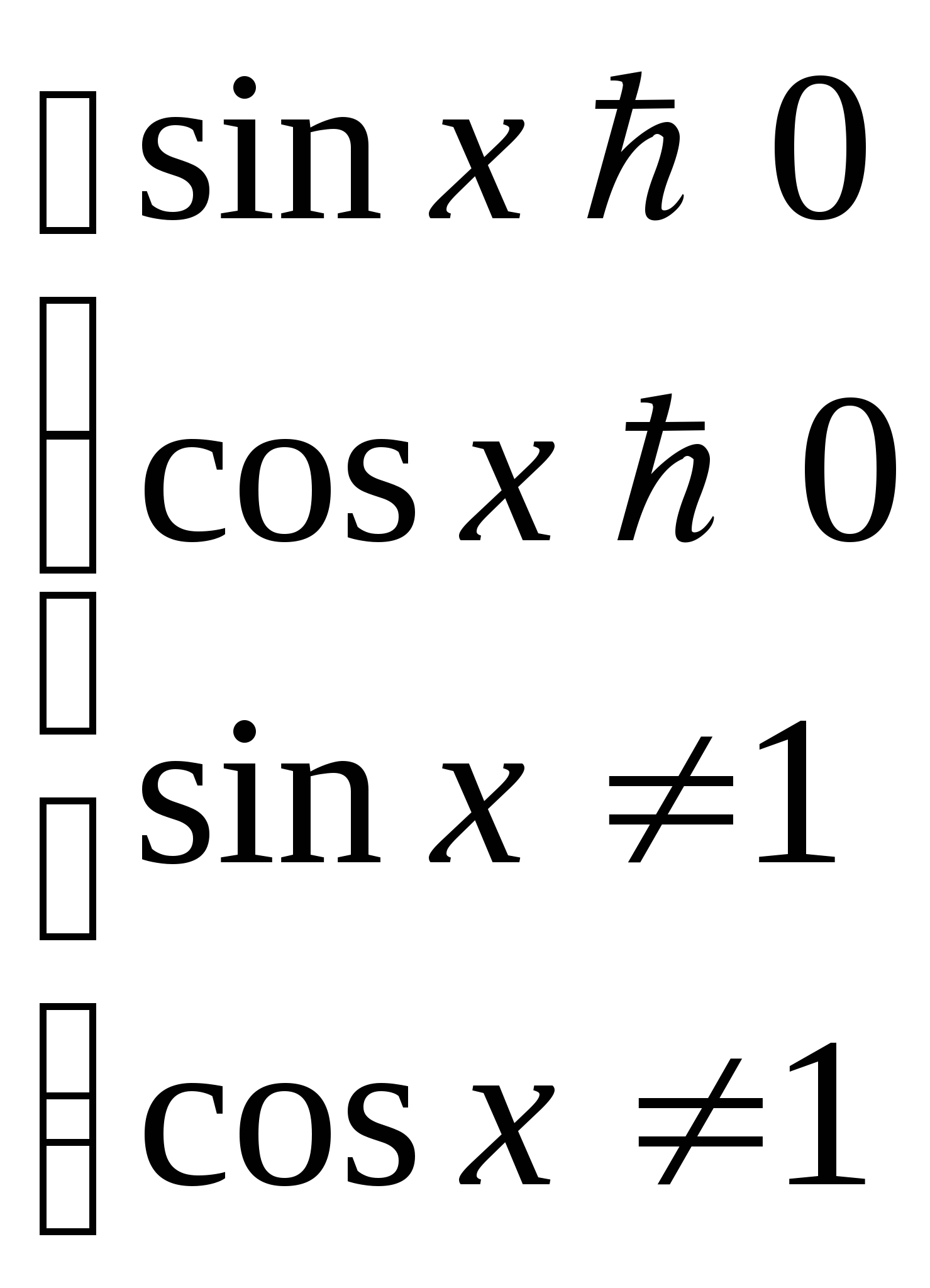
![]()
По формуле перехода к новому основанию логарифма имеем:
![]()
Пусть ![]() , тогда
, тогда
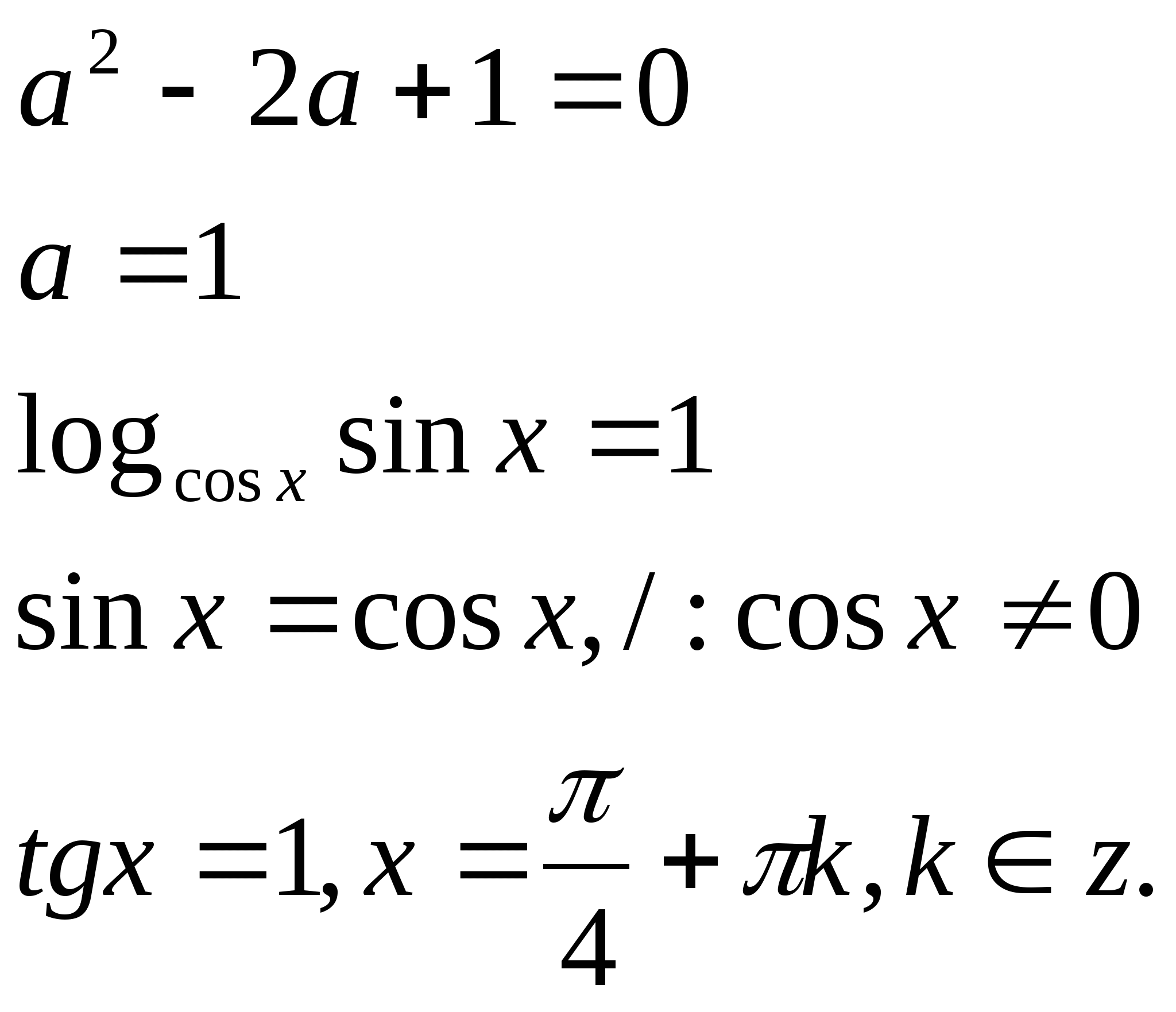
Учитывая ОДЗ, ![]()
Ответ: ![]()
Урок обобщения по теме: "Проценты"
Тип урока: комбинированный урок.
Цель урока: обобщение и систематизация знаний, умений и навыков.
Сегодня мы будем работать по теме: "Сколько нас было и сколько нас стало?". Вы все были участниками большого события, произошедшего в апреле 2002 года. По всей стране прошла перепись населения. Цитата из словаря: "Перепись - это специально организованный периодический или единовременный процесс сбора статистической информации. Проводится одновременно на всей территории по единой программе и методологии. Перепись населения - это получение демографических, экономических, социальных сведений о жителях страны или отдельной территории". Демографическими сведениями называются показатели численности, состава, размещения и изменения населения.
Первые сведения о численности якутов можно найти в книге Вацлава Леопольдовича Серошевского "Якуты". К приходу русских якуты были относительно немногочисленным народом. Вопрос о численности коренных жителей интересовал царское правительство с самого начала. С начала XVIII в. стали появляться расчеты исследователей. Самую кропотливую работу проделал замечательный ученый, этнограф Б. О. Долгих, оставивший фундаментальный труд о расселении и численности всех сибирских народностей XVII в. В основу его расчетов легли подлинные ясачные книги. Вот его данные.
-
Ко времени прихода русских (условно - середина XVII в.) якутов обоего пола было 28470 человек. Это составляло 58,9% от общего числа жителей Якутии. Сколько людей проживало тогда в Якутии?
-
В 1897 г. была проведена Всеобщая перепись населения Российской империи. По данным этой переписи якутов стало 221067 человек. На сколько процентов увеличилось количество коренного народа Якутии?
-
Спустя 30 лет, по Всесоюзной переписи населения 1926 г., было учтено в Якутской АССР 235926 якутов. А численность всего населения составила 287300 человек. Сколько процентов составляли якуты от всего населения?
-
В 1939 году в Якутии проживало 413800 людей. На сколько процентов возросло население по сравнению с 1926 г.?
-
По данным переписи 1959 года население Якутии увеличилось на 17,8% с 1939 г. Вычислите, сколько людей проживало?
-
Вы, наверное, заметили, что за период с 1939 по 1959 гг. прирост населения Якутии меньше, чем за период с 1926 по 1939 гг. Как вы думаете, чем это обусловлено? (В этот период произошли большие демографические потери в годы Великой Отечественной войны).
-
Следующая перепись проводилась в 1989 году. Ее итоги: в Якутии проживает 1081400 человек, 35,3% составляют якуты, 50,9% - русские. Вычислите, сколько якутов и русских проживало тогда в нашей республике?
-
В последней переписи вы участвовали. Она проводилась в апреле 2002 года. Она показала, что количество якутов увеличилась на 16,8%, а численность всего населения Якутии - 948100 человек. Вычислите, сколько нас (якутов) стало и на сколько процентов уменьшилось население.
Теперь, домашнее задание. Я вам предлагаю решить три задачи:
-
Население России по переписи 2002 года составляло 144954200 людей. Только за первое полугодие 2003 года население России уменьшилось на 0,3%. Вычислите, на сколько людей уменьшилось население России.
-
Численность школьников в Российской Федерации уменьшается с каждым годом: в 2000 г. вас (школьников) было 23505000, по прогнозам в 2004 г. число школьников уменьшится на 18,8%. Сколько вас станет в 2004 году?
-
В 2002 году в России детей школьного возраста было 21388000 человек. Узнайте, какой процент от общего числа населения России составляют школьники.
Кроме решения этих задач будет еще одно задание: самим составить задачи по этой теме. Для этого я рекомендую книгу "Экология" из серии "Энциклопедия для детей" издательского центра "Аванта +", том 19. Прочтите внимательно очерки по разделу 3 "Экология человека" и составьте по две задачи.
Учебный проект: экологическое исследование "Автотранспорт и воздух города"
У каждого века вечность вопрошает:
что же свершится в будущем с природой?
А. Кольцов
Качество воздуха - один из важнейших показателей качества окружающей среды, влияющий на здоровье человека, состояние зеленых насаждений, архитектурных сооружений, памятников. Проект является исследовательской деятельностью и подразумевает использование интерактивных методов. Проектно-исследовательская деятельность позволяет школьникам практически применить знания, полученные на уроках математики, биологии, экологии.
При работе по проекту школьникам предлагается изучить транспортную нагрузку на улицах, оценить количество угарного газа, попадающего в окружающую среду с выхлопными газами автомобилей. Предполагается, что на основе полученных данных участники проекта выработают предложения по улучшению экологической ситуации.
Учащимся предложили разделить машины на четыре группы: легковые; грузовые; автобусы ; микроавтобусы. Так же нами была упрощена формула по расчету выброса до следующего вида: M = m . n, где m - количество угарного газа, выбрасываемого одним автомобилем определенного типа, г/км (в этом коэффициенте мы заранее учли влияние среднего возраста автомобилей и технического состояния машин), n - среднее количество автомобилей определенного типа, проехавших за один час, М - масса угарного газа, выбрасываемого автомобилями определенного типа на протяжении одного километра пути.
Цель: формирование экологического сознания и экологической культуры у школьников.
Задачи:
1.Привлечение внимания детей к проблеме
загрязнения атмосферы.
2. Выявление путей решения проблемы загрязнения воздуха.
3. Реализация межпредметных экологических связей.
4. Формирование активной позиции школьников по вопросам защиты
окружающей среды.
5. Развитие коммуникативных способностей ребят.
6. Развитие навыков сотрудничества.
7. Закрепление навыков действий с дробными выражениями, применение
этих действий при решении практических задач.
8. Формирование навыков чтения и составления столбчатых диаграмм.
Этапы экологического исследования
1."Погружение" в проблему. На этом этапе учащиеся знакомятся с одной из глобальных экологических проблем - загрязнением атмосферы. Здесь же ребятам зачитывается письмо от … отд. ГИБДД МО с просьбой провести оценку выбросов автотранспорта, распределяются задания между всеми учениками класса.
2. Организация деятельности
1. Подсчитать количество машин, проезжающих в час по проспекту Красной Армии г. Сергиев Посад и поселку Загорские Дали, разделив их на следующие типы: легковые; грузовые; автобусы, микроавтобусы. Подсчет вести два раза за день: с 10 до 11 часов (время затишья) и с 17 до 18 (час пик).
2. Подготовить плакат с девизом урока и плакаты, иллюстрирующие проблему загрязнения атмосферы, сообщение по теме.
3. Подготовить видеосюжет о состоянии воздуха на исследуемых улицах с опросом общественного мнения.
3. Осуществление деятельности и подведение итогов (презентация результатов)
Заключительный этап проводится в форме внеклассных мероприятий (одно или два занятия, по необходимости), в ходе которых учащиеся завершают выполнение заданий в рабочем листе, формулируют выводы, заполняют экспертную справку. Ученики класса делятся на группы: первая - пр. Красной Армии, вторая - Загорские дали. На доске заготовлены ватманы для составления сравнительных диаграмм, начерчены таблицы, которые заполняют представители групп в ходе занятия.
ХОД ЗАНЯТИЯ
-
Вступительное слово о целях и задачах. Видеосюжет.
-
Сообщение о проблемах, связанных с загрязнением атмосферы.
-
Деятельность по рабочему листу (решение задач, составление диаграмм) .
-
Подведение итогов, обсуждение данных.
-
Составление экспертной справки.
-
Слово в защиту воздуха.
Задания для групп на внеклассном занятии.
Задание 1. Заполнить таблицу (каждая группа по своей улице)
Задание 2. Используя данные таблицы, построить сравнительные диаграммы: выброс угарного газа автомобилями разных типов (для каждой улицы); выброс угарного газа на разных улицах.
Задание 3. Предположить, что весь автотранспорт перевели на газ и любой тип автомобиля выбрасывает в среднем 25 г/км угарного газа. Как изменится состояние воздушной среды? Заполнить таблицу 2 на рабочем листе и достроить диаграммы.
Задание 4 (устно). Ответить на вопросы: на какой из обследованных улиц состояние воздушной среды наиболее благоприятно и почему; сделать вывод об использовании сжатого газа в виде топлива.
Задание 5. Разработать в группах предложения по улучшению качества воздушной среды и заполнить экспертную справку.
Приложения.
Таблица 1.
Ф. И. заполняющих: ______________________
Рабочая формула: М = m . n, где m - количество угарного газа, выбрасываемого одним автомобилем определенного типа (г/км), n - среднее количество автомобилей определенного типа, проехавших за один час.

Экспертная справка о состоянии воздушной среды проспекта Красной Армии и поселка Загорские дали
__________ 2004 год учащиеся ____ класса школы ___________________
1. Результаты расследования (где n - количество автомобилей определенного типа, m - выброс угарного газа одним автомобилем определенного типа, М = m . n)
Элективный курс "Математика и цветоводство"
В современном мире экология как наука приобретает особое значение в связи с усилением воздействия человека на природу. Она уже не может считаться только наукой об отношениях живых организмов с окружающей средой. Задачами экологии на современном этапе являются поиск новых путей сосуществования человека и природы, изучение философских, социальных, экономических, образовательных и других проблем, стоящих перед обществом.
При преподавании школьных предметов имеется возможность продемонстрировать взаимосвязи между понятиями, принятыми в различных областях знаний, и процессами, протекающими в природной среде, в человеческом обществе.
При изучении геометрии в школе можно установить взаимосвязи между геометрическими понятиями и окружающим миром. С древности, наблюдая за окружающей природой и создавая произведения искусства, люди искали закономерности, которые позволяли бы определить прекрасное, т. е. пытались вывести "формулу красоты".
Ряд "формул красоты" известен. Это - правильные геометрические формы: квадрат, круг, равносторонний треугольник и т. д.; это - законы симметрии. Можно привести множество примеров присутствия симметрии в окружающем нас мире. Симметрию легко обнаружить в природных и рукотворных формах. Эстетическое наслаждение, получаемое человеком при наблюдении совершенных форм предмета, объясняется не только выполнением законов симметрии, но и присутствием так называемой "божественной" пропорции, "золотого сечения" в соотношении частей, на которые предмет делится естественным образом. Соблюдение пропорций в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания. "Золотое сечение" являлось критерием гармонии и красоты во времена Пифагора и в эпоху Возрождения. Знания об этом уникальном отношении частей к целому продолжают наполняться новым содержанием, проникая в самые разнообразные области человеческих знаний. Одновременно с этим может быть найден подход к решению одной из задач воспитания экологической культуры - созданию целостной картины мира в сознании школьников.
В связи с вышеизложенным, элективный курс "Математика и цветоводство" ставит следующую цель: показать, как математические понятия взаимосвязаны с окружающей средой, и дать школьникам базовые знания по выращиванию комнатных растений, уходу за ними, по растительному дизайну внутренних помещений.
Задачи:
-
обеспечить педагогические условия для расцвета личности школьника с учётом его возрастных особенностей; развитие творческих сил, способностей и дарований;
-
развивать гуманистические субъект субъектные отношения;
-
формировать основанное на общечеловеческих ценностях и законах красоты мировоззрение учащихся;
-
формировать устойчивый интерес к дисциплинам естественно-математического цикла.
-
способствовать формированию интереса к окружающей природе, среде обитания и мотиваций к познанию через использование математических понятий;
-
способствовать формированию качеств самостоятельности и самоактуализации;
-
научить выращивать и разводить цветы, разрабатывать и выполнять дизайнерские проекты по озеленению отдельных участков внутреннего пространства помещений;
-
способствовать развитию интереса к трудовой деятельности как виду творчества, формированию навыков гигиены и охраны труда при работе с растениями;
В процессе педагогической деятельности задействованы следующие виды обучения: традиционное (объяснительно-иллюстративное) обучение, проблемное (самостоятельное добывание знаний в процессе решения учебных проблем, развитие творческого мышления и познавательной активности учащихся) и инновационное (самообразование, самовоспитание, саморазвитие учащихся посредством самостоятельной работы с информационным и методическим материалами).
Эти виды обучения предполагают следующие формы организации обучения:
-
Индивидуальные, групповые, коллективные формы обучения.
-
Взаимного обучения, самообучения и саморазвития.
-
Массовые мероприятия: экскурсии, творческие отчёты, участие в семинарах, конференциях, выставках и т.п.
Занятия включают в себя теоретическую и практическую части, в зависимости от целесообразности, лекции, консультации, лабораторную работу, опытную работу, самостоятельную работу, творческую проектную работу и т.п.
Эффективность обучения будет отслеживаться следующими формами контроля:
-
самостоятельная работа;
-
срезы знаний, умений в процессе обучения;
-
итоговый контроль.
Показателем эффективности обучения также будут повышающийся интерес к математике, биологии, черчению, творческая активность и результативность учащихся.
Данный элективный курс "Математика и цветоводство" предназначен для школьников 10-11-х классов и рассчитан на 35 часов.
Итоговый контроль предусматривает:
-
в конце первого раздела - проверка первоначальных знаний умений и навыков по комнатному цветоводству. Форма контроля - собеседование;
-
в конце второго раздела - теоретическая подборка материалов по выращиванию цветов одного вида и её защита;
-
в конце третьего раздела - защита воплощённого растительного дизайн проекта оформления избранного участка интерьера школы.
Учебно-тематическое планирование
Из истории растений. Строение растений. "Золотое сечение". Практическая работа по определению "золотого сечения" у растений. Как поливать и подкармливать комнатные растения. Световой и температурный режим. Почва и посуда для комнатных растений. Пересадка и размножение комнатных растений. Болезни и вредители.
Знания и умения: Обучающиеся должны знать, как появились растения, как составляются имена того или иного растения; должны знать строение растения и уметь определять "золотое сечение"; должны научится поливать и подкармливать комнатные растения; уметь правильно регулировать световой и температурный режим; должны знать какие почвы и для какого растения применимы; уметь выполнить пересадку растения; знать и уметь определить заболевание и вредителей комнатного растения.
Раздел II. Особенности выращивания и размножения различных групп комнатных растений.
В этом разделе рассматриваются растения, входящие в семейства: акантовые, амариллисовые, аспарагусовые, асфоделовые, бромеливые, кактусовые, коммелиновые. Отличительные признаки этих семейств. Требования к уходу. Цветение, корни, удобрение, свет, размножение.
Знания и умения: Обучающиеся должны знать отличительные признаки растений, входящих в определённое семейство и уметь по этим признакам классифицировать растения по семействам; знать основные требования к уходу за растениями определённого семейства и уметь ухаживать за ними; уметь определять заболевание и вредителей комнатного растения и уметь их устранять и предотвращать; знать, как размножаются растения того или иного семейства, и уметь это делать.
Раздел III. Цветочный дизайн.
Этот раздел знакомит обучающихся с применением геометрических преобразований (симметрия, зеркальное отображение, поворот) в цветочном дизайне. Построение плана комнаты. Основные понятия и виды дизайна. Цвет, освещение. Как подобрать растения для гостиной, детской комнаты, кухни и ванной комнаты. Разработка дизайнерских проектов этих помещений.
Знания и умения: Обучающиеся должны знать, как и где в комнатном цветоводстве можно применить геометрические понятия; уметь выполнять построение плана комнаты с учётом требований ГОСТа; уметь подобрать комнатные растения с учётом расположения и планировки квартиры для того или иного помещения; уметь составлять дизайнерские проекты гостиной, детской комнаты, кухни и ванной комнаты и осуществлять их.
Литература.
-
Макровская М.М. Уголок природы в детском саду. Москва, Просвещение, 1989г.
-
Клинковская Н.И., Пасечник В.В. Комнатные растения в школе. М, Просвещение, 1986г.
-
Серпухова В.И., Тавлинова Г.К. Комнатные и балконные растения. Ленинградское газетно-журнальное и книжное издательство, 1955г.
-
Гладкий Н.П. Декоративное цветоводство. Л., Колос 1977г.
-
Миско Л.А. Розы. М, Наука 1986г.
-
Степанова И. Лианы. М., "Панорама", 1991г.
-
Николаенко Ц.П. Справочник цветовода М., Колос, 1971г.
-
Горкин А.П., Андреева И.А. Краткая энциклопедия домашнего хозяйства. М., Большая, российская энциклопедия, 1993г.
-
Ракуленко В.В. Декоративное садоводство, М, Просвещение, 1982г.
-
Журнал "Растения в интерьере". М, 2002-2003г.
-
Балашова Е.В., Тищенко М.Н. Библиотечный дизайн, М., Гадарики, 2004г.
-
Журнал "Зелёный интерьер", Издательство Зеркало, 2001г.
-
Журнал "Цветы в доме", Издательство Бурда, 2002-2003г.
-
Чуб В.В., Лезина К.Д. Полная энциклопедия комнатных растений. М.; Изд-во Эксмо, 2002г.
-
Комнатные растения М.; АСТ: Астрель, 2001г.
-
Зонхильд Бишофф, Урсула Копп. Зимний сад. Планирование. Строительство. Выбор растений./Пер. с нем. - М.: БММ АО, 2002г.
-
Журнал "Комнатные и садовые растения" Русское издание итальянского проекта "Verdissimo", выпуск 1-60, 2003-2004г.
-
Александров А.Д. и др. Геометрия 10-11. М.; Просвещение, 1994г.
-
Атанасян Л.С. Геометрия 10-11. М.; Просвещение, 2003г.
-
Газета "Математика" № 42, 2000г.
Элективный курс "Математическая статистика и теория вероятностей"
Современной России нужны люди, способные принимать нестандартные решения, умеющие творчески мыслить, хорошо ориентироваться в обычных житейских ситуациях и повседневной хозяйственной и производственной деятельности.
Введение элементов статистики и теории вероятностей в содержание математического образования является одним из важнейших аспектов модернизации содержания образования, так как роль этих знаний в современном мире повышается.
Цель курса «Математическая статистика и теория вероятностей» состоит в ознакомлении учащихся со случайными величинами и числами, столь необычными для школьников и естественными в повседневной жизни; развитие в них стохастического аспекта представлений об окружающем нас мире.
Задачи курса:
- обеспечить условия для расцвета личности школьника с учетом его возрастных особенностей;
- развитие творческих способностей и дарований;
- формировать устойчивый интерес к изучению математики;
- способствовать формированию качеств самостоятельности и самоактуализации.
В процессе обучения учащиеся узнают:
- место статистики в изучении окружающего мира;
- природу и механизм возникновения случайных величин;
- основные понятия математической статистики;
- суть критериев статистической проверки гипотез.
Умеют:
- строить законы распределения случайных величин;
- вычислять математическое ожидание и дисперсию и их точечные и интервальные оценки;
- проверять гипотезы о среднем и дисперсии;
- решать комбинаторные задачи.
При обучении статистике можно использовать стохастические игры, статистические исследования, эксперименты со случайными исходами, мысленные статистические эксперименты и моделирование.
В процессе изучения материала используются как традиционные формы обучения, так и самообразование, саморазвитие учащихся посредством самостоятельной работы с информационным и методическим материалом.
Предполагаются следующие формы организации обучения:
- индивидуальная, групповая, коллективная;
- взаимное обучение, самообучение, саморазвитие.
Занятия включают в себя теоретическую и практическую части, в зависимости от целесообразности - лекции, консультации, самостоятельную работу, творческую проектную работу и т.п.
Эффективность обучения отслеживается следующими формами контроля:
- самостоятельная работа;
- срезы знаний, умений в процессе обучения;
- итоговый контроль.
Показателем эффективности обучения следует считать повышающийся интерес к математике, творческую активность и результативность учащихся.
Динамика интереса отслеживается с помощью анкетирования на первом и последнем занятиях, собеседования в процессе работы после выполнения каждого вида обязательных работ.
Итоговый контроль предусматривает:
I раздел - творческая подборка вероятностных задач и их защита.
II раздел - собеседование.
III раздел - написание и защита рефератов.
Данный элективный курс «Математическая статистика и теория вероятностей» составлен на основе программы для школ с углубленным изучением математики, авт. Н.Я. Виленкин.. Предназначен для учащихся 10-11 классов и рассчитан на 34 часа.
Содержание курса
«Математическая статистика и теория вероятностей»
Раздел I. Статистика и вероятность (18 ч.).
Табличные и графическое представление информации; гистограммы выборок.
Поочередной и одновременный выбор нескольких элементов из конечного множества; решение комбинаторных задач.
Вероятностное пространство как модель реального эксперимента; элементарные исходы и случайные события; различные определения вероятности; формулы для числа перестановок, размещений и сочетаний; биноминальные коэффициенты, треугольник Паскаля и его свойства.
Классический способ нахождения вероятности случайных событий; правило сложения вероятностей; геометрические вероятности; условная вероятность; два подхода к определению условной вероятности; правила умножения вероятностей.
Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события; вероятность и статистическая частота наступления события; формула полной вероятности.
Раздел II. Основные понятия математической статистики (9 ч.).
Место статистики в изучении окружающего мира.
Случайные величины и их природа.
Статистическая вероятность.
Выборки и выборные функции.
Числовая выборка как реализация случайной величины.
Представление результатов выборки в частотных таблицах.
Дискретные и непрерывные признаки.
Закон распределения случайной величины. числовые характеристики случайных величин: математическое ожидание, мода, медиана, размах, дисперсия, стандартное отклонение.
Испытания Бернулли. формула Бернулли и биномиальное распределение.
Раздел III. Статистическое оценивание и прогноз (7 ч.).
Точечные и интервальные оценки характеристик выборки.
Методы построения оценок и вычисления их погрешностей.
Оценка вероятности события по его частоте.
Определение наиболее вероятного исхода случайного эксперимента.
Проверка гипотез: уровень значимости, ошибки первого и второго рода.
Какие события можно считать маловероятными?
В результате прохождения курса обучающиеся умеют:
решать комбинаторные задачи изученных типов;
вычислять вероятность события, пользуясь простейшими свойствами вероятности;
использовать статистические инструменты для анализа данных;
строить законы распределения случайных величин;
проверять гипотезы о среднем и дисперсии;
знают:
место статистики в изучении окружающего мира;
природу и механизм возникновения случайных величин;
основные понятия математической статистики;
суть критериев статистической проверки гипотез;
формулы для подсчета числа размещений, перестановок, сочетаний;
биноминальные коэффициенты.
Учебно-тематическое планирование материалаКоличество
часов
1
2
3
4
5
6
7
8
9
1
2
3
4
5
1
2
3
4
Раздел I. Статистика и вероятность (18 ч.).
Табличное и графическое представление информации.
Гистограммы выборок.
Поочередной и одновременный выбор нескольких элементов
из конечного множества.
Решение комбинаторных задач.
Вероятностное пространство.
Формулы для числа перестановок, размещений, сочетаний.
Схема Бернулли.
Вероятность случайных событий.
Условная вероятность. Независимость событий и испытаний.
Вероятность и статистическая частота наступления события.
Раздел II. Основные понятия математической статистики (9 ч.).
Случайные величины и их природа.
Статистическая вероятность.
Законы распределения случайных величин.
Выборки и выборные функции.
Формула Бернулли.
Раздел III. Статистическое оценивание и прогноз (7 ч.).
Методы построения оценок.
Оценка вероятности события по его частоте.
Проверка гипотез.
Итоговое занятие.
2
2
2
4
2
1
2
2
1
1
2
2
2
2
2
2
2
1
Литература
Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика. - М., 1973.
Пугачев В.С. Теория вероятностей и математическая статистика. - М., 1979.
Четыркин Е.М., Калахман И.Л. Вероятность и статистика. - М., 1982.
Мордкович А.Г., Семенов П.В. События. Вероятность. Статистика: Дополнительные материалы к курсу алгебры для 7 - 9 кл. - М.:Мнемозина, 2002. (к учебникам А.Г. Мордковича)
Ткачева М.В.,Федорова Н.Е. Алгебра, 7 - 9: Элементы статистики и вероятность. - М.: Просвещение, 2003. (к учебникам А.Ш. Алимова и др.)