Технологическая карта урока ' Решение квадратных уравнений с параметрами' 8 класс.

Технологическая карта урока в соответствии

с требованиями ФГОС.

Автор: Толмачева Лариса Анатольевна, учитель математики МБОУ Заворонежской СОШ, Мичуринский район, Тамбовская обл.

Предмет: математика.

Класс: 8 класс.

Тема урока: решение квадратных уравнений с параметрами.

Тип урока: комбинированный.

Планируемые результаты обучения:

• личностные: логичность мышления, умение работать в проблемной ситуации;

• предметные: формировать умение решать квадратные уравнения с параметром;

• метапредметные: формирование информационной, коммуникативной и учебной компетентности учащихся, умения работать с имеющейся информацией в новой ситуации.

Техники и технологии: системно-деятельностное бучение, проблемное обучение, ИКТ.

Ресурс ( учебники, наглядные пособия. ИКТ) учебник Авторы: Макарычев Ю.Н. Издание: М.: Просвещение, 2013

Этапы урока (время)

Деятельность учителя

Деятельность учащихся

Формируемые УУД

Формы оценивания

Личностные

Регулятив-ные

Коммуни-ка­тивные

Познава-тель­ные

1. Организационный момент.

(2 мин)

Приветствует учащихся, организует рабочее место,

выявляются отсутствующие.

Учащиеся настраиваются на работу.

Волевая саморегуляция

2. Актуали-зация теоретических знаний.

(3мин)

Проводится опрос по теории

Предыдущего урока.

- Какое уравнение называется квадратным?

- Квадратным или линейным является уравнение

а) при b=6; б)0; в) b=0,5;

г) b=5?

-Какое квадратное уравнение называется приведенным?

-Какое выражение называют дискриминантом?

-Сколько корней может иметь квадратное уравнение? (формулы).

-Теорема Виета и обратное утверждение.(записать)

Учащиеся предлагают различные варианты решения, говорят о трудностях, которые у них возникли.

Формировать личную мотивацию к учению.

Целеполагание

Структурировать знания по данной теме

Учебное сотрудничество с учителем

Самооценка формулировок

и формул.

3. Объяснение нового материа-ла.

( 3мин)

При решении квадратного уравнения с параметрами контрольными будут те значения параметра, при которых коэффициент при обращается в 0. Дело в том, что если этот коэффициент равен 0, то уравнение превращается в линейное и решается по соответствующему алгоритму; если же этот коэффициент отличен от нуля, то имеем квадратное уравнение, которое решается по иному алгоритму. Дальнейшее решение зависит от D.

Учащиеся формулируют цель урока: «Научиться решать уравнения с параметром».

Взаимоконтроль и самоконтроль

Умение структурировать знания

Учебное сотрудничество с учителем и сверстниками, управление поведением партнера

4. Приме-нение знаний и умений в новой ситуации

(17 мин)

Объяснение учителя.

Пример 1.

Решить уравнение

Решение: Здесь коэффициент перед отличен от , значит, данное уравнение при любых значениях параметра является квадратным. Найдем дискриминант:

D=

D, значит, квадратное уравнение имеет два различных корня.

p+2 и p-1

Ответ: при любых значениях р p+2 ; p-1.

Пример 2. Решить уравнение p.

Решение: Мы не можем утверждать, что данное уравнение является квадратным. Рассмотрим контрольное значение р=0, имеем два случая.

Если р=0, то получается уравнение вида 0+ х=1.

Если р≠0. То уравнение является квадратным, можно применять формулу D=-

4р(-1)=1-2р++4р=; ; .

Ответ: при р=0 х=1, при р≠0 ; .

Пример 3. Решить уравнение

(а-1)х²+2(2а+1)х+(4а+3)=0.

Найдем значения параметра, обращающие в нуль коэффициент при х

а-1=0 а=1

Решим уравнение при а=1

0х²+2(21+1)х+41+3=0 6х+7=0 .

Найдем значения параметра, обращающие в нуль дискриминант уравнения

D=(2(2а+1))²-4(а-1)(4а+3)=(4а+1)²-(4а-4)(4а+3)=4(5а+4)

4(5а+4)=0 .

Решим уравнение при , в этом случае уравнение будет иметь один действительный корень

9х²+6х+1=0 (3х+1)²=0 .

Решим уравнение при а1, . В этом случае D<0, поэтому уравнение действительных корней не имеет.

Решим уравнение при а1, . В этом случае уравнение имеет два действительных корня

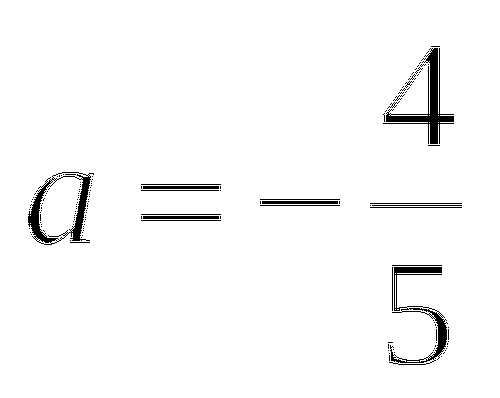
Ответ: 1) при , ;

2) при а=1, ;

3) при , действительных корней нет;

4) при и а1, .

Пример 4. При каких значениях mровно один из корней уравнения

равен 0.

Решение: Если нуль является корнем уравнения, значит квадратный трехчлен =0 обращается в нуль. =-3, =3.

Найдем второй корень при найденных значениях m.

Если m=3, то получаем =0, =-6.

Если m=-3, то получаем =0, которое имеет два кратных корня равных 0.

Ответ при m=3.

5. Закрепле-ние матери-ала

(15мин)

Работа в группах.

Решите уравнение:

( а + 1 ) х ² - 2 ( а + 9 ) х + 9 = 0;

х ² - ( а ² - 5 а) х + 5 а - 1 = 0;

( с - 1) х ² + ( с + 4 ) х + с + 7 = 0;

С последующей проверкой.

Работа в группах. Проблемный диалог. Задают и отвечают на вопросы.

Контроль, коррекция, оценка

Учебное сотрудничество с учителем и сверстниками, управление поведением партнера

Самостоятельная работа.

6. Домаш-нее задание.

(2мин)

1.При каких значениях а уравнение (а+2) +2(а+2)х+2=0 имеет один корень?

2.Решить уравнение .

3. Решить уравнение

4. Решить уравнение ( 2-b-6) = 4(b+1)x-2.

Объясняет какие номера обязательные и какие можно взять по выбору.

Учащиеся записывают домашнее задание и определяют для себя уровни заданий.

Планирование

Постановка вопросов

7. Итог урока. (1мин)

Какие цели стояли на уроке?

Достиг ли каждый из вас цели урока?

Фиксирую проблемы для следующего урока.

Самостоятельно определяют насколько достигнуты цели урока.

Формировать адекватную самооценку.

Формировать умения планировать свою работу.

Формулировать собственное мнение и аргументировать его.

Формулировать познавательную цель.

8. Рефлек-сия

(2 мин)

Учащимся предлагается по желанию продолжить предложение:

На уроке я научился (научилась) …

На уроке мне понравилось …

На уроке мне пригодились знания….

Для меня было сложно…

С урока я ухожу с … настроением!

Учащиеся продолжают предложения.

Прощаются

Смыслообразование, формирование положительного отношения к процессу познания

Оценка- выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.

Рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.