Урок по алгебре Квадратные уравнения (8 класс)

Анферова Гульнара Мавруровна, учитель математики.

Обобщающий урок в 8 классе по теме "Квадратные уравнения"

Цель урока:

• Образовательная: закрепление и обобщение знаний учащихся полученные при изучении темы. Выработка умений и навыков по решению квадратных уравнений различного вида разными способами. Выработка умения выбрать нужный рациональный способ решения.

• Развивающие: развитие логического мышления, памяти, внимания, умений сравнивать и обобщать, умения выступать с самостоятельными суждениями и отстаивать их.

• Воспитательные: воспитание трудолюбия, взаимопомощи, математической культуры. Умение работать в группах, развивать познавательную активность и логическое мышление учащихся, развитие интереса к предмету.

Тип урока: Урок обобщения и систематизации.

Ход урока

I. Организационный момент: сообщение темы и цели урока.

На протяжении многих уроков мы рассматривали квадратные уравнения и методы их решения. На этом уроке мы повторим и закрепим знания и умения решения квадратных уравнений различными способами. Каждый из вас должен уметь правильно, быстро и рационально решать квадратные уравнения. Эта тема очень важна в курсе математики, она является первой ступенькой в изучении более сложного материала. Вам дан ключ к решению квадратных уравнений, и если вы научились ими пользоваться, вы сможете решать любое квадратное уравнение. А сегодня вы покажите, насколько готовы пользоваться этим ключом.

II. Устно:

Вопросы:

1. Какое уравнение называется квадратным?

Ответ: Квадратным уравнением называется уравнение вида x - переменная, а, b, с- некоторые числа. Числа а, b, с называются коэффициентами квадратного уравнения. Число a называют первым коэффициентом, число b- вторым коэффициентом, число с- свободным членом.

2. Какие уравнения называются неполными квадратными уравнениями?

Ответ: Уравнения называются неполными квадратными уравнениями если b = 0 или с = 0.

3. Какое квадратное уравнение называется приведенным?

Ответ: Квадратное уравнение называют приведенным, если его старший коэффициент равен 1; Квадратное уравнение называют не приведённым, если старший коэффициент отличен от 1.

4. Что называют корнем квадратного уравнения?

Ответ: Корнем квадратного уравнения называют всякое значение переменной х, при котором квадратный трёхчлен обращается в нуль. Такое значение переменной х называют также корнем квадратного трёхчлена.

5. Что значит решить квадратное уравнение?

Ответ: Решить квадратное уравнение - значит найти все его корни или установить, что корней нет.

6. Что определяют по дискриминанту квадратного уравнения?

Ответ: По дискриминанту квадратного уравнения определяют, сколько оно имеет корней.

Формулы:

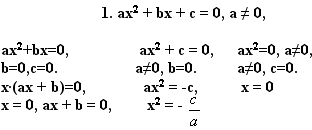
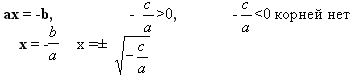
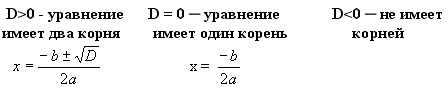
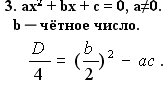
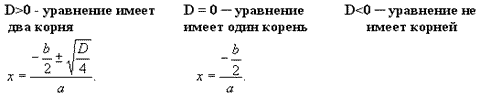
Теорема Виета.

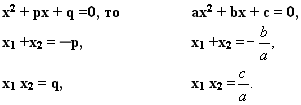
Задания для устной работы:

1.Задание на определение вида уравнения.

Ребята, здесь вы видите уравнения определенные по какому-то признаку. Как вы думаете, какое из уравнений каждой группы лишнее.

Ответ:

А: 3- лишнее, т.к. это полное квадратное уравнение, а 1;2;3-неполные квадратные уравнения.

Б: 2-лишнее, т.к. это уравнение общего вида, а 1;2;3- приведенные квадратные уравнения.

2. Не решая уравнения, найдите корни:

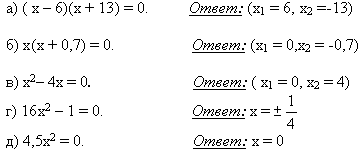
3. Какие из уравнений не имеют корней.

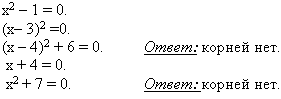
4. Не решая уравнение . Найдите:

5. Найдите сумму и произведение корней в следующих уравнениях

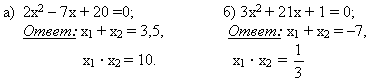
6. Ребята, посмотрите на эти уравнения и их корни. Попробуйте найти закономерность:

а) в корнях этих уравнений;

б) в соответствии между отдельными коэффициентами и их корнями;

в) в сумме коэффициентов.

Ответ:

а) что один из корней равен 1.

б) второй равен g или

в) сумма коэффициентов равна 0.

7. Сформулируйте правило?

Если в уравнении aх² + bх + с = 0 сумма коэффициентов a + b + c = 0,

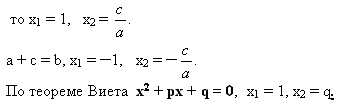
8. Способы решения квадратных уравнений

• Выделения квадрата двучлена.

• По формуле корней.

• С помощью теоремы Виета..

IV. Работа в классе.

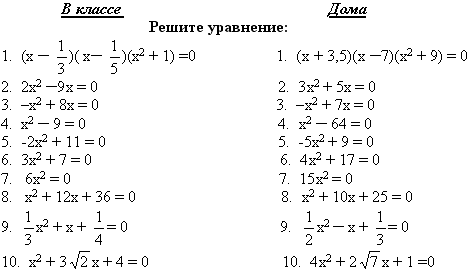
Составьте квадратное уравнение, корнями которого являются числа

Используя теорему Виета и утверждение a + b + c = 0,

найдите корень уравнения:

12. 13х² + 18х - 31 = 0 12. 5х² -27х + 22 = 0

13. Из пункта А одновременно выехали грузовой и легковой автомобили, один на север, другой на восток. Скорость легкового автомобиля на 20 км/ч больше скорости грузового. Через 1,5 ч расстояние между ними составило 150 км. Найдите скорости автомобилей.

V. Тест: "Квадратные уравнения. Теорема Виета"

1 вариант

1. Дискриминант какого из уравнений равен 121?

а) 3х² -5х + 4 = 0; б) 3х² +5х - 8 = 0; в) х² -11х + 1 = 0; г) -3х² - 11х - 8 = 0.

2. Решите уравнение: х² - 8х + 7 = 0.

а) -1; 7; б) 1; -7; в) 1; 7; г) -1; ?7.

3. Найдите сумму корней уравнения: 4х² + 22х - 7 = 0.

а) -22; б) корней нет; в) 22; г) -5,5.

4. Найдите произведение корней уравнения: 5х² - 2х + 9 = 0.

а) 9; б) ?9; в) корней нет; г) 1,8.

5. Выделите квадрат двучлена из многочлена: х² -8х - 11.

а) (х - 8)² - 5; б) (х - 3)² + х; в) (х - 4)² - 5; г) (х - 4)² - 27.

2 вариант

1. Дискриминант какого из уравнений равен 25?

а) 2х² +7х + 3 = 0; б) -2х² +7х + 3 = 0; в) х² -5х + 1 = 0; г) -2х² - 7х + 3 = 0.

2. Решите уравнение: х² - 5х - 36 = 0.

а) 4; -9; б) -4; 9; в) 4; 9; г) -4; -9.

3. Найдите сумму корней уравнения: 5х² - 13х + 9 = 0.

а) 13; б) -13; в) корней нет; г) 2,6.

4. Найдите произведение корней уравнения: 3х² - 7х - 8 = 0.

а) -8; б) 2 в) корней нет; г) 8.

5. Выделите квадрат двучлена из многочлена: х² +10х - 14.

а) (х - 10)² - 6; б) (х + 6)² - 22х; в) (х + 4)² - 39; г) (х + 5)² - 24.

Ответ: