- Учителю
- Методические рекомендации по выполнению самостоятельной работы по математике
Методические рекомендации по выполнению самостоятельной работы по математике
Министерство образования и науки Самарской области
Государственное автономное профессиональное образовательное учреждение
Самарской области
«Тольяттинский индустриально-педагогический колледж»
(ГАПОУ СО «ТИПК»)
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО
МАТЕМАТИКЕ
для студентов специальности
22.02.06 Сварочное производство
Тольятти 2016
Содержание
Введение
Раздел 1.
работа с конспектом лекции
Раздел 2.
составле ние таблиц для систематизации учебного материала
Раздел 3.
работа над материалом учебника
Раздел 4.
подготовка реферата
Раздел 5.
решение задач и упражнений по образцу
Раздел 6.
решение вариативных задач и упражнений
Раздел 7.
выполнение моделей для демонстрации теорем
Раздел 8.
подготовка доклада
Раздел 9.
выполнение чертежей
Раздел 10.
исследовательская работа
Раздел 11.
выполнение моделей пространственных фигур
Заключение
Список литературы
Приложения
Введение
Основная задача среднего профессионального образования заключается в формировании творческой личности специалиста, способного к саморазвитию, самообразованию, инновационной деятельности. Решение этой задачи вряд ли возможно только путем передачи знаний в готовом виде от преподавателя к студенту. Необходимо перевести студента из пассивного потребителя знаний в активного их творца, умеющего сформулировать проблему, проанализировать пути ее решения, найти оптимальный результат и доказать его правильность. В этом плане следует признать, что самостоятельная работа студентов (СРС) является важной формой образовательного процесса.
В первую очередь необходимо достаточно четко определить, что же такое самостоятельная работа студентов.
Самостоятельная работа студентов - это работа, которая выполняется ими по заданию преподавателя, без его непосредственного участия (но под его руководством) в специально представленное для этого время.
Цели самостоятельной работы:
-
качественное усвоение учебного материала;
-
выработка умений и навыков учебной деятельности;
-
формирование познавательных способностей и интереса к изучаемому материалу;
-
формирование готовности к самообразованию;
-
формирование самостоятельности как качества личности.
Классификация самостоятельных работ:
▪ по дидактическим целям:
Обучающие. Такие работы проводятся на этапе подготовки к введению нового материала, т.е. сразу после объяснения. Содержание таких работ составляется из заданий репродуктивного характера, работы проверяются немедленно. Самостоятельно давая ответы на вопросы, студенты осмысливают объяснение преподавателя, запоминают основные свойства, правила, учатся их применять, с интересом воспринимают изучаемый материал, так как сами участвуют в его объяснении. К обучающим самостоятельным работам относятся также самостоятельное составление алгоритмов и решение задач по алгоритму.
Тренировочные. К тренировочным работам относятся задания на распознавание различных объектов и их свойств. В заданиях такого типа часто требуется воспроизвести или непосредственно применить теоремы, определения, свойства тех или иных математических объектов. Тренировочные самостоятельные работы состоят из однотипных заданий, содержащих существенные признаки и свойства данного определения, правила.
Закрепляющие. К таким самостоятельным работам можно отнести те, которые способствуют развитию логического мышления и требуют комбинированного применения различных правил и теорем. Они показывают, насколько прочно, осмысленно усвоен учебный материал.
Повторяющие, развивающие, контролирующие.
▪ по уровню самостоятельности студентов - самостоятельные работы по образцу, реконструктивно - вариативные, частично - поисковые, исследовательские.
По образцу используются при первичном закреплении изученного. В этом случае студенты не выходят за рамки воспроизводящей деятельности, которая направлена на овладение основными знаниями, умениями, способами работы. Предлагаемые при этом задания выполняются по образцам и алгоритмам, показанным преподавателем или подробно описанным в учебнике.
Реконструктивно - вариативные содержат в себе задачи, по условиям которых студентам приходится анализировать новые для них ситуации, переформулировать их, выбирать из известных способов наиболее рациональные.
Частично - поисковые требуют переноса знаний и умений в необычные, нестандартные ситуации.
Исследовательские предназначены для открытия новых сведений об изучаемых объектах, используя накопленные знания и умения, выдвигая и проверяя собственные гипотезы и суждения.
▪ по степени индивидуализации - групповые и индивидуальные.
▪ по источнику и методу приобретения знаний - работа с книгой, решение и составление задач, лабораторные и практические работы, подготовка докладов и т.д.
▪ по форме выполнения - устные и письменные.
▪ по месту - классные и домашние.
Результаты самостоятельной работы
-
обучающий - накопление фактического материала и опыта его личностного осмысления и оценки;
-
развивающий - формирование умений и навыков самостоятельного труда;
-
воспитательный - воспитание добросовестности, усидчивости, прилежания, дисциплинированности, ответственности и др.;
-
диагностический - проявляет истинную картину усвоения обучаемым знаний, умений, навыков, развития их интеллектуальных и физических сил и способностей.
Этапы занятия
Виды самостоятельной работы
Подготовка к восприятию нового материала.
§ предварительное наблюдение;
§ предварительное чтение книги;
§ просмотр рисунков, чертежей, схем;
§ подготовка ответов на заданные учителем вопросы.
Изучение новых знаний.
при объяснении преподавателем нового материала (до объяснения заранее дать задание):
§ составить план;
§ сделать конспект;
§ графически изобразить.
самостоятельно:
§ работа с учебником (выделение главного, определение понятия, отбор материала, проведение сравнительного анализа, поиск ответов на вопросы учителя и т. д.);
§ работа с использованием дополнительных источников: статей, схем, таблиц и т.д.;
§ изучение всей темы по учебнику;
§ наблюдения, опыты.
Применение знаний.
§ упражнения (от выполнения по образцу к более высокому уровню решения и составления задач);
§ сочинения, доклады и т.д.
Обобщение и систематизация знаний.
§ составление сводных таблиц, схем и диаграмм;
§ определение выводов.
Проверка знаний, умений и навыков.
§ работы (письменные, графические, практические) ;
§ тесты;
§ ответы на вопросы преподавателя:
¶ на сравнение, объяснение, доказательство, обоснование
¶ требующие характеристики явлений, оценки предметов
¶ вопросы, требующие анализа, синтеза каких-либо данных.
Организация внеаудиторной самостоятельной работы.
В последнее время число аудиторных часов, выделенных на изучение математики в учреждениях среднего профессионального образования, сокращено, при этом содержательная часть не уменьшилась, а в некоторых разделах даже расширилась. В связи с этим в образовательных стандартах для СПО значительно увеличены нормативы времени на самостоятельную работу студентов. При разработке рабочего учебного плана по дисциплине преподавателем планируется и содержание внеаудиторной самостоятельной работы. При этом необходимо организовать самостоятельную работу таким образом, чтобы каждый студент имел возможность овладеть математическими знаниями и умениями.
Перед выполнением студентами внеаудиторной самостоятельной работы преподаватель проводит инструктаж по выполнению задания, который включает цель задания, его содержание, сроки выполнения, ориентировочный объем работы, основные требования к результатам работы, критерии оценки. В процессе инструктажа преподаватель предупреждает студентов о возможных типичных ошибках, встречающихся при выполнении задания. Инструктаж проводится преподавателем за счет объема времени, отведенного на изучение дисциплины.
Во время выполнения студентами внеаудиторной самостоятельной работы и при необходимости преподаватель может проводить консультации за счет общего бюджета времени, отведенного на консультации.
Самостоятельная работа может осуществляться индивидуально или группами студентов в зависимости от цели, объема, конкретной тематики самостоятельной работы, уровня сложности, уровня умений студентов.
Контроль результатов внеаудиторной самостоятельной работы студентов может осуществляться в пределах времени, отведенного на обязательные учебные занятия по дисциплине и внеаудиторную самостоятельную работу студентов по дисциплине, может проходить в письменной, устной или смешанной форме.
В качестве форм и методов контроля внеаудиторной самостоятельной работы студентов могут быть использованы семинарские занятия, зачеты, тестирование, самоотчеты и др.
Критериями оценки результатов внеаудиторной самостоятельной работы студента являются:
- уровень освоения студентом учебного материала;
- умение студента использовать теоретические знания при выполнении практических задач;
- сформированность общеучебных умений;
- обоснованность и четкость изложения ответа;
- оформление материала в соответствии с требованиями.
Раздел 1. Работа с конспектом лекции
Конспект (от лат. Conspectus - обзор) является письменным текстом, в котором кратко и последовательно изложено содержание основного источника информации. Конспектировать - значит приводить к некоему порядку сведения, почерпнутые из оригинала. В основе процесса лежит систематизация прочитанного или услышанного. Записи могут делаться как в виде точных выдержек, цитат, так и в форме свободной подачи смысла. Манера написания конспекта, как правило, близка к стилю первоисточника. Если конспект составлен правильно, он должен отражать логику и смысловую связь записываемой информации. Им запросто можно воспользоваться через некоторое количество времени, а так же предоставить для применения кому-то еще, поскольку прочтение грамотно зафиксированных данных никогда не вызовет затруднений. «Умный» конспект помогает воспринимать информацию практически любой сложности, предварительно придавая ей понятный вид. В процессе учебы или при решении какой-то задачи в общем объеме информации мы выделяем самое важное и необходимое, вносим в конспект, таким образом, упрощая овладение материалом. В хорошо сделанных записях можно с легкостью обнаружить специализированную терминологию, понятно растолкованную и четко выделенную для запоминания значений различных слов. Используя законспектированные сведения, легче создавать значимые творческие или научные работы, различные рефераты и статьи.
Виды конспектов
Нужно уметь различать конспекты и правильно использовать ту категорию, которая лучше всего подходит для выполняемой работы. ПЛАНОВЫЙ. Такой вид изложения на бумаге создается на основе заранее составленного плана материала, состоит из определенного количества пунктов (с заголовками) и подпунктов. В процессе конспектирования каждый заголовок раскрывается - дополняется коротким текстом, в конечном итоге получается стройный план-конспект. Именно такой вариант больше всего подходит для срочной подготовки к публичному выступлению или семинару. Естественно, чем последовательнее будет план (его пункты должны максимально раскрывать содержание), тем связаннее и полноценнее будет ваш доклад. Специалисты рекомендуют наполнять плановый конспект пометками, в которых будут указаны все используемые вами источники, т. к. со временем трудно восстановить их по памяти. СХЕМАТИЧЕСКИЙ ПЛАНОВЫЙ. Эта разновидность конспекта выглядит так: все пункты плана представлены в виде вопросительных предложений, на которые нужно дать ответ. Изучая материал, вы вносите короткие пометки (2-3 предложения) под каждый пункт вопроса. Такой конспект отражает структуру и внутреннюю взаимосвязь всех сведений и способствует хорошему усвоению информации. ТЕКСТУАЛЬНЫЙ. Подобная форма изложения насыщеннее других и составляется из отрывков и цитат самого источника. К текстуальному конспекту можно легко присоединить план, либо наполнить его различными тезисами и терминами. Он лучше всего подходит тем, кто изучает науку или литературу, где цитаты авторов всегда важны. Однако такой конспект составить непросто. Нужно уметь правильно отделять наиболее значимые цитаты таким образом, чтобы в итоге они дали представление о материале в целом. ТЕМАТИЧЕСКИЙ. Такой способ записи информации существенно отличается от других. Суть его - в освещении какого-нибудь определенного вопроса; при этом используется не один источник, а несколько. Содержание каждого материала не отражается, ведь цель не в этом. Тематический конспект помогает лучше других анализировать заданную тему, раскрывать поставленные вопросы и изучать их с разных сторон. Однако будьте готовы к тому, что придется переработать немало литературы для полноты и целостности картины, только в этом случае изложение будет обладать всеми достоинствами. СВОБОДНЫЙ. Этот вид конспекта предназначен для тех, кто умеет использовать сразу несколько способов работы с материалом. В нем может содержаться что угодно - выписки, цитаты, план и множество тезисов. Вам потребуется умение быстро и лаконично излагать собственную мысль, работать с планом, авторскими цитатами. Считается, что подобное фиксирование сведений является наиболее целостным и полновесным.
Техника составления конспекта
Если вы хотите извлечь максимальную пользу при работе с книгами и учебными пособиями, необходимо учесть следующие моменты.
-
Предварительно просмотрите материал. Так вы сумеете выявить особенности текста, его характер, понять, сложен ли он, содержит ли незнакомые вам термины. При беглом знакомстве с литературой вы сумеете выбрать подходящую разновидность конспектирования.
-
Снова прочтите текст и тщательно проанализируете его. Такая работа с материалом даст вам возможность отделить главное от второстепенного, разделить информацию на составляющие части, расположить ее в нужном порядке. Используйте закладки - это отменное подспорье.
-
Обозначьте основные мысли текста, они называются тезисами. Их можно записывать как угодно - цитатами (в случае, если нужно передать авторскую мысль) либо своим собственным способом. Однако помните: изобиловать цитатами можно тогда, когда вы используете текстуальные конспекты. Кроме того, дословную выдержку из текста всегда заключайте в скобки и помечайте ссылкой на источник и автора.
При конспектировании лекций рекомендуется придерживаться следующих основных правил.
-
Не начинайте записывать материал с первых слов преподавателя, сначала выслушайте его мысль до конца и постарайтесь понять ее.
-
Приступайте к записи в тот момент, когда преподаватель, заканчивая изложение одной мысли, начинает ее комментировать.
-
В конспекте обязательно выделяются отдельные части. Необходимо разграничивать заголовки, подзаголовки, выводы, обособлять одну тему от другой. Выделение можно делать подчеркиванием, другим цветом (только не следует превращать текст в пестрые картинки). Рекомендуется делать отступы для обозначения абзацев и пунктов плана, пробельные строки для отделения одной мысли от другой, нумерацию. Если определения, формулы, правила, законы в тексте можно сделать более заметными, их заключают в рамку. Со временем у вас появится своя система выделений.
-
Создавайте ваши записи с использованием принятых условных обозначений. Конспектируя, обязательно употребляйте разнообразные знаки (их называют сигнальными). Это могут быть указатели и направляющие стрелки, восклицательные и вопросительные знаки, сочетания PS (послесловие) и NB (обратить внимание). Например, слово «следовательно» вы можете обозначить математической стрелкой =>. Когда вы выработаете свой собственный знаковый набор, создавать конспект, а после и изучать его будет проще и быстрее.
-
Не забывайте об аббревиатурах (сокращенных словах), знаках равенства и неравенства, больше и меньше.
-
Большую пользу для создания правильного конспекта дают сокращения. Однако будьте осмотрительны. Знатоки считают, что сокращение типа «д-ть» (думать) и подобные им использовать не следует, так как впоследствии большое количество времени уходит на расшифровку, а ведь чтение конспекта не должно прерываться посторонними действиями и размышлениями. Лучше всего разработать собственную систему сокращений и обозначать ими во всех записях одни и те же слова (и не что иное). Например, сокращение «г-ть» будет всегда и везде словом «говорить», а большая буква «Р» - словом «работа».
-
Бесспорно, организовать хороший конспект помогут иностранные слова. Наиболее применяемые среди них - английские. Например, сокращенное «ок» успешно обозначает слова «отлично», «замечательно», «хорошо».
-
Нужно избегать сложных и длинных рассуждений.
-
При конспектировании лучше пользоваться повествовательными предложениями, избегать самостоятельных вопросов. Вопросы уместны на полях конспекта.
-
Не старайтесь зафиксировать материал дословно, при этом часто теряется главная мысль, к тому же такую запись трудно вести. Отбрасывайте второстепенные слова, без которых главная мысль не теряется.
-
Если в лекции встречаются непонятные вам термины, оставьте место, после занятий уточните их значение у преподавателя.
Раздел 2. составление таблиц для систематизации учебного материала
Для систематизации и обобщения знаний учащихся предлагаю следующие методические приемы:
- составление таблиц формул, выражающих взаимосвязь физических величин, относящихся к какому - либо определенному разделу физики; - построение квалификационных схем, посредством которых выражаются отношения подчинения (между видовыми и родовыми понятиями, имеющими ближайший общий род);
- построение таблиц, в которых в определенной системе представлены свойства тел и основные наиболее важные их применения в технике;
- составление сводных таблиц, в которых учебный материал по теме и разделу отражен с помощью различных знаков и символов, в определенную систему на основе выбранного признака.
В дополнение к этим приемам мы можем добавить несколько методических приемов систематизации и обобщения знаний, который мы назовем блоком приемов логической структуризации учебного материала. Прежде всего это: - построение блок-схем, с помощью которых составляется логическая схема учебного материала в определенной последовательности; - построение графов-комплексов. Показ логико-гносеологической связи между явлениями, процессами, понятиями, величинами и указывает на последовательность их формирования; - составление структурно-логических конспектов. Раскрытие логической связи между элементами знаний. Структурно-логический конспект в процессе систематизации и обобщения знаний может иметь различное назначение в зависимости от дидактической цели ее применения. В начале изучения темы или раздела она способствует выделению в объекте существенных признаков, сосредоточению на них внимания учащихся и, таким образом, усвоению четких и ярких представлений и понятий. Этот процесс является своего рода систематизацией и обобщением, но он имеет локальный характер и относится к отдельным объектам; - построение логических конструкций, наглядно выражающих общую структуру расположения элементов раздела курса физики; - составление структурно-логической таблицы-комплекс.
Для формирования прочных математических приемов и
навыков решения используются различные формы. Одна из форм -
использование таблиц. Умение работать с таблицами необходимо не
только на уроках математики, но и на многих других предметах:
физика, химия и др. Умение работать с таблицами формирует более
устойчивые личностные качества: внимание, память, инициативность,
творческий потенциал.
Так, при изучении темы «Тригонометрические неравенства», для
освоения ее необходимо выучить 8 формул, предложенных учебным
пособием. Однако тему можно представить в табличном варианте и
необходимость в зазубривании трудных формул отпадет.
Мои наблюдения показали, что применение таблиц при обобщении и
систематизации знаний облегчает освоение материала.
В своей практике я часто использую таблицы при систематизации
знаний по пройденной теме. Используя такой прием регулярно, с
раннего времени обучения, я самостоятельно научилась
систематизировать знания с помощью таблиц и часто предлагаю их
использовать на уроках. После очередного составления таблицы по
теме «Тригонометрические уравнения и неравенства» я сделала вывод -
составление и применение таблиц при изучении математики
способствуют более качественному освоению материала.
Приведу пример таблицы, которую можно составить и использовать при
изучении данной темы.
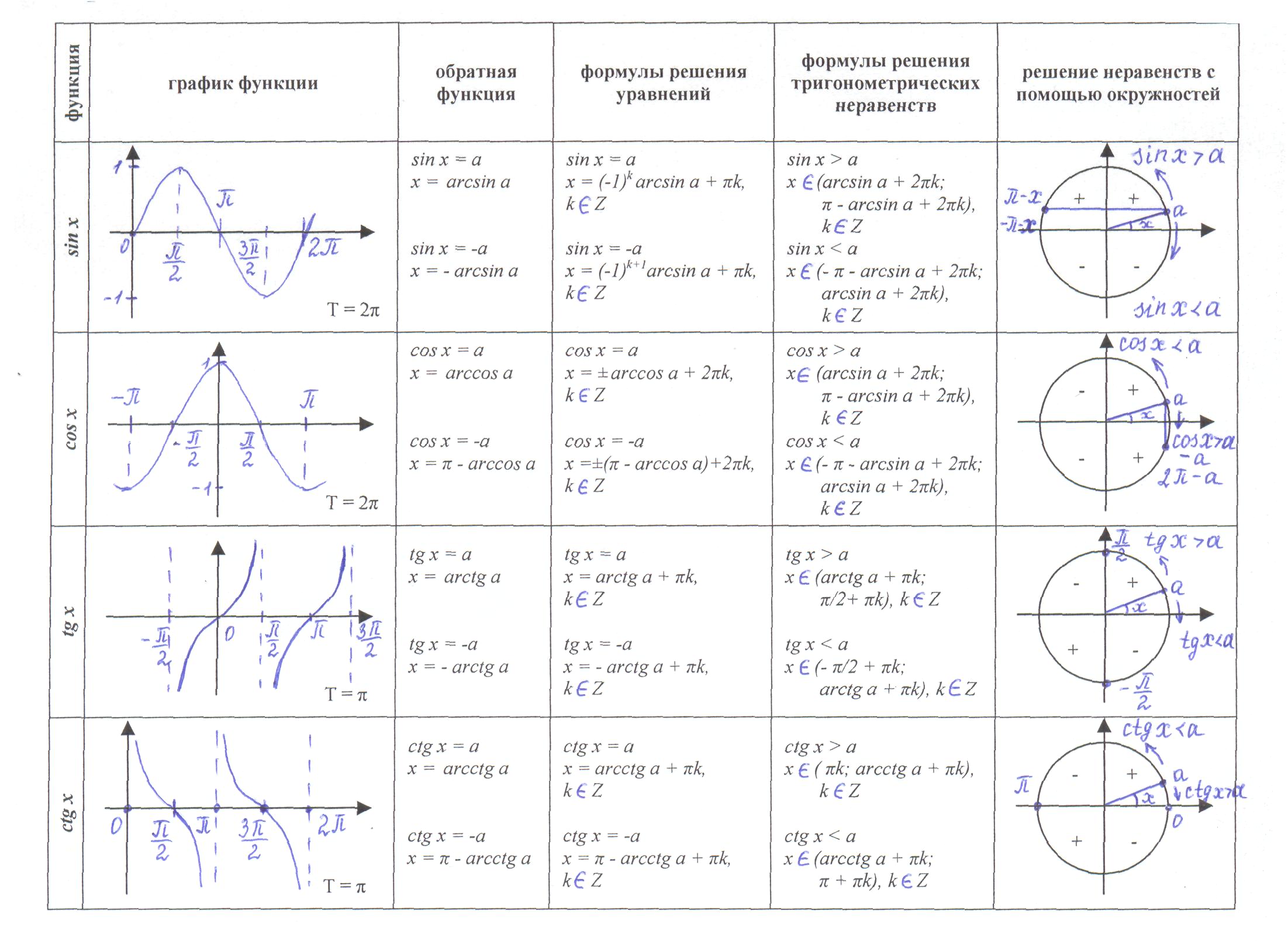
Представленная таблица позволяет сопоставить многие знания по
тригонометрическим функциям. Так, например, проведя анализ, можно
увидеть и объяснить решение тригонометрических уравнений без
использования формул, что особенно важно при подготовке к ЕНТ. Во
время этого периода свойственны определенные волнения, а часто и
стрессы, при которых информация может путаться или вообще «вылететь
из головы».
Математика - это предмет, насыщенный большим количеством формул. И
если есть возможность решения без использования нового материала, а
применения ранее полученного, то это обязательно нужно
использовать.
Самое главное - такая форма систематизации знаний способствует
осознанному запоминанию содержания материала, глубокому пониманию
полученных знаний.
Таблицы как систематизация знаний обеспечивает наличие принципов
научности, информативности. Сегодня большое внимание уделяется
развитию самостоятельности. И один из важных способов формирования
самостоятельности - это исследовательская работа. Раздел 3. работа
над материалом учебника
Успехи в изучении математики на уроках и при выполнении домашнего задания зависят, прежде всего, от умений и навыков учащихся работать с учебником. В начальных классах начинается формирование этих навыков и его сложность обусловлено еще и специфичностью учебников.
Перед каждым учителем возникает не менее важная проблема: обучение учащихся самостоятельно работать с учебником.
Система работы с учебником, раскрывающая концепцию авторов, обычно дается в соответствующих методических пособиях. Учителю при подготовке к урокам перед началом учебного года необходимо:
- внимательно изучить содержание программ и учебников;
- определить необходимую дополнительную литературу;
- определить основные направления работы по обучению учащихся умению работать с учебником и четко определить перечень основных формируемых при этом умений и навыков.
В начальных классах учитель, организуя работу с учебником, стремится сформировать у учащихся отношение к учебнику как руководству его учебной работой, помощнику при самостоятельной работе в классе и дома, воспитывает у них привычку искать ответы на свои вопросы, прежде всего, в учебнике, и лишь потом - у взрослых.
Начиная обучение в любом классе, учитель знакомить учащихся с принятыми в учебнике условными обозначениями и их назначением. Ученикам он объясняет расположение учебного материала, упражнений для повторения, назначение иллюстраций, справочного материала. Очень важно научить детей находить нужные темы по оглавлению или содержанию учебника, т.е. учит их работать с библиографическим аппаратом учебника. Все это относится также и к другим учебным пособиям (дидактические материалы, справочники и т.п.).
Всякая работа с учебником начинается с вступительной беседы учителя, где учитель мотивирует необходимость той или иной формы или приема работы, выделяет наиболее существенное, дает, дает рекомендации по использованию образцов записей, по запоминанию необходимых правил, способов решений.
В зависимости от этапа урока, работа с учебником может быть организована по-разному.
1. Работа с учебником при изучении нового материала
При изучении новой темы в первом классе, учащиеся работают по учебнику под руководством учителя. Приемы и формы работы определяются содержанием изучаемого материала. Например, при изучении вычитания 12-9 (в учебнике имеется рисунок наборного полотна), после вступительной беседы учитель без своего объяснения у доски просит учащихся воспроизвести на наборном полотне (демонстрационном, индивидуальном) то, что показано на рисунке и далее переходит к обоснованию выбранных действий и записи решения: 12-9=12-2-7=3. При изучении свойства сложения (4+3)+2, учитель, в зависимости от уровня подготовленности класса, может выбрать одну из последовательностей работы по учебнику:
1) беседа по рисунку учебника, воспроизведение действий на наборном полотне и запись примера;
2) работа на наборном полотне, запись примера и закрепление беседой по рисунку.
В процессе обучения умению работать с учебником, преподаватель может использовать, в частности, такие учебные работы:
- нахождение в учебнике ответа на поставленный вопрос и изложение его своими словами;
- самостоятельное выделение основных мыслей, фактов;
- составление плана изучения материала;
- самостоятельное сравнение, обобщение и классификация материала;
- самостоятельное объяснение имеющихся в учебнике образцов записи, рисунков и т.п.;
- установление связей между отдельными темами;
- приведение новых, своих примеров, относящихся к изучаемому материалу и т.д.
2. Работа с учебником при закреплении материала
При закреплении материала продолжаются те же формы работы с учебником, что и при его изучении. На данном этапе они еще более конкретизируются.
При решении задач учитель просит прочитать ее про себя, выделить условие и вопрос. Потом они вслух пересказывают содержание задачи своими словами (можно без числовых данных) представляя при этом реальную жизненную ситуацию. После этого учащиеся выделяют слова, которые можно использовать при краткой записи, выполняют ее (у доски, самостоятельно на местах). По завершении всей работы над задачей, еще раз в ходе фронтальной беседы повторяются все этапы работы, отвечая на вопросы типа: "Почему мы пересказывали задачу?", "Почему выделили главные слова?", и т.п. При таком подходе учащиеся учатся мотивировать свою деятельность.
При решении примеров учитель учит определять виды упражнений и их назначение. Важно также научить учащихся предварительно определить правила, необходимые для выполнения упражнения, находить аналогичные упражнения из ранее изученных материалов. После выполнения каждого упражнения ученик должен уметь подводить итог выполненной работы.
Предлагая учащимся домашнее задание, полезно с учащимися составлять план его выполнения по учебнику: что надо повторить, в какой последовательности выполнять, на что обратить внимание при решении задачи и т.п.
Результат деятельности в формировании навыков работы с учебником зависит от наличия навыков организации умственного труда у самого преподавателя.
Раздел 4. подготовка реферата
Реферат - представляет собой теоретическое изучение какого-либо понятия.
Размер реферата 20-30 листов.
Реферат (от латинского «referre» - докладывать, сообщать) - небольшая письменная работа, посвященная определенной теме, обзору источников по какому-то направлению. Обычно целью реферата является - сбор и систематизация знаний по конкретной теме или проблеме.
Тема реферата должна увлекать, в первую очередь, самого студента, ведь ему придётся изрядно потрудиться над её раскрытием.Темы рефератов, как правило, предлагают преподаватели. Студент выбирает интересную для него тему из общего списка и согласовывает свой выбор с преподавателем.
В ходе выполнения работы студент не только получает сведения в определенной области, но и развивает практические навыки анализа научной литературы.
Ниже перечислены основные требования к оформлению работы, но следует помнить, что на некоторых кафедрах университета разработаны собственные правила оформления реферата.
Оформляем и структурируем
Реферат состоит из введения, основного текста, заключения и списка литературы. Реферат при необходимости может содержать приложение. Каждая из частей начинается с новой страницы.
Заголовки должны четко и кратко отражать содержание разделов, подразделов. Заголовки следует печатать с прописной буквы. Переносы слов в заголовках не допускаются. Если заголовок состоит из двух предложений, их разделяют точкой. В конце заголовка точку не ставят. Расстояние между заголовком и последующим текстом должно быть не менее 10 мм.
Титульный лист
Титульный лист является первой страницей реферата, заполняется по строго определенным правилам и оформляется на отдельном листе бумаги (скачать образец).
Нормы оформления титульного листа могут зависеть от принятых на кафедре стандартов. Поэтому рекомендуется познакомиться с работами предшественников-студентов старших курсов. Тем не менее существует общепринятый стандарт оформления титульного листа реферата.
Оглавление
Оглавление размещается после титульного листа. Слово «Оглавление» записывается в виде заголовка (по центру). В оглавлении приводятся все заголовки работы и указываются страницы. Оглавление должно точно повторять все заголовки в тексте.
Во введении реферата указываются актуальность темы реферата, цель реферата, задачи, которые необходимо решить, чтобы достигнуть указанной цели. Кроме того, во введении реферата дается краткая характеристика структуры работы и использованных информационных источников (литературы). Объем введения для реферата - 1-1,5 страницы.
Основной текст
Основной текст разделён на главы. Если текст достаточно объёмный, то главы дополнительно делятся на параграфы. Главы можно заканчивать выводами, хотя для реферата это не является обязательным требованием. Главы и параграфы реферата нумеруются. Точка после номера не ставится. Номер параграфа реферата включает номер соответствующей главы, отделяемый от собственного номера точкой, например: «1.3». Заголовки не должны иметь переносов и подчеркиваний, но допускается выделять их полужирным шрифтом или курсивом.
Если реферат маленький (общий объем - 8-10 стр.), то его можно не разбивать на главы, а просто указывается «Основная часть», которая выступает в качестве заголовка единственной главы. Однако все-таки предпочтительнее, чтобы текст был разбит на главы (хотя бы две). Обычно в реферате 3-4 главы. Каждая новая глава начинается с новой страницы. На основную часть реферата приходится 6-16 страниц.
Заключение
В заключении формируются выводы, а также предлагаются пути дальнейшего изучения темы. Здесь необходимо указать, почему важны и актуальны рассматриваемые в реферате вопросы. В заключении должны быть представлены ответы на поставленные во введении задачи, сформулирован общий вывод и дано заключение о достижении цели реферата. Заключение должно быть кратким, четким, выводы должны вытекать из содержания основной части.
Список литературы
При составлении списка литературы следует придерживаться общепринятых стандартов. Список литературы у реферата - 4-12 позиций. Работы, указанные в списке литературы, должны быть относительно новыми, выпущенными за последние 5-10 лет. Более старые источники можно использовать лишь при условии их уникальности. Как оформить список литературы, можно узнать здесь.
Приложения
Приложения должны нумероваться арабскими цифрами. В правом верхнем углу указывают: «Приложение 1», а с новой строки - название приложения
ПРАВИЛА НАПИСАНИЯ И ОФОРМЛЕНИЯ РЕФЕРАТА
Текст работы представляется на стандартных листах писчей бумаги для машинописи или ксерокопирования формата А4 (210 х 297 мм). Работа печатается на одной стороне листа на принтере. Стандартные поля: 3 см - с левой стороны, 1,5 см - с правой стороны, 2 см - нижний и верхний поля. Шрифт Times New Roman (14 пт), междустрочный интервал полуторный, текст выравнивается по ширине, абзацный отступ 10 мм. Нумерация страниц - сверху по центру. Примерный план написания реферата:
В начале реферата должное быть оглавление, в котором указываются номера страниц по отдельным главам. Каждая глава текста должна начинаться с нового листа, независимо от того, где окончилась предыдущая. Заголовки разделов прописными буквами ВВЕДЕНИЕ, ЗАКЛЮЧЕНИЕ без точек в конце. Титульный лист не нумеруется.
Ведение. Во введении необходимо обосновать выбор данной темы, коротко рассказать о том, почему именно она заинтересовала автора.
I глава. Вступительная часть. Это короткая глава должна содержать несколько вступительных абзацев, непосредственно вводящих в тему реферата.
II глава. Основная научная часть реферата. Здесь в логической последовательности излагается материал по теме реферата. Эту главу целесообразно разбить на подпункты - 2.1.,2.2. (с указанием в оглавлении соответствующих страниц).
Заключение. В той главе автор подводит итог работы, делает краткий анализ и формулирует выводы.
В конце работы прилагается список используемой литературы. Литературные источники следует располагать в следующем порядке:
- энциклопедии, справочники;
- книги по теме реферата (фамилии и инициалы автора, название книги без кавычек, место издания, название издательства, год издания, номер (номера) страницы);
- газетно-журнальные статьи (название статьи, название журнала, год издания, номер издания, номер страницы).
Фотографии, рисунки, карты, схемы можно оформить в виде приложения к работе.
Теоретическая глава чаще всего пишется по принципу: от общего к частному. То есть вначале рассматриваются общие подходы к чему-либо, затем они конкретизируются.
Когда описывается какое-либо явление, то оно может рассматриваться:
1) по хронологическому принципу
То есть рассматривается явление во временном интервале, или в историческом аспекте.
2) по логическому принципу
В этом случае рассмотрение явления нужно делать по следующему плану:
-феноменология (т.е. описание проявлений данного явления)
-место данного явления среди других, его взаимосвязи, его компоненты, связи между компонентами
-определения данного явления, общее и отличное в определениях разных авторов
-практика, использование данного явления
В процессе описания какого-либо явления, студенту также необходимо указывать свою точку зрения.
Например, студент может из 100 определений, найденных им выбрать в качестве наиболее подходящего для данной работы какое-то одно. При этом нужно указать, почему именно оно выбрано.
Для того, чтобы грамотно написать теоретическую главу, необходимо проработать достаточно большое количество научных, научно-методических и других источников по теме диплома. Как правило - не меньше 30.
В процессе проработки теоретических источников нужно выделять и отмечать тот текст, который значим для данного параграфа, главы диплома. Эти фрагменты текста можно помещать в дипломное исследование как цитату, как иллюстрацию к вашему анализу, сопоставлению.
В теоретической части нельзя целиком помещать разделы и главы из учебников, книг, статей.
В конце каждого параграфа теоретической главы должны быть сделаны небольшие тезисные выводы. После теоретической главы следует раздел: Выводы по теоретической главе, в котором освещаются основные теоретические положения, рассмотренные в данной главе.
Требования к выполнению реферата
Реферат является научной работой, поскольку содержит в себе элементы научного исследования. В связи с этим к реферату должны предъявляться требования по оформлению, как к научной работе.
Правила оформления научных работ являются общими для всех отраслей знаний и регламентируются государственными стандартами, в частности ГОСТом 7.1 - 84. "Библиографическое описание документа: Общие требования и правила составления", "Правилами составления библиографического описания". Для рефератов необходимо выполнять следующие требования: общие требования, правила цитирования, правильное оформление ссылок, библиографического списка, правила сокращения и использования числительных. Очень полезно запомнить данные правила сразу, чтобы впоследствии не уделять этому много времени.
При оформлении текста реферата следует учитывать, что открывается работа титульным листом, где указывается полное название ведомства, университета, факультета, кафедра, тема реферата, фамилии автора и руководителя, место и год написания. На следующей странице, которая нумеруется сверху номером 2, помещается оглавление с точным названием каждой главы и указанием начальных страниц.
Общий объем реферата не должен превышать 15-20 страниц для печатного варианта. При печатании текста реферата абзац должен равняться четырем знакам (1,25 см.).
Поля страницы: левое - 3 см., правое - 1,5 см., нижнее 2 см., верхнее - 2 см. до номера страницы. Текст печатается через 1,5 - 2 интервала. Если текст реферата набирается в текстовом редакторе Microsoft Word, рекомендуется использовать шрифты: Times New Roman Cyr или Arial Cyr, размер шрифта - 14 пт. При работе с другими текстовыми редакторами шрифт выбирается самостоятельно, исходя из требований - 60 строк на лист (через 2 интервала).
Каждая структурная часть реферата (введение, главная часть, заключение и т.д.) начинается с новой страницы. Расстояние между главой и следующей за ней текстом, а также между главой и параграфом составляет 2 интервала.
После заголовка, располагаемого посредине строки, не ставится точка. Не допускается подчеркивание заголовка и переносы в словах заголовка. Страницы реферата нумеруются в нарастающем порядке. Номера страниц ставятся вверху в середине листа.
Титульный лист реферата включается в общую нумерацию, но номер страницы на нем не проставляется (это не относится к содержанию реферата).
Раздел 5. решение задач и упражнений по образцу.
Психологические особенности решения задач.
Согласно современным и психологическим структура математического мышления представляет собой пять пересекающихся подструктур. В зависимости от индивидуальных особенностей человека любая из подструктур может занимать место преобладающей. В связи с этим одна и та же задача может решаться по-разному, в зависимости от индивидуальных особенностей решающего. Рассмотрим эти подструктуры.
Первая подструктура - Топологическая. Она помогает оперировать такими характеристиками, непрерывно - разрывно, связно- несвязно ,принадлежит не принадлежит, внутри - вые, порознь - вместе. Решающий ,у которого преобладает эта подструктура мышления, не любит торопиться. Каждое действие он делает очень подробно ,не пропуская ни одного звена. Это тонкий аналитик, он все проверит , не пропустит ошибок, отсюда и медлительность.
Вторая подструктура - Проективная.
Тот, у кого преобладает проективная подструктура предпочитает изучить любой математический объект с различных точек зрения, искать и находить различные применения предмета в практике. Решающий любит планировать, он не сделает первого шага, если не видит следующего. Он поражает нас широтой своего математического мышления, способностью отыскивать и предлагать совершенно неожиданные подходы и аспекты решения.
Третья подструктура - Порядковая.
Тот, у кого преобладает эта подструктура предпочитают сравнивать и оценивать в общем качественном виде: равно - не равно , больше - меньше, ближе - дальше , выше - ниже , и т. д. Ему важна форма объекта ,их соотношение , форма движения.
Четвертая подгруппа - Метрическая.
Акцентируется внимание на количественные характеристики. Они заворожены числом. Главный вопрос: Сколько? Он всегда выясняет, какова длина отрезка и т.д. Ему трудно понять, что ответ может не иметь числового значения. Он не любит решать задачи в общем виде. Решать задачи в общем виде не в его правилах. Он предпочитает решение по действиям, результатом каждого, из которых, является число.
Пятая подгруппа - Алгебраическая.
Стремится по возможности комбинациям. Он - торопыга. Не хочет подробно записывать, объяснять все шаги решения или обосновать собственные действия. Он «великий комбинатор», думает и делает быстро, фонтанирует идеи, предположения и гипотезы решения, но при этом часто ошибается. Доминантная подструктура математического мышления проявляет себя во всех математических действиях; и в зависимости от нее каждый выбирает свой индивидуальный метод решения. Как утверждал знаменитый И. В. Гете:
«Каждый слышит только то, что он понимает.»
Каждую задачу человек должен решить своим индивидуальным способом и лишь после этого пытаться понять иные методы рассуждений. Решение задач есть, неотъемлемая часть человеческой деятельности связана с решением каких-либо задач или проблем. Некоторые достигают своей цели и решают стоящие перед ними задачи с большим успехом, некоторые - с меньшим. Эта разница в успехе подмечается, обсуждается, комментируется, квинтэссенция таких замечаний как бы сохраняется в некоторых пословицах. Во всяком случае, имеется много поговорок, характеризующих с поразительной точностью типичные пути решения задач, остроумные, основанные на здравом смысле приемы, обычные уловки и обычные ошибки. В пословицах много проницательных и даже тонких высказываний, но разумеется, они не составляют стройной и научной системы. Тупо было бы считать пословицы авторитетным источником мудрости, применимым ко всем случаям жизни, но, с другой стороны, жалко пренебрегать такой наглядной иллюстраций эвристических приемов решения задач, какую нам дают пословицы. Здесь мы можем уделить место пословицам, разделяя их на группы, по которым следует вести решение.
1 этап.
При решении задач необходимо в первую очередь понять ее. И на это есть пословица: кто плохо понимает, плохо отвечает. Мы должны уяснить цель, которую должны достичь: обдумай цель, раньше, чем начать. Если мы не уяснили себе конечной цели, не трудно при решении сбиться с пути: с началом считается глупец, о конце думает мудрец. Недостаточно лишь понять задачу, необходимо желание решить ее: мудрый начинает с конца, глупый кончает в начале. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно: где есть желание, найдется путь.
2 этап.
Главное в решении задачи - составить план, наметить правильный ход решения: усердие - мать удачи; настойчивость убивает дичь; дуб не валиться с одного удара. Недостаточно, однако, многократно повторять попытки, следует испробовать различные средства, варьировать попытки: попробуй все ключи в связке; стрелы изготавливают из разных сортов дерева. Надо приноровить свои попытки к обстоятельствам: устанавливай свои паруса по ветру; раскраивай пальто по сукну. Если мы терпим неудачу, приходится пробовать другие средства: мудрый меняет свои решения, дурак никогда; ну, а если не терять из виду цели, будешь меньше блуждать в потемках; смысл рыбной ловли не в том, чтобы забрасывать удочку, а в том чтобы поймать рыбу. У знатока, возможно, не больше мыслей, чем у неопытного человека, но он лучше взвешивает достоинства своих мыслей и умеет лучше использовать их: мудрый создает орудие из всего, что попадается ему под руку.
3 этап.
Следует приступать к осуществлению своего плана своевременно: проверь, прежде чем прыгать; испытай, потом доверяй. Но, с другой стороны, не следует слишком долго колебаться: хочешь плавать без опасностей, не отправляйся в море. А вот наиболее частая погрешность вашего суждения: желаемое мы охотно принимаем за действительное. Нам план обычно дает лишь общий контур решения. Надо убедится, что детали соответствуют контуру; поэтому мы должны внимательно рассмотреть каждую деталь, одну за другой: ступень за ступенью лестница преодолевается; маленькие удары валят большие дубы.
4 этап.
Очень важным и поучительным этапом является возвращение к уже решенной задаче: тот, кто не думает снова, не сможет думать правильно. При вторичном изучении можно найти дополнительные подтверждения правильности полученного результата, потому что два доказательства лучше одного: с двумя якорями безопасно плыть.
5 этап.
Так же есть «синтетические» пословицы, выделяющие более тонкие отношения: цель подскажет путь. Если вам нужен совет обратитесь к Что, обратитесь к Почему: ничему не верьте, но сомневайтесь только в том, что вызывает сомнение; найдя первый гриб или сделав первое открытие, осмотритесь вокруг - они родятся кучками.
Раздел 6. решение вариативных задач и упражнений
Схемы решения задач.
1. Все задачи подразделяются на разделы: по характеру объектов, по отношению к теории, по характеру требований.
2. Под процессом решения задач необходимо понимать процесс, начинающийся с момента получения задачи до момента полного ее завершения. Этот процесс состоит не только из изложения уже найденного решения, а из ряда этапов.
3. Кроме стандартных задач, при решении которых используются общие правила и положения, существуют нестандартные задачи. Нестандартные задачи - это задачи, для которых не имеется общих правил и положений, определяющих точную программу их решения. Для решения этих задач составляются свои схемы. Для того, чтобы легко решать стандартные задачи (они являются основными, т.к. решение нестандартных задач сводятся к решению стандартных), нужно: Помнить (держать в памяти) все изученные общие правила, формулы, тождества и общие положения, определения и теоремы. Уметь развертывать правила, формулы, а также определения и теоремы
- последовательности шагов решения задач, соответствующих видов. Значение наглядности и применение на уроках математики.
Применение различных средств наглядности активизирует учащихся, возбуждает их внимание и тем самым помогает их развитию, способствует более прочному усвоению материала, дает возможность экономить время. Тот факт, что математике присуща большая абстрактность, определяет и характер средств наглядности, и особенности применения их. В таких учебных предметах, как естествознание, история, география, наглядные пособия чаще всего используются для показа изучаемых объектов. Чтобы учащиеся могли составить наиболее правильное, наиболее полное представление о животном или растении, о том или ином событии, о природном явлении и т.п., все это необходимо показать в возможно более естественном виде и так, чтобы хорошо были различимы все нужные детали.
Чтобы исследовать количественные отношения и формы в чистом виде, необходимо совершенно отделить их от содержания. В этом и оказывают помощь учителю различные средства наглядности и в первую очередь модели, чертежи, схемы, которые более всего отвечают указанному требованию.
Раздел 7. выполнение моделей для демонстрации теорем.
В обучении математике используются различные виды наглядных пособий:
-
Предметы окружающей среды. С первых же дней пребывания детей в школе при обучении их счету и действиям сложения и вычитания, предметы окружающей обстановки могут быть использованы в качестве счетного материала. Таким материалом могут служить книги, тетради, карандаши, счетные палочки и т. д. Отдельные предметы могут быть использованы и в дальнейшем: при ознакомлении учащихся с элементами геометрии. На них можно показывать различные пространственные формы.
-
Демонстрационные изобразительные пособия. К этому виду наглядных пособий относятся, прежде всего, картины и учебные таблицы с изображением ряда знакомых детям предметов, наборы картинок, картины со вставками, аппликации. Используются как счетный материал, что значительно расширяет возможности учителя при обучении детей счету, или для иллюстрирования задач. К демонстрационным изобразительным пособиям относятся также модели измерительных приборов и инструментов (часовой циферблат, весы), модели мер ( метра, литра), муляжи и макеты хорошо известных детям товаров. Модели используются при изучении мер и обучении измерениям. А муляжи и макеты - как иллюстративный материал при составлении задач. Наконец, к демонстрационным изобразительным пособиям относятся изображения и модели различных геометрических фигур.
-
Таблицы. Таблицами называют текстовые или числовые записи, располагаемые в определенном порядке. Чаще всего в виде колонок, а также сгруппированные вместе серии рисунков и схем с текстом или без него. Таблицы издаются на больших листах бумаги, наклеенных для удобства пользования на ткань или картон. По своему значению таблицы могут быть разделены на группы:
-познавательные;
- инструктивные;
- тренировочные;
- справочные;
Разумеется, это деление в какой - то мере условно.
К познавательным таблицам относятся такие, которые содержат в себе новые сведения и поэтому чаще всего используются при объяснении нового материала. К их помощи можно прибегать также при повторении с целью расширения и обобщения знаний учащихся. Примером познавательных таблиц может служить нумерационная таблица, показывающая разряды и классы счетных единиц, изготавливаемая в соединении с наборным полотном. В таком виде она используется и как тренировочная. Познавательным таблицам относится также серия таблиц " Измерение длины", " Измерение веса", " Измерение площади", которые дают наглядное представление об основных мерах и содержат единичные отношения их, и ряд других.
Инструктивные таблицы в наглядной форме дают указания по выполнению тех или иных действий, связанных с формированием навыков написания цифр, решения задач, вычислительных навыков. К этим таблицам относятся таблицы с образцами рукописных цифр, с примерами, указывающими порядок выполнения арифметических действий, с примерами алгоритмов действий и др. такие таблицы вывешиваются в классе на более или менее продолжительное время, чтобы они помогали учащимся в их работе, давали необходимые указания.
Тренировочные таблицы предназначаются для проведения многократных упражнений, с целью формирования вычислительных навыков. Наиболее известными из таких таблиц являются таблицы для устных вычислений. Эти таблицы освобождают учителя от необходимости выписывать длинные ряды чисел и тем самым облегчают его работу и позволяют экономить время.
Справочные таблицы содержат материал, который часто бывает нужен учащимся как при решении примеров и задач, так при выполнении практических работ. Они, как и инструктивные таблицы, вывешиваются в классе на продолжительное время.
-
Счетные приборы. К этому виду наглядных пособий относятся счеты, абаки, арифметический ящик. Счеты применяются, начиная с первого класса, в течение ряда лет при обучении счету, при изучении нумерации и арифметических действий. На демонстрационных или классных счетах на первых порах целесообразно иметь сначала только одну проволоку с десятью косточками. Потом две с двадцатью. Остальные должны быть в это время закрыты листом бумаги или сняты совсем.
Абак или счетная доска, является обычно самодельным пособием. Арифметический ящик изготавливается в виде ящика кубической формы с двумя открывающимися стенками. Содержит оно большое количество счетного материала: деревянные кубики, бруски, равные десяти кубикам, выложенным в ряд. Кубики, бруски и доски используются при обучении счету и изучении нумерации. При этом наглядно могут быть показаны соотношения между основными и разрядными единицами и десятичный состав чисел.
-
Измерительные инструменты. Измерительные инструменты в учебном процессе играют двоякую роль. Во- первых, они могут быть использованы по прямому назначению для измерений при выполнении различных работ или для получения данных к задачам практического содержания. Во- вторых, они могут служить в качестве вспомогательных средств, при изучении мер и единичных отношений между мерами. В начальных классах применяются инструменты для измерений длины, веса, емкости, площади и для построения и выполнения основных измерительных работ. К этим инструментам относятся: - линейка чертежная, угольники, линейка метровая, рулетка, циркуль; - весы чашечные с разновесами, весы циферблатные; - кружки литровая, пол- литровая; - циферблат; - палетка; - классный циркуль;
-
Иллюстрации. Под иллюстрациями обычно понимают помещенные в учебнике рисунке и схематические изображения различных предметов и групп предметов. А также планы, чертежи, схемы, таблицы, как и рассмотренные выше наглядные демонстрационные пособия, иллюстрации используются в самых различных случаях. С их помощью наглядно показываются предметы, о которых идет речь, выполняемые действия или разъясняется содержание задачи.
При необходимости иллюстрации к отдельным задачам могут быть сделаны на больших листах бумаги или в виде диапозитивов. В настоящее для каждого класса издаются серии карточек с математическими заданиями, включающие иллюстрации. Эти карточки предназначаются для обучения составлению и решению задач.
-
Дидактический материал. Для формирования математических понятий, а также для выработки вычислительных, измерительных и графических навыков в начальных классах необходимо использовать разнообразный дидактический материал. Дидактическим материалом по математике называют учебные пособия для самостоятельной работы учащихся, позволяющие индивидуализировать и активизировать процесс обучения. Дидактический материал по математике можно подразделить на:
а) предметный дидактический материал;
б) дидактический материал в виде карточек с математическими заданиями.
К предметному дидактическому материалу относятся: счетные палочки, наборы разнообразных геометрических фигур, модели монет и т. п. Предметный материал необходимо использовать как при объяснении новых знаний, так и при их закреплении.
Дидактический материал в виде карточек с математическими заданиями обеспечивает приспособление к индивидуальным особенностям учащихся. Некоторые виды карточек позволяют освободить учащихся от переписывания заданий, что дает возможность выполнить больше упражнений.
Раздел 8. Подготовка доклада
В первую очередь, советуем по возможности выбирать ту тему, которая наиболее вас заинтересовала. Если вашему классу дали список тем доклада, то советуем из него выбрать ту, которая вам понравилась. Ведь известно, что всегда будет работаться намного быстрее и легче, если человек будет просто «жить» своей работой. Однако если такой возможности нет, то из установленной учителем темы для вас, постарайтесь найти наиболее интересные факты, которые смогли бы заинтересовать вас и ваших одноклассников. По возможности, советуем включать только проверенный материал, который вы сможете найти в научной литературе, также можно использовать новые сведения о вашей теме, которую легче всего будет найти в интернете.
Постарайтесь спланировать свои действия.
Несмотря на то, что доклад не считается довольно объемной работой, однако, для нее также потребуется план, где будут указаны основные моменты. Заметим, что очень часто учителями биологии требуется от учеников написать доклад о животных. Такая тема является всегда интересной для ученика, а подобная тематика распространена не только в интернете, но и в энциклопедиях. Тем не менее, более сложным будет задание: написать доклад по английскому языку. Здесь надо, в первую очередь, придумать порядок выкладки материала на родном языке. Далее набросайте основные моменты, которые вы бы хотели изложить. И только после этого беритесь излагать свои мысли на английском языке.
Приведем пример вашего плана для доклада:
-
Выбор источника информации.
-
Сбор необходимой информации.
-
Основные моменты из собранного материала.
-
Свод частей доклада в единый текст.
-
Выводы по теме вашего доклада.
Не смотря на то, что данные пункты являются очень простыми и их достаточно всего лишь держать у себя в голове, все же желательно написать их на бумаге и в точности их придержаться.
Комбинируйте все источники своей информации
В данном случае мы советуем комбинировать источники с интернета с работами из них. Таким образом, вы не только бессмысленно скопируете информацию с интернета, но и сможете прочитать ее, тем самым, подготовившись к выступлению. Такое стремление к выполненной работе будет обязательно оценено вашими преподавателями. Одновременно напрашивается вывод, что, чем больше источников вы сможете задействовать при написании вашего доклада, тем качественнее будет ваша работа.
Речь защиты доклада
Не маловажной принято считать и речь доклада, поскольку именно она будет отображать вашу подготовку. Чем качественнее будет подготовка к докладу, тем лучше будет ваша защита. Не обязательно заучивать наизусть предложения из доклада. Можно, к примеру, опираться на подготовленные тезисы, которые вы внесли в свой доклад и т.д. Выделите наиболее важную информацию в докладе и просто несколько раз прочитайте её. Если информация, которую вы подготовили действительно интересная, то вы обязательно ее запомните и донесете своему учителю и одноклассникам.
Раздел 9 Правила выполнения чертежей
Выносной элемент ограничивается тонкой волнистой линией, может содержать подробности, не указанные на соответствующем изображении, и располагается по возможности ближе к нему.
Геометрические построения
1. Не проще ли будет построить сложный чертеж, если разложить решение любой графической задачи на ряд отдельных простейших операций?
2. Возможно ли выполнение сложных чертежей на ЭВМ без знания сущности тех или иных простейших графических построений?
3. Поможет ли Вам овладение приемами простейших геометрических построений в развитии вашего будущего инженерного творчества?
Для того, чтобы построить чертеж детали, провести плоскостную разметку для изготовления или обработки детали, необходимо выполнить ряд геометрических построений.
Геометрическими построениями называют графические способы решения любой практической задачи, при которых все действия производятся чертежными или разметочными инструментами.
2.1 Проведение перпендикуляра
2.1.1 Построение перпендикуляра к прямой из точки, лежащей вне прямой Нанесение размеров ГОСТ 2.307-68 (в ред. 2004 г.) устанавливает правила нанесения размеров и предельных отклонений на чертежах и других технических документах на изделия всех отраслей промышленности и строительства. Правила и рекомендации при простановке размеров
Порядок построения следующий (рис.2.1):
1. Из заданной точки С, как из центра, провести дугу окружности произвольного радиуса R, пересекающую прямую а в точках 1 и 2.
2. Из точек 1 и 2 провести дуги окружностей произвольного радиуса R1 до взаимного пересечения в точке D.
3. Через точки С и D провести прямую линию.
Линия CD перпендикулярна к заданной прямой а.
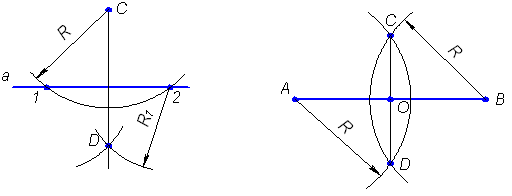
Построение перпендикуляра к середине отрезка
Порядок построения следующий:
1. Из концов отрезка АВ проводят дуги радиусом R, величиной большей, чем половина отрезка.
2. Точки пересечения дуг соединяют прямой линией СD.
Линия CD является перпендикуляром к отрезку АВ, точка О - середина отрезка.
Изложение предпочтительно вести в настоящем времени. Не следует смешивать в одной фразе настоящее время с прошедшим или будущим. Следует использовать повествовательную форму изложения, избегая, по возможности, возвратной формы глаголов (не вычисляется по формуле, а вычисляют по формуле). Автор должен писать о себе в третьем лице, не употребляя местоимений "я" и "мы" (не по - моему мнению, а по мнению автора). В документе должны применяться научно-технические термины и обозначения, установленные соответствующими стандартами, а при их отсутствии - общепринятые в научно-технической литературе. Если в документе использовано более пяти обозначений или сокращений необходимо ввести раздел "Обозначения и сокращения" или "Обозначения", "Сокращения". Текст раздела следует располагать перед текстом основных разделов. Перечень принятых обозначений и сокращений составляют в алфавитном порядке или в порядке их первого упоминания в тексте документа, при этом приводят их расшифровку или необходимые пояснения.
Определение центра дуги окружности
Построение сопряжения дуги и прямой линии Построение сопряжения двух дуг
Пример. Заданные окружности находятся внутри сопрягающей дуги (внутреннее сопряжение)
Построение внешней касательной к двум окружностям Построение овала по двум осям
Выполнение чертежей деталей, имеющих сопряжения
Уклон - это тангенс угла наклона одной прямой к другой
Конусность - это отношение разности диаметров двух поперечных сечений усеченного конуса к длине между ними
Правила нанесения размеров на чертежах и других технических документах на изделия всех отраслей промышленности и строительства установлены ГОСТ 2.307 - 68. - это очень важная часть чертежа. Пропуск или ошибка хотя бы в одном из размеров делают чертеж непригодным к использованию. Последовательность нанесения размеров
Разрез - изображение предмета, мысленно рассечённого одной или несколькими плоскостями. На разрезе показывают то, что получается в секущей плоскости и что расположено за ней. Плоскую фигуру, находящуюся в секущей плоскости (сечение), заштриховывают
Раздел 10. Правила оформления исследовательской работы
Исследовательская работа - это письменный отчёт о каком- либо явлении или процессе. В ходе исследовательской работы составитель должен ответить на вопросы: зачем (исследовательская проблема), что (область исследования), и как (метод исследования) исследовали и каковы результаты и выводы, которых достигли в ходе работы.
Тема исследовательской работы может охватывать
любую предметную сферу.
В исследовательской работе нельзя представлять мнения других
авторов, не делая ссылок. В исследовательской работе можно
использовать выводы других авторов, но, сравнивая и анализируя эти
выводы, необходимо сделать собственные.
Общие требования
Исследовательская работа выполняется на формате А4 в мягком переплёте. Работа должна быть выполнена на компьютере. Работа пишется только на одной стороне страницы. Размер шрифта 12 (14) Times NewRoman, обычный, интервал между строк 1(1,5).. Все страницы нумеруются, начиная с титульного листа. Цифру номера страницы ставят внизу по центру страницы, на титульном листе номер страницы не ставят. Каждый новый раздел (введение, главы, параграфы, заключение, список источников, приложения) начинаются с новой страницы. Заголовок располагается посередине строки, точку в конце заголовка не ставят.
Логическое построение работы:
· Титульный лист
· Оглавление
· Введение
· Основная часть работы
- теоретическая часть
- практическая часть
· Заключение
· Использованная литература
· Приложения
1.Титульный лист
· Название образовательного учреждения, при котором выполнена работа, регион и населённый пункт
· Название детского объединения
· Тема работы
· Фамилия, имя, отчество автора
· Возраст (класс)
· Фамилия, имя, отчество руководителя работы
· Год выполнения работы
2.Содержание (оглавление)
Оглавление помещается после титульного листа, в котором приводятся все заголовки работы и указываются страницы, с которых они начинаются. Заголовки оглавления должны точно повторять заголовки в тексте.
Примечание: содержание должно быть вынесено на отдельную страницу, как и любой другой структурный элемент.
3.Введение
· обоснование актуальности темы,
· постановка проблемы,
· определяются объект, предмет и цель исследования,
Примечание: цель работы должна быть сформулирована конкретно, а не в общих словах
· формируется гипотеза, задачи и методологические основы исследования
· описывается новизна и практическая значимость работы
Примечание: корректировка введения может продолжаться до полного завершения всей работы. Объем введения - не более одной страницы машинописного текста. Никаких иллюстраций в раздел «Введение» помещать не нужно.
4.Основная часть работы.
· Теоретическая часть
- обзор литературы по теме исследования;
- анализируется и обобщается собранный материал
Анализируя литературу можно воспользоваться следующей схемой:
- автор, краткая справка о нем;
- проблема, которую автор ставит в своём исследовании;
- источники, на основании которых написано исследование;
- основные идеи, концепции, выдвинутые автором;
- выводы автора;
- ваше мнение о данном исследовании.
Примечание: необходимо, чтобы в процессе изложения содержания этой части работы автор осуществил переход от анализа единичных факторов к их теоретическому обобщению. В конце теоретической части обязательны выводы, содержащие основные теоретические положения. Цитируемые в рукописи места должны иметь точные указания, ссылки на источник.
Ссылки
Если в работе содержатся цитаты или ссылки на высказывания, необходимо указать номер источника по списку и страницу в квадратных скобках в конце цитаты или ссылки. Например: По мнению Эйнштейна, пространство и время относительны, они зависят от скорости движения системы отчёта.
· Практическая часть
- содержит конкретные разработки содержания и методов, показывающих пути решения поставленных проблем и задач;
- описывается то, что и как делал автор для доказательства выдвинутой гипотезы, представляет собой методику исследования
- описываются результаты, полученные в ходе исследования
Примечание: данные экспериментальной части исследования должны быть представлены в виде графиков, таблиц, диаграмм и т.п. В конце главы необходимо четко сформулировать выводы по практической части работы.
5.Заключение
· подведение итогов проведенного исследования,
· доказана теоретическая новизна и практическая значимость исследования,
· определены возможные перспективы дальнейшей разработки проблемы;
· рекомендации
· Общие выводы по работе в целом
Примечание: выводы не должны быть кратким изложением работы или ее раздела. Первым надо располагать самый важный вывод, а далее располагать их в порядке убывания важности.
· выявлено соответствие выводов поставленным целям и задачам
· определены возможные перспективы дальнейшей разработки проблемы.
Примечание: заключение не должно повторять содержание глав, а представлять обобщение более высокого уровня, синтез всех полученных данных.
6.Список использованной литературы
· список литературы должен содержать разнообразные виды изданий: нормативные, справочные, научные, периодические и т.д.
· Список литературы содержит перечисление всех упоминавшихся в тексте статей и книг. Он нужен для того, чтобы любой читатель мог найти любую книгу или статью по приведенным в списке данным.
· Список составляется по определенному стандарту, который можно найти в любой научной статье.
· Статьи и книги в списке располагаются обычно в алфавитном порядке по фамилиям авторов. Если авторов несколько, место определяется фамилией первого из них. Обычно применяется такой порядок записи: фамилия, инициалы, название книги, место издания (город), название издательства, год. Если речь идет о статье, порядок следующий: фамилия, инициалы; название статьи; журнал, том, номер, год, страницы.
· Если в списке есть работы на иностранных языках, они следуют за списком русской литературы в порядке латинского алфавита.
7.Приложения
Размещение количественных данных делается, в основном, следующими способами:
· Систематизация информации в виде таблиц
· Представление информации с помощью графических изображений (графиков, диаграмм и пр.)
· Сопровождение текста иллюстрациями в виде фотографий, рисунков, чертежей, схем, карт, рисунков и т.п.
Правила представления приложения:
· все приложения располагаются в конце работы;
· каждое приложение начинается с новой страницы и имеет содержательный заголовок;
· приложения должны иметь общую с остальной частью работы сквозную нумерацию страниц;
· номер приложения размещают в правом верхнем углу над заголовком приложения; после слова «Приложение» знак «№» не ставится;
· на все приложения в основной части работы должны быть ссылки.
Язык работы
Работа должна быть написана чётким и ясным литературным языком, присущим для данного предмета. Сленг и фразы из просторечия не допустимы в исследовательской работе
Раздел11. выполнение моделей пространственных фигур.
Многие наглядные пособия - таблицы, некоторые модели, абаки для индивидуального пользования, палетки, счетный материал, некоторые виды раздаточного материала и т. п. - могут быть сделаны самими учащимися. При изготовлении того или иного пособия, у учащихся неизбежно возникает интерес к нему, появляется желание разобраться в его назначении и математической структуре. А это приводит к лучшему пониманию и лучшему усвоению учебного материала. В ходе работы по изготовлению пособий осуществляются межпредметные связи: с одной стороны, дети применяют свои математические знания и навыки (расчет, измерение, черчение). А с другой- они опираются на навыки, приобретенные на уроках труда (вырезание из бумаги, склеивание и др.)
Приведем примеры наглядных самодельных пособий, которые могут быть выполнены учащимися, и дадим краткое описание способов их изготовления. Все пособия выполняются под руководством или по указанию учителя.
1. Раздаточный материал в виде геометрических фигур, звездочек, рисунков листьев и других предметов может быть изготовлен на листках бумаги или из картона. Для размножения рисунка применяются картонные трафареты или штампы, вырезаемые из сырой картофелины или резины.
2. Домино или лото с картинками. Домино изготовляется из картонных карточек размером, приблизительно 5 х 10 см. и отличается от обычного домино тем, что вместо круглых очков на карточках изображаются группы различных предметов. На карточках лото также изображаются группы предметов. Но здесь они употребляются вместо чисел. Числа на фишках, которыми покрываются карточки, заменяются числовыми фигурами.
Правила игры в домино и лото с картинками обычные. Дети не только учатся считать, но и соотносить между собой численности множеств, состоящих из различных предметов.
3.Абак для индивидуального пользования. Изготавливается из небольшого куска плотной бумаги, разлинованного на три колонки соответственно трем первым числовым разрядам. В каждой колонке прорезается по 10 круглых или квадратных отверстий. Снизу подшивается или подклеивается цветная бумага, чтобы хорошо были видны на фоне ее вырезанные отверстия. Подшитая бумага должна быть, таким образом, чтобы под каждым рядом отверстий оставался небольшой промежуток для узкой картонной полоски. Выдвигая полоски, учащиеся в каждом разряде открывают нужное число отверстий и тем самым показывают заданное многозначное число.
4. Модель циферблата с подвижными стрелками. Деления на круге должны быть нанесены достаточно точно, чтобы учащиеся могли определять показания часов.
5. Модель вехи и экера. Обе эти модели изготавливаются из палочек длиной 12- 23 см. и половинок катушек, которые играют роль подставок. В первом случае палочки раскрашиваются поперечными темными и светлыми полосами, во втором- к торцу палочки прибивается небольшая ( 4 х 4 см ) квадратная дощечка с вбитыми по углам булавками. Используя эти модели, можно провести на внеклассных занятиях подготовку к провешиванию прямых линий и построению прямых углов на местности.
6. Демонстрационные таблицы, схемы, диаграммы.
Для изготовления таких пособий следует широко использовать рисунки из старых книг, журналов, календарей, наклеивая их на большие листы бумаги и дополняя необходимыми линиями и числами. Цифры для изображения чисел могут быть вырезаны из старых перекидных или отрывных календарей.
Знание видов наглядных пособий дает возможность правильно их подбирать и эффективно использовать при обучении. А также изготовлять самому или вместе с детьми необходимые наглядные пособия. Наглядные учебные пособия принято делить на натуральные и изобразительные. К натуральным наглядным пособиям, используемым на уроках математики, относятся предметы окружающей среды. Среди наглядных изобразительных пособий выделяют образные: предметные картинки, изображения предметов и фигур из бумаги и картона, таблицы с изображениями предметов или фигур. К изобразительным наглядным относятся также наглядные экранные пособия, учебные фильмы, диафильмы, диапозитивы.
С точки зрения использования наглядные пособия делят на общеклассные и индивидуальные.
К изготовлению наглядных пособий полезно привлекать детей. Это имеет большое образовательное и воспитательное значение, содействует сознательному и прочному овладению знаниями и умениями, помогает выработке определенных трудовых навыков. Так, изготовляя модель прямого угла из бумаги и модель подвижного угла из двух палочек, скрепленных куском пластилина, ученики получают представление об углах; изготовляя модели линейного и квадратного сантиметра, дециметра, метра, учащиеся получают наглядное представление о единицах длины и площади. Работая с пособиями, изготовленными своими руками, ребенок учится уважительно относиться к труду.
В процессе обучения наглядные пособия используют с различными целями: для ознакомления с новым материалом, для закрепления знаний, умений, навыков, для проверки их усвоения.
Когда наглядное пособие выступает как источник знаний, оно особенно должно подчеркивать существенное- то , что является основой для обобщения, а также показывать несущественное, его второстепенное значение.
Знакомя с новым материалом, нужно использовать наглядное пособие с целью конкретизации сообщаемых знаний. В этом случае наглядное пособие выступает как иллюстрация словесных объяснений.
Например. Помогая детям в поисках решения задачи, нужно сделать схематический рисунок или чертеж к задаче; объясняя прием вычисления, сопровождая пояснение действиями с предметами и соответствующими записями и т. д. При этом важно использовать наглядное пособие своевременно, иллюстрируя самую суть объяснения, привлекая к работе с пособием и пояснению самих учащихся. При раскрытии приема вычисления, измерения, решении задачи и т. д. надо особенно четко показывать движение (прибавить- придвинуть, вычесть - убрать, отодвинуть). Сопровождение объяснения рисунком (чертежом) и математическими записями на доске не только облегчает детям восприятие материала, но и одновременно показывает образец выполнения работы в тетрадях. Например: как расположить чертеж и запись решения в тетради, как обозначить периметр с помощью букв и т. п.
При ознакомлении с новым материалом и особенно при закреплении знаний и умений надо так организовать работу с наглядными пособиями, чтобы учащиеся сами оперировали ими и сопровождали действия соответствующими пояснениями: объединяли множества предметов при изучении сложении, моделировали замкнутые и ломаные незамкнутые линии, пользуясь палочками.
Качество усвоения материала в большинстве случаев значительно повышается, так как в работу включаются различные анализаторы (зрительные, двигательные, речевые, слуховые). При этом дети овладевают не только математическими знаниями. Но и приобретают умения самостоятельно использовать наглядные пособия. Учитель должен всячески поощрять детей к использованию наглядных средств, к самостоятельной работе.
На этапе закрепления знаний и умений необходимо широко использовать для разнообразных упражнений справочные таблицы, таблицы для устного счета, рисунки, схемы, чертежи для составления задач детьми. Для выработки измерительных навыков нужно включать упражнения в черчении и измерении с помощью чертежно- измерительных инструментов. Рекомендуется практиковать ВОСПРОИЗВЕДЕНИЕ НАГЛЯДНО ВОСПРИНЯТОГО ПУТЕМ МОДЕЛИРОВАНИЯ, РИСОВАНИЯ, СЛОВЕСНОГО ОПИСАНИЯ.
Наглядные пособия иногда используют для проверки знаний и умений учащихся. Это делается так: - чтобы проверить, как усвоили дети понятие многоугольник, можно предложить с помощью палочек сложить многоугольник указанного вида. Используя раздаточный дидактический материал, учитель проверяет умения измерять длину отрезков, площадь, периметр многоугольников и др.
Важным условием эффективности использования наглядных пособий является применение на уроке достаточного и необходимого количества наглядного материала. Если наглядные средства применять там, где этого совсем не требуется, то они играют отрицательную роль, уводя детей в сторону от поставленной задачи. Подобные факты встречаются в практике: например, первоклассник обучается выбору арифметического действия при решении арифметических задач. Если привлечь для этой цели картинку, на которой нарисованы птички, сидящие на ветке и подлетающие к ним, ученик, глядя на эту картинку, находит ответ задачи простым пересчитыванием, не выполняя никакого арифметического действия над числами. Наглядность, использованная в этом случае, не только не помогает, но наоборот, задерживает формирование умения решать задачи, т. е. выбирать действие над числами, данными в условии.
Для изготовления ограждений станков, вентиляционных труб и некоторых других изделий вырезают из листового материала их развертки.
Развертка поверхностей любой прямой призмы представляет собой плоскую фигуру, составленную из боковых граней - прямоугольников и двух оснований - многоугольников.
Например, у развертки поверхностей шестиугольной призмы (все грани - равные между собой, прямоугольники с шириной а и высотой h, а основания - правильные шестиугольники со стороной, равной а.
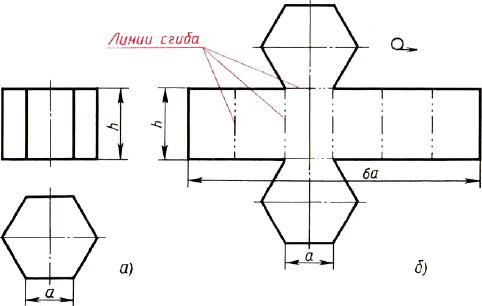
Рис. Построение чертежа развертки поверхностей призмы: а - два вида; б - развертка поверхностей
Таким образом, можно построить чертеж развертки поверхностей любой призмы.
Развертка поверхностей цилиндра состоит из прямоугольника и двух кругов
б). Одна сторона прямоугольника равна высоте цилиндра, другая - длине окружности основания. На чертеже развертки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру оснований цилиндра.
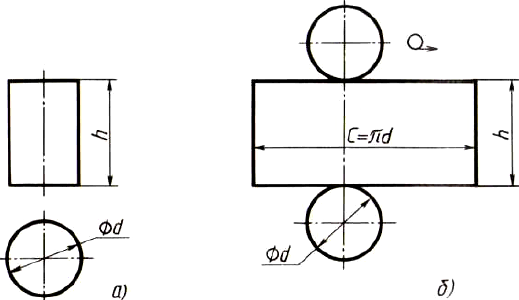
Рис. Построение чертежа развертки поверхностей цилиндра: а - два вида; б - развертка поверхностей
Чертежи разверток поверхностей конуса и пирамиды.
Развертка поверхностей конуса представляет собой плоскую фигуру, состоящую из сектора - развертки боковой поверхности и круга - основания конуса
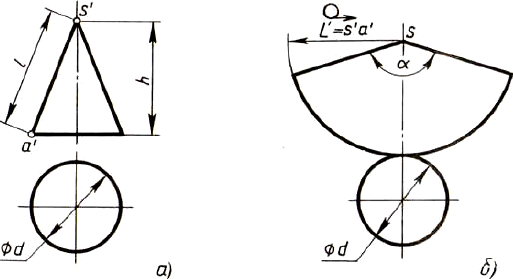
Рис. Построение чертежа развертки поверхностей конуса: а - два вида; б - развертка поверхностей
Построения выполняются так:
-
Проводят осевую линию и из точки s' на ней описывают радиусом, равным длине s'a' образующей конуса, дугу окружности. На ней откладывают длину окружности основания конуса.
Точку s' соединяют с концевыми точками дуги.
-
К полученной фигуре - сектору пристраивают круг. Диаметр этого круга равен диаметру основания конуса.
Длину окружности при построении сектора можно определить по формуле C = 3.14xD.
Угол а подсчитывают по формуле а = 360°хD/2L, где D - диаметр окружности основания, L -длина образующей конуса, ее можно подсчитать по теореме Пифагора.
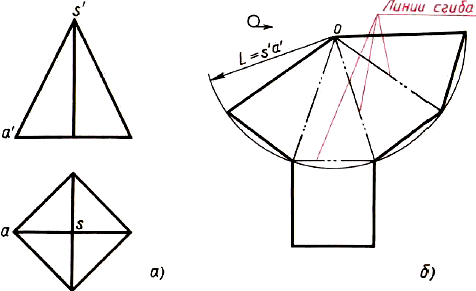
Рис. Построение чертежа развертки поверхностей пирамиды: а - два вида; б - развертка поверхностей
Чертеж развертки поверхностей пирамиды строят так:
Из произвольной точки О описывают дугу радиуса L, равного длине
бокового ребра пирамиды. На этой дуге откладывают четыре отрезка,
равные стороне основания. Крайние точки соединяют прямыми с точкой
О. Затем пристраивают квадрат, равный основанию пирамиды.
Обратите внимание, как оформляют чертежи разверток. Над изображением выносят специальный знак. От линий сгиба, которые проводят штрихпунктирнои с двумя точками, проводят линии-выноски и пишут на полке «Линии сгиба».
ПРИЛОЖЕНИЕ
Самостоятельная работа *Логарифмы* содержит необходимое количество заданий на закрепление и систематизацию знаний и умений по теме. Выполнение некоторых заданий приводит студента к расширению и углублению сферы действий уже полученных знаний. Достаточное количество вариантов обеспечивает индивидуализацию учебного процесса при активной позиции личности студента в учебной деятельности (исключается возможность механического списывания).
Самостоятельная работа прошла апробирование в ходе учебного процесса и доказала свою актуальность.
Актуальность этой методической разработки дает возможность рекомендовать ее к использованию в практике преподавания дисциплины математика не только в системе СПО, но и в общеобразовательной школе в 10 - 11 классах.
Задания по теме * Логарифмы *.
Вариант 2.
1. При каких значениях x имеют смысл выражения:
а)
lg(x + 37) + lg(111 - 2x )
а)
lg (x + 4) + lg(2x - 2)
б)
log x (2x2 - 7x + 6)
б)
log x (3x2 + 16x + 16)
2. Логарифмируйте по основанию a = 7.
2. Логарифмируйте по основанию a = 8.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 7) + log 2(x - 3) = log 211,
а)
log 3(x - 2) + log 3(x + 7) = log 310,
б)
,
б)
,
в)
log2 1/4x + log 1/4x - 6 = 0 .
в)
log2 5x + log 5x - 12 = 0 .
5. Решите неравенства:
5. Решите неравенства:
а)
log 39(39x + 2) ≤1 ,
а)
log 1/6(2x - 2) ≥ 0 ,
б)
log 1/8(2x - 1) + log 1/8x > 0 .
б)
log 4x + log 4(x - 3) < 1
Вариант 3.
Вариант 4.
1. При каких значениях x имеют смысл выражения:.
а)
lg(x + 3) + lg(9 - 2x)
а)
lg(x + 8) + lg(2x - 4)
б)
log x (5x2 - 17x + 14)
б)
log x (4x2 - 13x + 10)
2. Логарифмируйте по основанию a = 3.
2. Логарифмируйте по основанию a = 7.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x - 4) + log 2(x - 5) = log 26 ,
а)
log 3(x - 3) + log 3(x + 6) = log 322 ,
б)
,
б)
,
в)
log2 1/9x - log 1/9x - 2 = 0 .
в)
log2 2x + log 2x - 30 = 0 .
5. Решите неравенства:
5. Решите неравенства:
а)
log 37(37x + 2) ≤1 ,
а)
log 1/5(4x - 2) ≥ 0 ,
б)
log 1/7(2x - 1) + log 1/7x > 0 .
б)
log 6x + log 6(x - 5) < 1 .
Вариант 5.
Вариант 6.
1. При каких значениях x имеют смысл выражение.
а)
lg(x + 5) + lg(15 - 2x)
а)
lg(x + 12) + lg(2x - 6)
б)
log x (4x2 - 9x - 28)
б)
log x (5x2 - 9x - 18)
2. Логарифмируйте по основанию a = 5.
2. Логарифмируйте по основанию a = 2.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 12) + log 2(x-3) = log 216
а)
log 3(x - 5) + log 3(x + 8) = log 3 30
б)
,
б)
,
в)
log2 1/8x + 2log 1/8x - 3 = 0
в)
log2 7x - 2log 7x - 8 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 35(35x + 2) ≤1
а)
log 1/4(6x - 2) ≥ 0
б)
log 1/3(2x - 1) + log 1/3x > 0
б)
log 8x + log 8(x - 7) < 1
Вариант 7.
Вариант 8.
1. При каких значениях x имеют смысл выражение.
а)
lg(x + 7) + lg(21 - 2x)
а)
lg(x + 16) + lg(2x - 8)
б)
log x (3x2 + 4x - 15)
б)
log x (5x2 + 11x - 36)
2. Логарифмируйте по основанию a = 6.
2. Логарифмируйте по основанию a = 4.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 5) + log 2(x - 3) = log 265
а)
log 3(x - 8) + log 3(x + 2) = log 311
б)
,
б)
,
в)
log2 1/5x - log 1/5x - 12 = 0
в)
log2 6x - log 6x - 6 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 33(33x + 2) ≤1
а)
log 1/5(8x - 2) ≥ 0
б)
log 1/9(2x - 1) + log 1/9x > 0
б)
lg x + lg(x - 9) < 1
Вариант 9.
Вариант 10.
1. При каких значениях x имеют смысл выражение.
а)
lg(x + 9) + lg(27 - 2x)
а)
lg(x + 20) + lg(2x - 10)
б)
log x (6x2 + 11x - 21)
б)
log x (4x2 + 23x + 33)
2. Логарифмируйте по основанию a = 3.
2. Логарифмируйте по основанию a = 2.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 11) + log 2(x-4) = log 216
а)
log 3(x - 4) + log 3(x + 6) = log 324
б)
,
б)
,
в)
log2 1/3x - 3log 1/3x - 18 = 0
в)
log2 11x + log 11x - 2 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 31(31x + 2) ≤1
а)
log 0.1(10x - 2) ≥0
б)
log 1/11(2x - 1) + log 1/11x > 0
б)
log 12x + log 12(x - 11) < 1
Вариант 11.
Вариант 12.
1. При каких значениях x имеют смысл выражение.
а)
lg(x + 11) + lg(33 - 2x)
а)
lg(x + 24) + lg(2x - 12)
б)
log x (7x2 - 20x - 32)
б)
log x (2x2 + 5x - 12)
2. Логарифмировать по основанию a = 5.
2. Логарифмировать по основанию a = 2.
3. Найти значение x
3. Найти значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 6) + log 2(x + 3) = log 240
а)
log 3(x - 2) + log 3(x + 7) = log 310
б)
,
б)
,
в)
log2 1/8x - 2log 1/8x - 3 = 0
в)
log2 4x - 2log 4x - 15 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 29(29x + 2) ≤1
а)
log 1/6(12x - 2) ≥0
б)
log 1/13(2x - 1) + log 1/13x > 0
б)
log 14x + log 14(x - 13) < 1
Вариант 13.
Вариант 14.
1. При каких значениях x имеют смысл выражения:
а)
lg(x + 13) + lg(39 - 2x)
а)
lg(x + 28) + lg(2x - 14)
б)
log x (3x2 - 5x - 12)
б)
log x (5x2 - 3x - 26)
2. Логарифмируйте по основанию a = 7.
2. Логарифмируйте по основанию a = 2.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x - 7) + log 2(x + 5) = log 228
а)
log 3(x + 3) + log 3(x - 7) = log 324
б)
,
б)
,
в)
log2 1/2x + 5log 1/2x - 14 = 0
в)
log2 5x - log 5x - 12 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 27(27x + 2) ≤1
а)
log 1/7(14x - 2) ≥0
б)
log 1/15(2x - 1) + log 1/15x > 0
б)
log 16x + log 16(x - 15) < 1
Вариант 15.
Вариант 16.
1. При каких значениях x имеют смысл выражения:.
а)
lg(x + 15) + lg(45 - 2x)
а)
lg(x + 32) + lg(2x - 16)
б)
log x (4x2 - 11x - 20)
б)
log x (3x2 + 2x - 8)
2. Логарифмировать по основанию a = 3.
2. Логарифмировать по основанию a = 6.
3. Найти значение x
3. Найти значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 1) - log 2(x - 3) = log 212
а)
log 3(x - 4) + log 3(x + 2) = log 327
б)
,
б)
,
в)
log2 1/6x + 2log 1/6x - 3 = 0
в)
log2 9x - log 9x - 2 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 25(25x + 2) ≤1
а)
log 1/5(16x - 2) ≥0
б)
log 1/17(2x - 1) + log 1/17x > 0
б)
log 18x + log 18(x - 17) < 1
Вариант 17.
Вариант 18.
1. При каких значениях x имеют смысл выражения:
а)
lg(x + 17) + lg(51 - 2x)
а)
lg(x + 36) + lg(2x - 18)
б)
log x (9x2 - 10x + 1)
б)
log x (3x2 + 11x + 10)
2. Логарифмируйте по основанию a = 4.
2. Логарифмируйте по основанию a = 2.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x - 6) + log 2(x - 7) = log 212
а)
log 3(x - 3) + log 3(x - 5) = log 315
б)
,
б)
,
в)
log2 1/11x + log 1/11x - 2 = 0
в)
log2 8x + log 8x - 6 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 23(23x + 2) ≤1
а)
log 1/9(18x - 2) ≥0
б)
log 1/19(2x - 1) + log 1/19x > 0
б)
log 20x + log 20(x - 19) < 1
Вариант 19.
Вариант 20.
1. При каких значениях x имеют смысл выражения:.
а)
lg(x + 19) + lg(57 - 2x)
а)
lg(x + 40) + lg(2x - 20)
б)
log x (5x2 - 9x - 18)
б)
log x (7x2 - 11x - 30)
2. Логарифмировать по основанию a = 5.
2. Логарифмировать по основанию a = 4.
3. Найти значение x
3. Найти значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x - 1) + log 2(x + 2) = log 228
а)
log 3(x + 4) + log 3(x + 7) = log 370
б)
,
б)
,
в)
log2 1/4x - log 1/4x - 6 = 0
в)
log2 7x + 3log 7x + 2 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 21(21x + 2) ≤1
а)
log 0.1(20x - 2) ≥0
б)
log 1/5(2x - 1) + log 1/5x > 0
б)
log 22x + log 22(x - 21) < 1
Вариант 21.
Вариант 22.
1. При каких значениях x имеют смысл выражения:
а)
lg(x + 21) + lg(63 - 2x)
а)
lg(x + 44) + lg(2x - 22)
б)
log x (4x2 + 5x - 21)
б)
log x (5x2 + 16x + 12)
2. Логарифмируйте по основанию a = 3.
2. Логарифмируйте по основанию a = 6.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x - 8) + log 2(x - 6) = log 23
а)
log 3(x - 4) + log 3(x + 7) = log 326
б)
,
б)
,
в)
log2 1/7x + 5log 1/7x + 6 = 0
в)
log2 2x - log 2x - 30 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 19(19x + 2) ≤1
а)
log 1/5(22x - 2) ≥0
б)
log 1/23(2x - 1) + log 1/23x > 0
б)
log 24x + log 24(x - 23) < 1
Вариант 23.
Вариант 24.
1. При каких значениях x имеют смысл выражения:.
а)
lg(x + 23) + lg(69 - 2x)
а)
lg(x + 48) + lg(2x - 24)
б)
log x (6x2 - 13x - 44)
б)
log x (5x2 - 3x - 26)
2. Логарифмировать по основанию a = 5.
2. Логарифмировать по основанию a = 2.
3. Найти значение x
3. Найти значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 7) + log 2(x - 3) = log 211
а)
log 3(x-11) + log 3(x - 4) = log 318
б)
,
б)
,
в)
log2 1/9x + log 1/9x - 2 = 0
в)
log2 4x + 2log 4x - 15 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 17(17x + 2) ≤1
а)
log 1/3(24x - 2) ≥0
б)
log 1/25(2x - 1) + log 1/25x > 0
б)
log 26x + log 26(x - 25) < 1
Вариант 25.
Вариант 26.
1. При каких значениях x имеют смысл выражения:
а)
lg(x + 25) + lg(75 - 2x)
а)
lg(x + 52) + lg(2x - 26)
б)
log x (6x2 + 19x + 14)
б)
log x (5x2 + 13x - 28)
2. Логарифмируйте по основанию a = 7.
2. Логарифмируйте по основанию a = 4.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 6) + log 2(x + 9) = log 288
а)
log 3(x - 2) + log 3(x + 5) = log 318
б)
,
б)
,
в)
log2 1/5x + log 1/5x - 12 = 0
в)
log2 8x - log 8x - 6 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 15(15x + 2) ≤1
а)
log 1/4(26x - 2) ≥0
б)
log 1/27(2x - 1) + log 1/27x > 0
б)
log 28x + log 28(x - 27) < 1
Вариант 28.
1. При каких значениях x имеют смысл выражения:.
а)
lg(x + 27) + lg(81 - 2x)
а)
lg(x + 56) + lg(2x - 28)
б)
log x (2x2 + 9x + 9)
б)
log x (4x2 + 15x + 14)
2. Логарифмировать по основанию a = 3.
2. Логарифмировать по основанию a = 6.
3. Найти значение x
3. Найти значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 3) + log 2(x + 9) = log 272
а)
log 3(x - 5) + log 3(x + 7) = log 328
б)
,
б)
,
в)
log2 1/6x - 2log 1/6x - 3 = 0
в)
log2 12x + 3log 12x + 2 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 13(13x + 2) ≤1
а)
log 1/5(28x - 2) ≥0
б)
log 1/29(2x - 1) + log 1/29x > 0
б)
log 30x + log 30(x - 29) < 1
Вариант 29.
Вариант 30.
1. При каких значениях x имеют смысл выражения:
а)
lg(x + 29) + lg(87 - 2x)
а)
lg(x + 60) + lg(2x - 30)
б)
log x (3x2 - 7x - 20)
б)
log x (4x2 + 7x - 15)
2. Логарифмируйте по основанию a = 9.
2. Логарифмируйте по основанию a = 6.
3. Найдите значение x
3. Найдите значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 8) + log 2(x + 3) = log 250
а)
log 3(x-12) + log 3(x - 4) = log 333
б)
,
б)
,
в)
log2 1/3x + 3log 1/3x - 18 = 0
в)
log2 11x - log 11x - 2 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 11(11x + 2) ≤1
а)
log 1/6(30x - 2) ≥0
б)
log 1/31(2x - 1) + log 1/31x > 0
б)
log 32x + log 32(x - 31) < 1
Вариант 31.
Вариант 32.
1. При каких значениях x имеют смысл выражения:.
а)
lg(x + 31) + lg(93 - 2x)
а)
lg(x + 64) + lg(2x - 32)
б)
log x (3x2 + 2x - 8)
б)
log x (5x2 + 14x - 24)
2. Логарифмировать по основанию a = 7.
2. Логарифмировать по основанию a = 5.
3. Найти значение x
3. Найти значение x
4. Решите уравнения:
4. Решите уравнения:
а)
log 2(x + 4) + log 2(x - 9) = log 230
а)
log 3(x - 9) + log 3(x - 5) = log 35
б)
,
б)
,
в)
log2 1/7x - 5log 1/7x + 6 = 0
в)
log2 9x - log 9x - 2 = 0
5. Решите неравенства:
5. Решите неравенства:
а)
log 9(9x + 2) ≤ 1
а)
log 1/7(32x - 2) ≥0
б)
log 1/33(2x - 1) + log 1/33x > 0
б)
log 34x + log 34(x - 33) < 1
Ответы к самостоятельной работеВариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
1а
1а
1а
1а
1а
1б
1б
1б
1б
1б
2.
2.
2.
2.
2.
3.
3.
3.
3.
3.
4a
x = 4
4a
x = 3
4a
x = 7
4a
x = 5
4a
x = 4
4б
4б
4б
4б
4б
4в
4в
4в
4в
4в
5а
5а
5а
5а
5а
5б
5б
5б
5б
5б
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
1а
1а
1а
1а
1а
1б
1б
1б
1б
1б
2.
2.
2.
2.
2.
3.
3.
3.
3.
3.
4a
x = 7
4a
x = 8
4a
x = 9
4a
x = 5
4a
x = 6
4б
4б
4б
4б
4б
4в
4в
4в
4в
4в
5а
5а
5а
5а
5а
5б
5б
5б
5б
5б
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
1а
1а
1а
1а
1а
1б
1б
1б
1б
1б
2.
2.
2.
2.
2.
3.
3.
3.
3.
3.
4a
x = 2
4a
x = 3
4a
x = 9
4a
x = 9
4a
x = 5
4б
4б
4б
4б
4б
4в
4в
4в
4в
4в
5а
5а
5а
5а
5а
5б
5б
5б
5б
5б
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
1а
1а
1а
1а
1а
1б
1б
1б
1б
1б
2.
2.
2.
2.
2.
3.
3.
3.
3.
3.
4a
x = 7
4a
x = 10
4a
x = 8
4a
x = 5
4a
x = 3
4б
4б
4б
4б
4б
4в
4в
4в
4в
4в
5а
5а
5а
5а
5а
5б
5б
5б
5б
5б
Вариант 21
Вариант 22
Вариант 23
Вариант 24
Вариант 25
1а
1а
1а
1а
1а
1б
1б
1б
1б
1б
2.
2.
2.
2.
2.
3.
3.
3.
3.
3.
4a
x = 9
4a
x = 6
4a
x = 4
4a
x = 13
4a
x = 2
4б
4б
4б
4б
4б
4в
4в
4в
4в
4в
5а
5а
5а
5а
5а
5б
5б
5б
5б
5б
Вариант 26
Вариант 27
Вариант 28
Вариант 29
Вариант 30
1а
1а
1а
1а
1а
1б
1б
1б
1б
1б
2.
2.
2.
2.
2.
3.
3.
3.
</<br>
3.
3.
4a
x = 4
4a
x = 3
4a
x = 7
4a
x = 2
4a
x = 15
4б
4б
4б
4б
4б
4в
4в
4в
4в
4в
5а
5а
5а
5а
5а
5б
5б
5б
5б
5б
Вариант 31
Вариант 32
1а
1а
1б
1б
2.
2.
3.
3.
4a
x = 11
4a
x = 10
4б
4б
4в
4в
5а
5а
5б
5б
Литература
-
Математика для техникумов. Алгебра и начала анализа /Под ред. Г.Н.Яковлева - М.: «Наука», 1987.-Ч.1
-
Математика для техникумов. Алгебра и начала анализа /Под ред. Г.Н.Яковлева - М.: «Наука», 1988.-Ч.2.
-
М.И. Башмаков Математика (базовый уровень). 10-11 кл. - М., 2005.
-
Н.В.Богомолов Практические занятия по математике: Учебное пособие, 5 изд. - М.: «Высшая школ», 2008.
-
Коджаспирова Г.М., Коджаспиров А.Ю. Словарь по педагогике. - Москва: ИКЦ «МарТ»; Ростов н/Д: Издательский центр «МарТ», 2005. - 448 с.
-
Темербекова А.А Методика преподавания математики: Учеб. пособие для студ. высш. учеб. Заведений. - М.: Гуманит. изд. центр ВЛАДОС, 2003. - 176с.