- Учителю
- Конспект урока в соответствии с требованиями технологии развития критического мышления по теме: Окружность. Взаимное расположение прямой и окружности
Конспект урока в соответствии с требованиями технологии развития критического мышления по теме: Окружность. Взаимное расположение прямой и окружности
КОНСПЕКТ УРОКА В СООТВЕТСТВИИ С ТРЕБОВАНИЯМИ
ТЕХНОЛОГИИ КРИТИЧЕСКОГО МЫШЛЕНИЯ
Стифоровой А.А.
Тема урока: «Окружность. Взаимное расположение прямой и окружности»
Предмет: геометрия
Класс: 8
Цель урока:
1. Дать определения понятиям: окружность, центр окружности, радиус, диаметр, хорда.
2. Изучить возможности взаимного расположения прямой и окружности.
Планируемые образовательные результаты:
предметные
-
знать определения понятий: окружность, центр окружности, радиус, диаметр, хорда;
-
знать возможности взаимного расположения прямой и окружности
личностные
-
развитие познавательных интересов, учебных мотивов;
-
проявление дисциплинированности, трудолюбия и упорства в решении поставленных целей;
метапредметные
-
умение ставить перед собой цель и планировать деятельность в соответствии с поставленной целью;
-
сличение способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
-
умение вступать в сотрудничество с учителем и сверстниками, работать в группе;
-
формирование научного мировоззрения
Тип урока: урок открытия нового знания
Формы работы учащихся: фронтальная, индивидуальная, групповая (парная).
Оборудование: компьютер, проектор (для физкультминутки), доска, распечатанные приложения.
Учебник: Атанасян Л.С. Геометрия 7-9, 2014 г.
Структура и ход урока:
№
Этап урока
Деятельность учителя
Деятельность обучающихся
Время
Формируемые УУД.
1
Организационный момент. Мотивация к учебной деятельности.
Приветствует учащихся; проверяет готовность класса к уроку; организует внимание.
- Тема сегодняшнего урока: «Окружность. Взаимное расположение прямой и окружности».
Откройте тетради, запишите число и тему.
Приветствие
учащихся. Эмоционально настраиваются на работу, включаются в деловой ритм урока.
Записывают число и тему урока в тетрадь.
1
Регулятивные:
- организация своей учебной деятельности
- прогнозирование своей деятельности
Коммуникативные:
- планирование учебного сотрудничества
Личностные:
- волевое усилие, самоорганизация
2
Актуализация знаний
Фронтальная работа.
- Ребята, давайте вспомним, что такое окружность, и какие у нее есть элементы.
Работа с таблицей из Приложения 1 (На парте лист с приложением 1).
Используя опорные слова, иллюстрации, сформулируйте определения.
- Итак, что такое окружность? радиус? хорда? диаметр?
Задача. Радиус окружности равен 5 см. Найдите расстояние от центра окружности до прямой, содержащей хорду, равную 8 см.
Решение может приводить и учитель на доске, слушая мнения учащихся.
(При изложении материала в учебнике используют общее решение. Учащиеся будут работать с материалом учебника самостоятельно, для лучшего усвоения предлагаю эту задачу).
- Что является расстоянием от центра окружности до прямой, содержащей хорду?
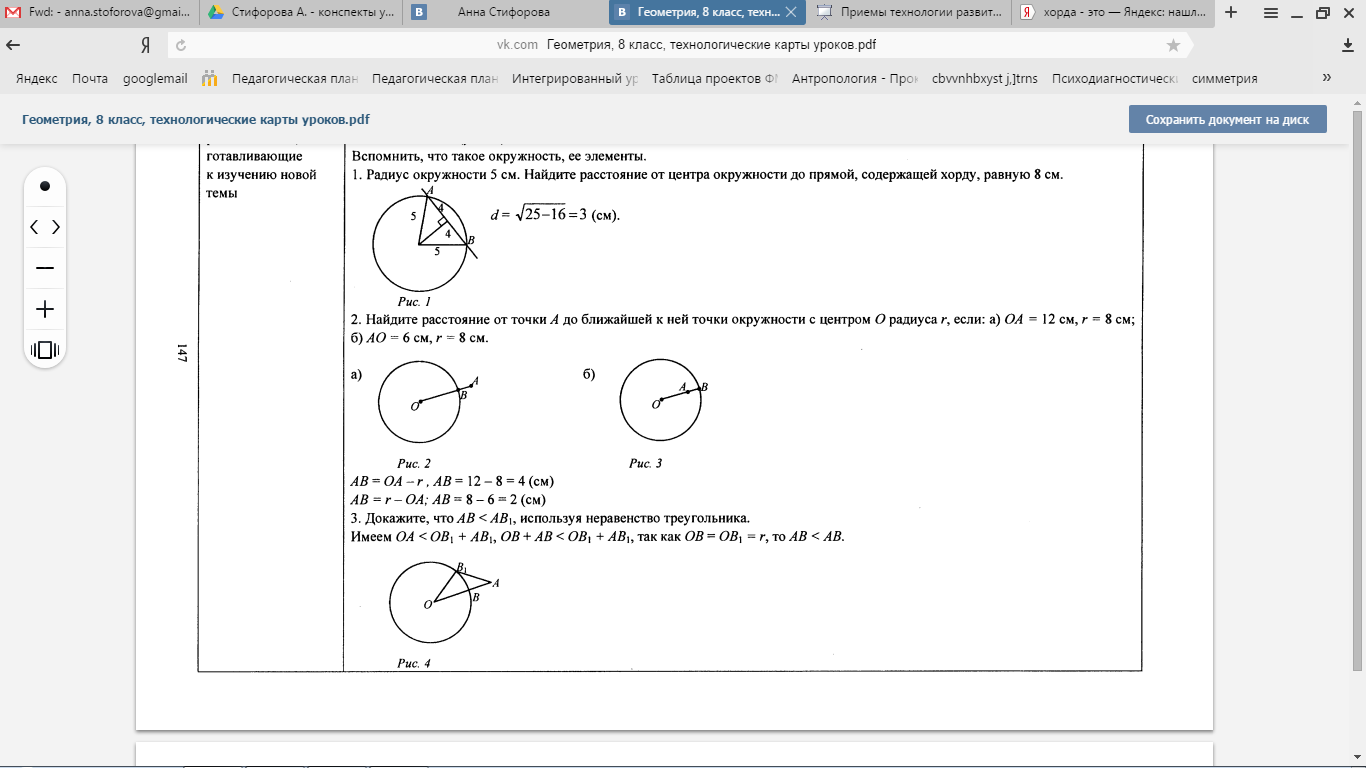
Задача. Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О и радиуса r, если а) ОА=12 см, r=8 см, б) ОА=6 см, r=8 см.
- Где будет лежать ближайшая точка?
Работают с таблицей. Формулируют определения, обсуждают с классом.
Окружность - фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности.
Радиус - отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
Хорда - отрезок, соединяющий две точки окружности.
Диаметр - хорда окружности, проходящая через ее центр
Решают задачу с учителем.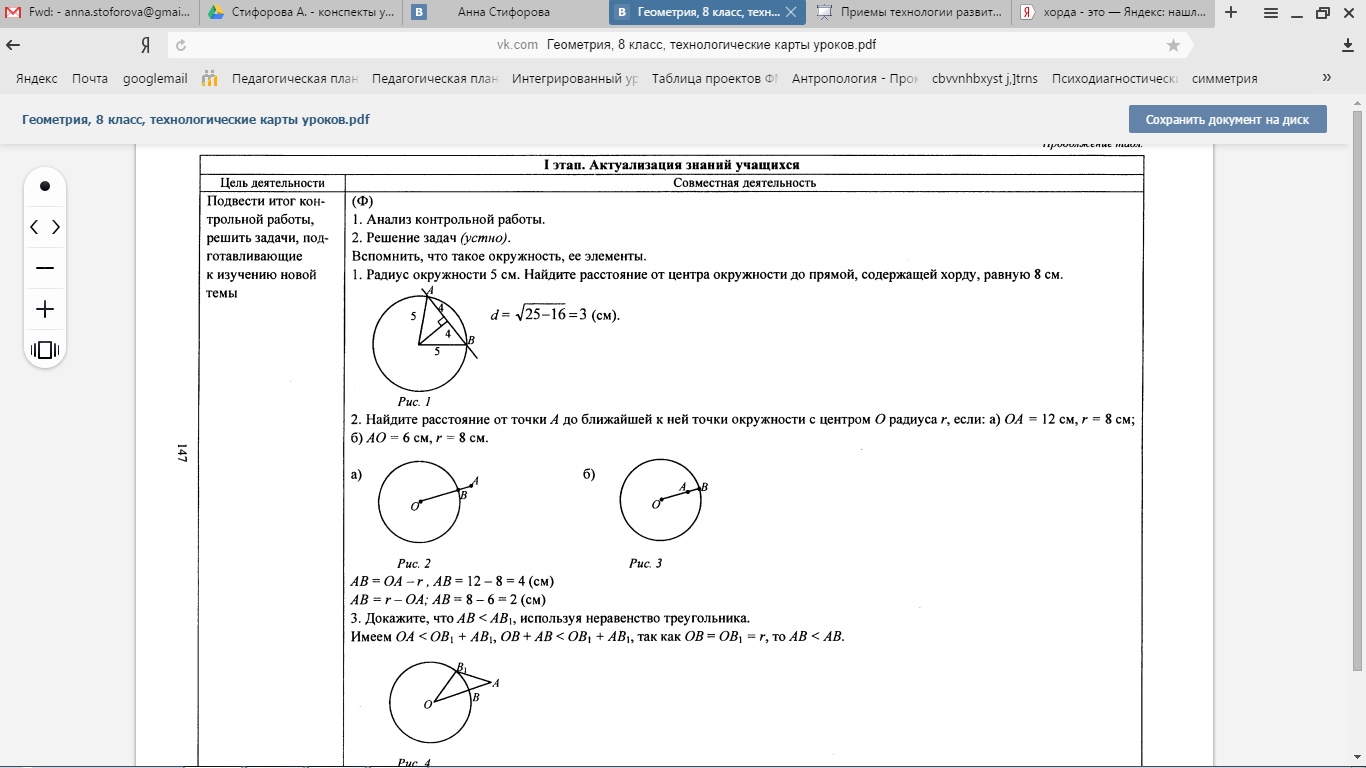
Длина перпендикуляра, опущенного из центра окружности до прямой, содержащей хорду АВ.
О - центр, Н - основание перпендикуляра.
(Проводим перпендикуляр, получаем прямоугольный треугольник ОНА, по теореме Пифагора находим искомое расстояние. Учитывая, что данный перпендикуляр (высота в треугольнике) разбивает АВ на два равных отрезка (треугольник ОАВ равнобедренный, высота, опушенная из вершины, является медианой))
Решают задачу с учителем.
- Блажайшая точка будет лежать на одной прямой с т. А и О.
7
Регулятивные:
- планирование своей деятельности для решения задач
- умение осуществлять контроль своей деятельности в процессе достижения результата
Коммуникативные:
- слушать и вступать в диалог
Познавательные:
- создавать и преобразовывать модели и схемы для решения задач
- излагать известную информацию в контексте поставленного вопроса
2
Постановка проблемы и ее решение.
Стадия вызова
Цель: побудить к работе с новой информацией, вызвать интерес к новой теме.
Прием: «Верю - не верю»
Учитель предлагает заполнить таблицу см. в Приложении 2 (у каждого учащегося на парте лист с Приложением 2).
- Ребята, как вы думаете, каковы будут цели сегодняшнего занятия?
Учитель помогает сформулировать цели урока
Ребята заполняют каждый сам таблицу, отмечая во что они верят и не верят.
Формулируют цели занятия:
1. Узнать определения понятиям: окружность, радиус, диаметр, хорда.
2. Изучить возможности взаимного расположения прямой и окружности.
3
Регулятивные:
- постановка цели учебной задачи
Коммуникативные:
- слушать и вступать в диалог;
- умение выражать свои мысли в письменной и устной форме
Познавательные:
- создавать и преобразовывать модели и схемы для решения задач
- излагать известную информацию в контексте поставленного вопроса
3
Изучение нового материала
Стадия осмысления
Цель: получить новую информацию по теме, сохранить интерес к изучаемой теме.
Прием: Таблица вопросов
(На парте лист с приложением 3)
Учитель предлагает учащимся ознакомиться с исторической справкой по теме Приложение 3.
- Что нового вы узнали? Сравните материал с вашими ответами на вопросы «Верю - не верю»
- Опираясь на таблицу вопросов, составьте устно по 1 вопросу на каждое вопросительное слово.
(Работа в парах) Задайте вопрос соседу по парте и ответьте на его вопрос.
- Практическая работа с Приложением 4.
Учащиеся выполняют самостоятельно. По ходу учитель координирует и проверяет построения.
Обсудите свои выводы с соседом по парте.
Знакомятся с исторической справкой. Сравнивают материал с ответами на вопросы «Верю - не верю», составляют по 1 вопросу на каждое вопросительное слово из таблицы (устно), задают его соседу по парте, отвечают на вопрос соседа.
Самостоятельная практическая работа.
10
Регулятивные:
- планирование своей деятельности для решения задач
- умение осуществлять контроль своей деятельности в процессе достижения результата
Коммуникативные:
- слушать и вступать в диалог
- умение работать в группе
Познавательные:
- создавать и преобразовывать модели и схемы для решения задач
- сравнивать, обобщать и делать выводы
- формирование научного мировоззрения
4
Физкульт-ка
Выполняя умственную работу необходимо расслабляться. Давайте немного отдохнем.
Физкультминутка</<font color="#000000"> - 2 мин
Выполняют упражнения физкультминутки
2
Личностные:
- осознание ценности здоровья
5
Первичное осмысление и закрепление знаний
Учитель обсуждает с классом выполнение практической работы.
- Сколько общих точек может иметь окружность и прямая?
Прием: Инсерт
- Ознакомьтесь с материалом в учебнике п.68, стр. 162, проставьте значки в тексте:
V - уже знал;
+ - новое;
- - думал иначе или не знал
? - не понял, есть вопросы.
- Задайте вопросы, если они есть.
- Чем по отношению к окружности является прямая, если она имеет с ней 2 общие точки?
- Если прямая и окружность не имеют общих точек? Пресекает ли прямая эту окружность?
- В случае, когда прямая с окружностью имеют 1 общую точку, прямая называется касательной, а их общая точка - точка касания. Об этом мы поговорим на следующем занятии.
Учащиеся обсуждают полученные результаты, устраняют ошибки в тетрадях.
Либо 2 общие точки, либо 1 общую точку, либо не иметь общих точек вообще.
Учащиеся работают с материалом учебника, проставляют значки и задают вопросы при необходимости.
Секущей
Прямая и окружность не пересекаются
7
Регулятивные:
- планирование своей деятельности для решения задач
- умение осуществлять контроль своей деятельности в процессе достижения результата
- умение корректировать свои действия в соответствии с изменяющейся ситуацией
Коммуникативные:
- слушать и вступать в диалог
Познавательные:
- сравнивать, обобщать и делать выводы
- поиск и выделение необходимой информации
6
Закрепление изученного на уроке
Решение задач из учебника.
№ 631 (а, г, д) - устно.
Желающие по цепочке.
Пусть d - расстояние от центра окружности радиуса r до прямой p. Каково взаимное расположение прямой p и окружности, если:
а) r=16 см, d=12 см;
г) r=8 см, d=1,2 дм;
д) r=5 см, d=50 мм;
№ 632
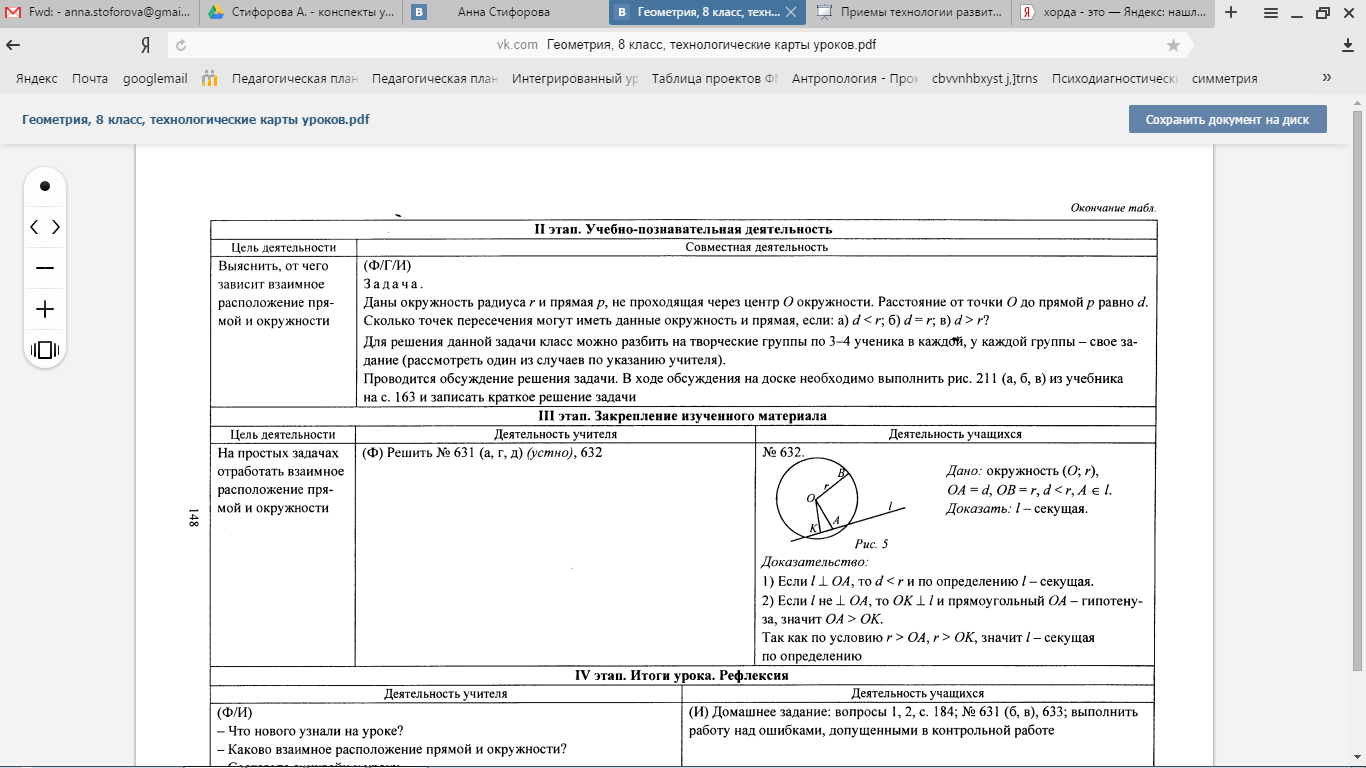
Расстояние от точки А до центра окружности меньше радиуса окружности. Докажите, что любая прямая, проходящая через точку А, является секущей по отношению к данной окружности.
Фронтальная работа над решением задачи. Можно вызвать учащихся сделать построение, написать дано.
- Как могут располагаться прямая l и ОА? Что имеем в каждом случае?
Решают № 631 (а, г, д) устно
а) d< r - окружность и прямая имеют две общие точки.
г) d> r - окружность и прямая не имеют общих точек.
д) d= r - прямая и окружность имеют одну общую точку.
№ 632
10
Регулятивные:
- планирование своей деятельности для решения задач
- умение осуществлять контроль своей деятельности в процессе достижения результата
Коммуникативные:
- адекватно понимать причины успеха и неудач
- умение выражать свои мысли с достаточной полнотой и четкостью
Познавательные:
- создавать и преобразовывать модели и схемы для решения задач
- сравнивать и делать выводы
- поиск и выделение необходимой информации;
- излагать новую информацию в контексте поставленного вопроса
7
Итог урока. Рефлексия.
Стадия рефлексии
Цель: соотнесение новой информации и полученных знаний, выработка собственной позиции, оценка процесса.
- Достигнуты ли цели, поставленные нами в начале урока?
- Что нового вы узнали на уроке?
- Как могут располагаться прямая и окружность?
Прием: Синквейн
Придумать синквейн по теме урока.
Учащиеся проговаривают ещё раз взаимное расположение прямой и окружности, отвечают на вопросы.
3
Регулятивные:
- оценка своей деятельности в рамках урока
Коммуникативные:
- умение слушать и вступать в диалог
Познавательные:
- умение строить речевое высказывание в устной и письменной форме
- рефлексия деятельности
8
Домашнее задание
Учитель задает дозированное домашнее задание, дает рекомендации по его выполнению.
Учебник:
п. 70, вопросы 1,2 ст. 184,
№ 631 (б,в), № 633 смотри записи в тетради.
Учащиеся записывают домашнее задание, обсуждают, задают вопросы учителю при необходимости.
2
Регулятивные:
- ставить перед собой цель и панировать деятельность
Коммуникативные:
- умение слушать
Приложение 1.
Определение понятий
Приложение 2.
Прием «Верю - не верю»
Вопросы по теме
"-" не верю
1. Верите ли вы, что самая простая из кривых линий - окружность?
2. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова?
3. Верите ли вы, что впервые термин "радиус" встречается лишь в 16 веке?
4. Верите ли вы, что в переводе с латинского радиус означает "луч"?
5. Верите ли вы, что при заданном периметре именно окружность ограничивает наибольшую площадь?
6. Верите ли вы, что в русском языке слово "круглый" означает высшую степень чего-либо?
7. Верите ли вы, что выражение "ходить по кругу" когда-то означало "прогресс"?
8. Верите ли вы, что хорда в переводе с греческого означает "струна"?
9. Верите ли вы, что определение "касательной" уже есть в первом учебнике геометрии - "Начала" Евклида?
Приложение 3.
Историческая справкаСамая простая из кривых линий - окружность. Это одна из древнейших геометрических фигур. Ещё вавилоняне и древние индийцы считали самым важным элементом окружности - радиус. Слово это латинское и означает "луч". В древности не было этого термина: Евклид и другие учёные говорили просто "прямая из центра", Ф. Виет писал что "радиус" - это "элегантное слово". Общепринятым термин "радиус" становится лишь в конце XVII в. Впервые термин "радиус" встречается в "Геометрии" французского ученого Рамса, изданной в 1569 году.
В Древней Греции круг и окружность считались венцом совершенства. Действительно в каждой своей точке окружность "устроена" одинаково, что позволяет ей как бы двигаться "по себе". На плоскости этим свойством обладает еще лишь прямая. Одно из интереснейших свойств круга состоит в том, что он при заданном периметре ограничивает максимальную площадь.
В русском языке слово "круглый" тоже стало означать высокую степень чего-либо: "круглый отличник", "круглый сирота" и даже "круглый дурак".
Если вы когда-либо пробовали получить информацию от бюрократической организации, вас, скорее всего "погоняли по кругу". Фраза "ходить по кругу" обычно не ассоциируется с прогрессом. Но в период индустриальной революции, выражение "ходить по кругу" очень точно отражало прогресс. Шкивы и механизмы давали машинам возможность увеличить производительность и значит сократить рабочую неделю.
Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас. Окружности и циклы идут, взявшись за руки. Циклы получаются при движении по кругу. Мы изучаем циклы земли, они помогают нам разобраться, когда надо сажать растения и когда мы должны вставать.
Представление об окружности даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса, спицы которого соответствуют радиусам окружности.
Термин "хорда" (от греческого "струна") был введён в современном смысле европейскими учёными в XII-XIII веках.
По материалам книг: Г. Глейзер "История математики в школе", С Акимова "Занимательная математика".
Таблица вопросов
Практическая работа
Постройте прямую m, отметьте точку М, не лежащую на данной прямой, проведите отрезок МК, перпендикулярный прямой m.
Постройте в тетради три окружности с центром в точке М, так чтобы:
1. Радиус окружности r < MK
2. Радиус окружности r = MK
3. Радиус окружности r >MK
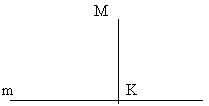
Сделайте вывод о взаимном расположении прямой и окружности, в зависимости от радиуса и расстояния от центра до прямой (сколько общих точек имеют прямая и окружность в каждом случае?).
Постройте в тетради таблицу, заполните ее.
12