- Учителю
- Обобщающий урок по геометрии на тему Площади (8 класс)
Обобщающий урок по геометрии на тему Площади (8 класс)
МАОУ «Свободненская СОШ»
</<br>
Конспект урока по теме «Площади»
(Геометрия 8 класс)
Учитель математики
Алеевская Татьяна Петровна
2016 год
Урок геометрии в 8 классе по теме «Площади» - урок обобщения.
Цели урока:
Обучающие:
-
обобщение и систематизация знаний учащихся по данной теме;
-
усиление прикладной и практической направленности изученной темы.
Развивающие:
-
расширение кругозора учащихся,
-
пополнение словарного запаса,
-
pазвитие коммуникативных навыков общения,
-
pазвитие умений организации учебного труда.
Воспитательные:
-
воспитание интереса к предмету.
Оборудование: компьютер, интерактивная доска, раздаточный материал (карточки с заданиями), презентация.
План урока:
-
Организационный момент.
-
Проверка домашнего задания.
-
Графический диктант.
-
Математическая эстафета
-
Физкультминутка
-
Работа по решению уровневых задач.
-
Выставление оценок.
-
Итог урока.
Ход урока.
1. Организационный момент: проверить готовность класса к уроку, просмотреть наличие учебников, тетрадей, чертёжных инструментов.
2. Проверка домашнего задания: решение дополнительной домашней задачи заранее подготавливается на доске.
3. Тест.
Каждое задание оценивается в 1 балл.
1. Выберите верное утверждение:
а) площадь прямоугольника равна произведению двух его соседних сторон;
б) площадь квадрата равна квадрату его стороны;
в) площадь прямоугольника равна удвоенному произведению двух его сторон.
2. Выберите верное утверждение:
а) площадь ромба равна произведению его диагоналей; б) площадь ромба равна половине произведения его сторон;
в) площадь ромба равна половине произведения его стороны и высоты, проведенной к ней.
3. По формуле S = a · ha можно вычислить площадь: а) ромба; б) параллелограмма;
в) треугольника.
4.Площадь прямоугольного треугольника равна:
а) половине произведения его стороны на какую-либо высоту; б) половине произведения его катетов;
в) произведению его стороны на проведенную к ней высоту.
5. Площадь трапеции ABCD с основаниями AB и CD и высотой BH вычисляется по формуле:
а) S = AB:2· CD· BH; б) S = · BH
в) S = ·BH.
6. Площадь параллелограмма равна произведению:
а) двух его соседних сторон; б) его стороны на высоту, проведённую к этой стороне;
в) половине произведения его стороны на высоту, проведённую к этой стороне;
7. По формуле S = d1· d2 можно вычислить площадь:
а) ромба; б) параллелограмма;
в) треугольника.
8. Площадь треугольника равна:
а) половине произведения его сторон; б) половине произведения его стороны на какую-либо высоту;
в) половине произведения его стороны на проведенную к ней высоту.
9. Выберите верное утверждение:
а) площадь прямоугольника равна произведению двух его противолежащих сторон;
б) площадь квадрата равна произведению его всех сторон;
в) площадь прямоугольника равна произведению двух его соседних сторон.
10. Выберите формулу для нахождения площади трапеции:
а) S = ; б) S = ·h
в) S = d1· d2
Проверка
2
3
4
5
6
7
8
9
10
Ответ
а, б
б
а, в
б
в
б
а
в
в
б
4. Математическая эстафета.
Решение задач по готовым чертежам проходит в виде эстафеты. На слайде нарисованы геометрические фигуры, написано условие задачи. Учащиеся разбиты на две команды. Задачи решают на местах и по очереди на доске пишут ответы. Одна задача - один балл.
1. 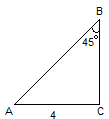 2.
2.
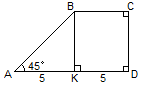 3.
3.
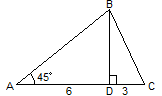
4.  5.
5.
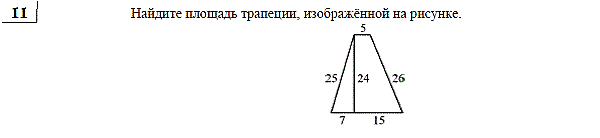 6.
6.
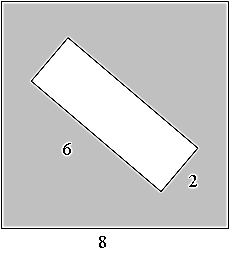
7. 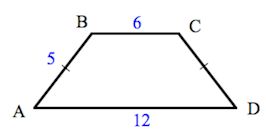 8.
8.

5. Физкультминутка. Гимнастика для глаз.
6. Самостоятельная работа с последующей проверкой на доске.
На партах разложены карточки двух вариантов. Задачи разной степени сложности для самостоятельного решения. Учащиеся меняются тетрадями и проводят взаимопроверку.
Каждое задание по 1 баллу. Задания, написанные курсивом по 2 балла.
Ответы
Решение задачи на доске.
Дан прямоугольник ABCD. AB = 20см, BC = 12см. Середины соседних сторон соединены отрезками. Найти площадь получившегося четырёхугольника.
7. Выставление оценок.
8. Подведение итогов урока.
9. Задание на дом: вопросы для повторения к главе 4 на стр. 133-134: № 518 (по желанию).
Карточки:
-
В треугольнике АВС площадь равна 60 см2 , стороны равны 5 см и 6 см. Найдите высоты, проведенные к этим сторонам.
-
Сторона треугольника равна 10 см, а высота, проведенная к ней равна 8 см. Найти высоту треугольника, проведенную к стороне, равной 16 см.
-
Основания трапеции равны 13 см и 27 см, а высота, проведенная к основаниям, равна 8 см. Вычислите площадь треугольника.
4. Катеты прямоугольного треугольника равны 15 см и 8 см. Вычислите гипотенузу и площадь треугольника.
5. Найти стороны параллелограмма, если его высоты равны 20 см и 25 см, Площадь параллелограмма равна 100 см2.