Практическая работа по математике для 11 класса 'Вычисление пределов'

Максимова Р.П.

Иркутский авиационный техникум

Практическая работа по теме: Теория пределов.

Цель: Научить вычислять пределы , раскрывать неопределённости, используя свойства, теоремы и 2 замечательных предела

Задачи: 1. Проверить понимание темы «Теория пределов»

2. Проверить умение использовать свойства и теоремы о пределах и вычислять пределы и применяя теорию пределов для решения физических задач

Оборудование: Ноутбуки, компьютеры, учебник Омельченко В.П., Э.В.Курбатова - Математика: уч.пособие - изд8-е - Ростов н/Д: Феникс, 2013.- 320 с - (Среднее профессиональное образование)

Формирование компетенций ОК 2, ОК 6:

ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями
Подготовка к работе

1. Повторить основные понятия и определения по учебнику Математика / Омельченко В.П. с. 73 - 85

2. Просмотреть презентацию по теме «Теория пределов»:

Основные теоремы о пределах

(1)

(1*), то из условий(1) и (1*) 

(2) lim (x^m) = (lim x)^m (3) (4)

lim, если limy0(5) lim (log_a x) = log_a (lim x) (6)

Запомните, что

lim = 1, при х 0 (Первый замечательный предел)

lim ⁿ = e, при n   - число е; е  2,71828 - основание натуральных логарифмов; (логарифм числа х по основанию е называется натуральным

логарифмом и обозначается ln x.

; ( второй замечательный предел)

При х ; или при  0.

2. Рассмотрите решение следующих примеров:

Пример 1. Найти lim (x⁴ - 3x² + 16x + 1), при х -1

Решение. lim (x⁴ - 3x² + 16x + 1) = (lim x⁴ - lim 3x² + 16x + 1) = [(lim x)⁴ - 3(lim x)² +16lim x +1] =

=(-1)⁴ - 3(-1)² + 16(-1) + 1 = -17 Ответ. - 17.

Примечание. Для нахождения предела целого или дробного рационального алгебраического выражения, если предел знаменателя не равен нулю, надо переменную x заменить ее пределом и произвести указанные в выражении действия. Например,

Пример 2. Найти

Решение. Применить теорему о пределе дроби (частного) нельзя, т.к. при х0

lim (5х³ -3х²)=0

До перехода к пределу следует упростить данную дробь:

Предел знаменателя

-3  0

Применяя теперь теорему о пределе дроби (частного), получим:

Ответ. -2/3

Пример 3: Найти

Решение. 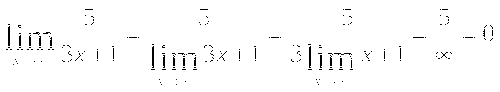Ответ. 0.

Пример 4. Найти

Решение. Числитель и знаменатель дроби превращаются в бесконечность, а их отношение не имеет смысла. Поэтому преобразуем дробь, разделив числитель и знаменатель дроби на наивысшую степень аргумента, т.е. на х³.

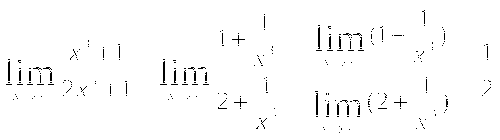Ответ. 1/2.

Пример 5. Найти

Решение. Применить теорему о пределе дроби нельзя, т.к. предел знаменателя равен нулю.

Перепишем данное выражение так:

, Применяя формулу , получим: Ответ. 4.

Пример 6. Найти

Решение. применить теорему о пределе частного нельзя, т.. при х=5 числитель и знаменатель обращаются в нуль. Перепишем данную дробь в виде

,

Переходя к пределу, получим:

Ответ.

3. Вычисление пределов и раскрытие неопределенностей вида .

Самостоятельно решить задачи и вычислить пределы:

1. При параллельном соединении двух проводников, имеющих сопротивления r и r' , общее сопротивление R, соответствующей части электрической цепи, вычисляется по формуле

Считая r известным, найти

Истолкуйте полученные результаты с точки зрения физики.

2. Формула выпуклой линзы имеет вид:

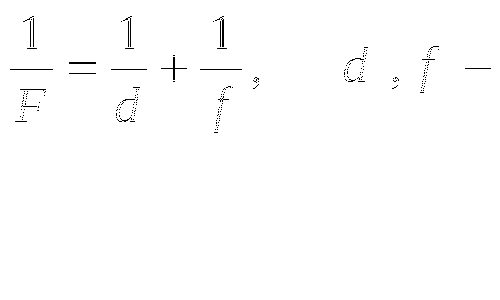Расстояния соответственно предмета и его изображения. - фокусное расстояние линзы (const); найти ; полученные результаты объяснить с точки зрения физики.

4. Вычислить следующие пределы:

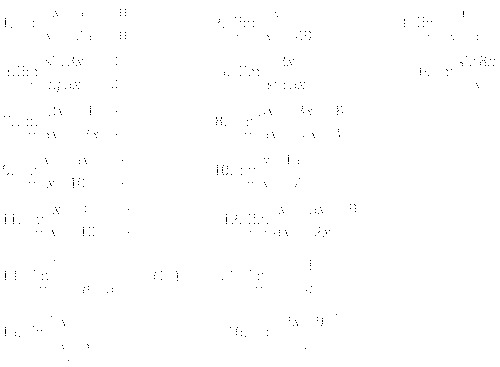Итог занятия

Оформить отчет и сдать на проверку

Домашнее задание. Решить (на выбор ) любые 2задачи с последующим объяснением на занятиях

1. Масса движущегося тела определяется соотношением - отношение скорости тела к скорости света. Покажите, что в предельном переходе при 0 массу можно считать постоянной и равной m_о.

2. Интервал времени между двумя событиями зависит от скорости движения системы,

где эти события происходят, следующим образом:

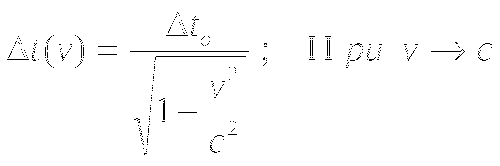найдите предел функции t(v) и сделайте вывод, считая, например, что tо - продолжение жизни близнеца, оставшегося на Земле, а t - продолжительность жизни его брата, отправившегося в космическое путешествие.

3.Значение кинетической энергии тела выражается формулой

Найдите предел этой функции,

т.е. получите классическую формулу для кинетической энергии, если .

4.Сила давления летчика, cовершающего «мертвую петлю», на сиденье в момент достижения верхней точки «мертвой петли» выражается формулой   m (a - g), где a= v²/r - центростремительное (нормальное) ускорение , r- радиус петли. Рассматривая данные выражения как функцию центростремительного ускорения, докажите, что при предельном переходе аg летчик испытывает состояние невесомости.

5.Сила давления летчика на сиденье в нижней точке «мертвой петли» определяется формулой Q=m(g + v²/r), m- масса летчика, g = 9,8 м/с².

Рассматривая данное выражение как функцию от r , найдите ее предел при: а) r; b) r 0. Сделайте соответствующие выводы.

6.В падающем с ускорением а лифте тело давит на пол кабины с силой P= m(а - g), g - ускорение свободного падения. Рассматривая данный процесс как функцию от а, найдите ее предел при а) ag; b) a 0.

Сделайте выводы.

Таблица ответов

№

Зада-

ния

1 задача

2 задача

3 задача

4 задание

1

2

3

4

5

6

7

Максимальное количество баллов

3

3

3

1

1

1

2

2

2

2

Набранные баллы

4 задание

№

Зада-ния

8

9

10

11

12

13

14

15

16

Сумма баллов

Максимальное количество баллов

2

2

2

2

2

3

3

4

4

44

Набранные баллы

Таблица перевода баллов в оценку

Набранное количество баллов

Оценка

0 - 15

2 (неудовлетворительно)

16 - 30

3 (удовлетворительно)

31 - 38

4 (хорошо)

39 - 44

5(отлично)