Департамент образования, науки и молодежной политики Воронежской области

государственное бюджетное профессиональное образовательное учреждение Воронежской области

«Воронежский политехнический техникум»

(ГБПОУ ВО «ВПТ»)

Методическая разработка урока с использованием

компьютерных технологий на тему

Геометрические приложения определенного интеграла.

Дисциплина: Математика

для специальностей: 19.02.10 Техническое обслуживание и ремонт автомобильного транспорта

Разработал:

преподаватель: Ткаченко Л.Н.

г. Воронеж, 2016 г.

Тема урока: Геометрические приложения определенного интеграла.

Цель и задачи урока:

1. Образовательная: Ознакомление учащихся с геометрическим смыслом определенного интеграла, формулами для нахождения площади фигуры и объема тела вращения, формирование умения решать простейшие задачи на нахождение площадей и объемов..

2. Воспитательная: воспитание у учащихся стремления к расширению полученных знаний, формирование активности, умения работать самостоятельно.

3. Развивающая: развитие умения делать выводы и обобщение, учить применять ранее изученный материал для работы по новой теме; активизация познавательной деятельности.

Методическое обеспечение

1. Компьютерные слайды

2. Таблицы основных интегралов, свойств определенного интеграла.

План урока

1. Организационный момент - 3 мин.

2. Проверка домашнего задания - 6 мин.

3. Изложение нового материала с поэтапным закреплением - 60 мин.

4. Задание на дом - 4 мин.

5. Подведение итогов, выставление оценок - 7 мин.

Ход урока

1 Организационный момент: подготовка группы к уроку, отметка отсутствующих.

2 Проверка домашнего задания.

Вариант 11 - у доски, варианты 10, 12 - фронтально. Опрос таблицы интегралов, свойств определенного интеграла - по карточкам.

Вариант 11. Найти неопределенный интеграл:

1) ; 2) ; 3) .

Вариант 12. Найти неопределенный интеграл:

1) ; 2) ; 3) .

Вариант 13. Найти неопределенный интеграл:

1) ; 2) ; 3)

3 Изложение нового материала с поэтапным закреплением.

Тема сегодняшнего занятия - «Геометрические приложения определенного интеграла».

1. Вычисление площадей. (слайд 2)

Определение. Фигура, ограниченная графиком функции, осью абсцисс и прямыми х = а, х = b, называется криволинейной трапецией (слайд 3).

Вычисление площади такой фигуры выполняется с помощью определенного интеграла по формуле Ньютона - Лейбница:

(слайд 5,4).

Задача № 1. Вычислить площадь фигуры, ограниченной линиями: y=x²,y=0,x=1,x=2.

Решение.

Выполним чертеж (слайд 6). Фигура лежит в верхней полуплоскости, следовательно, функция на заданном отрезке интегрирования принимает положительные значения. Применим формулу Ньютона - Лейбница и вычислим значение определенного интеграла:

(кв. ед.)

Задача № 2. Вычислить площадь фигуры, ограниченной линиями:

.

Решение.

Выполним чертеж (слайд 7). Фигура лежит в верхней полуплоскости, следовательно, функция на заданном отрезке интегрирования принимает положительные значения. Данная фигура ограничена графиками двух функций Найдем пределы интегрирования из решения уравнения: .

Отсюда по теореме Виета имеем корни .

Т. к. верхняя часть фигуры ограничена графиком функции , то выражение для вычисления площади будет иметь вид: .

Решим данные интегралы метолом непосредственного интегрирования:

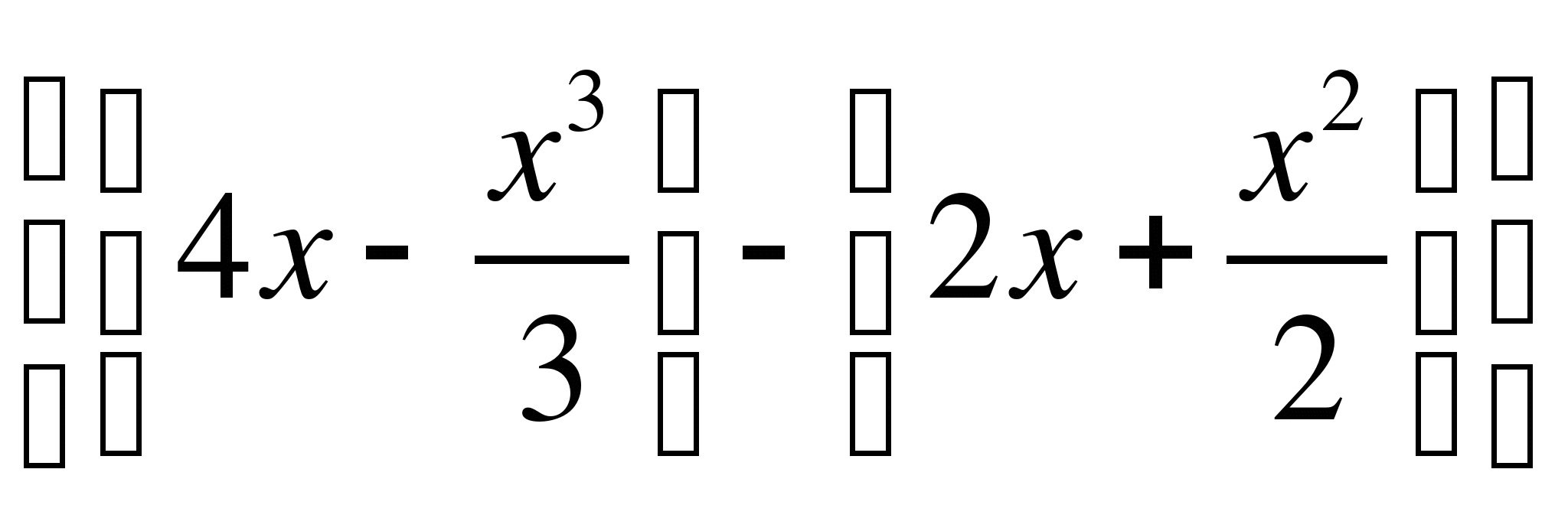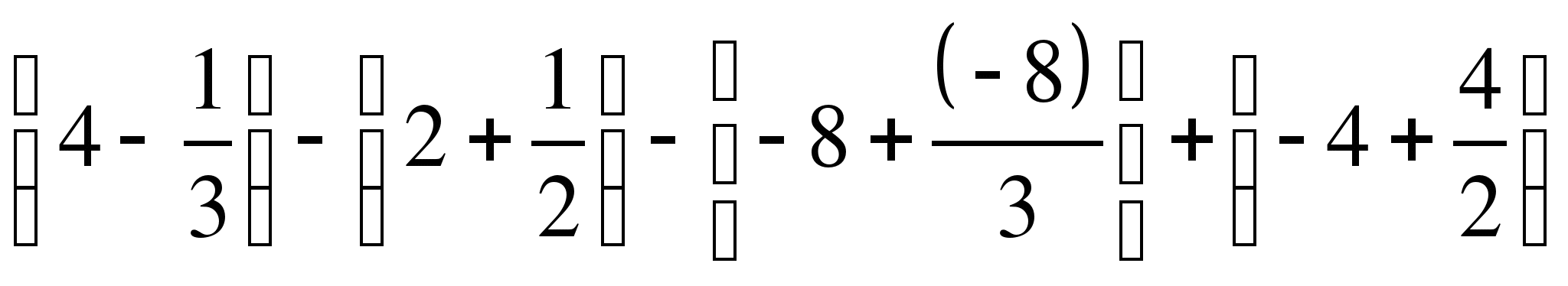= │= = 6 ++2 - = .

Проверочное задание на вычисление площади фигуры с последующей проверкой.

Проверь себя:

Вариант 1.

Не выполняя построений, вычислите площадь фигуры, ограниченной линиями: .

Вариант 2.

Не выполняя построений, вычислите площадь фигуры, ограниченной линиями: .

Проверка:

Вариант 1.

Не выполняя построений, вычислите площадь фигуры, ограниченной линиями: .

Решение.

│==.

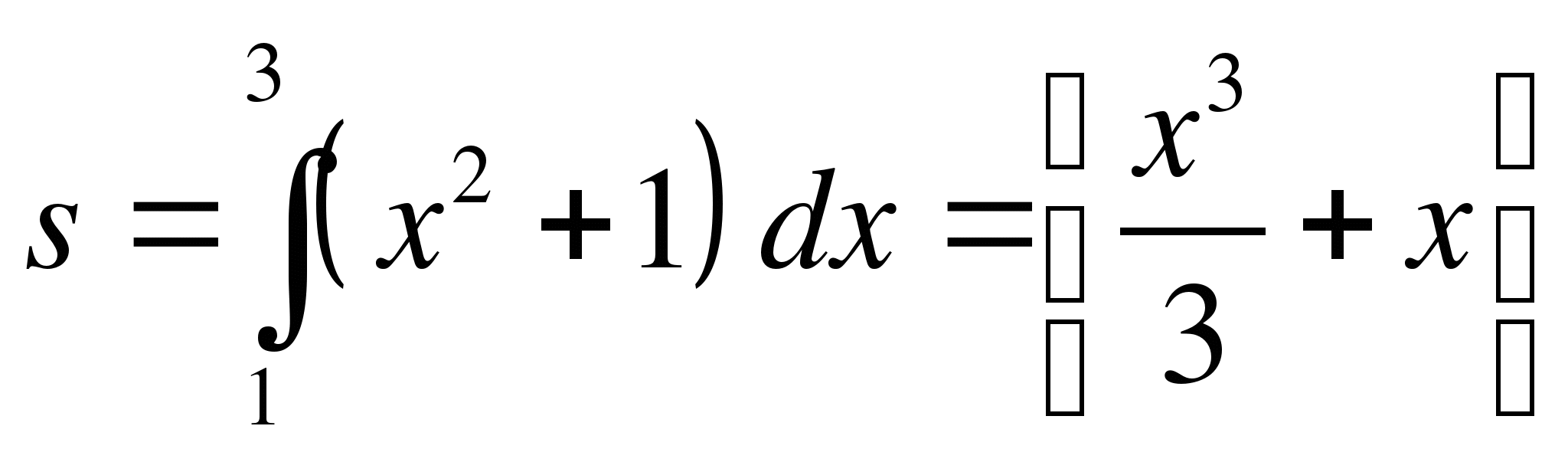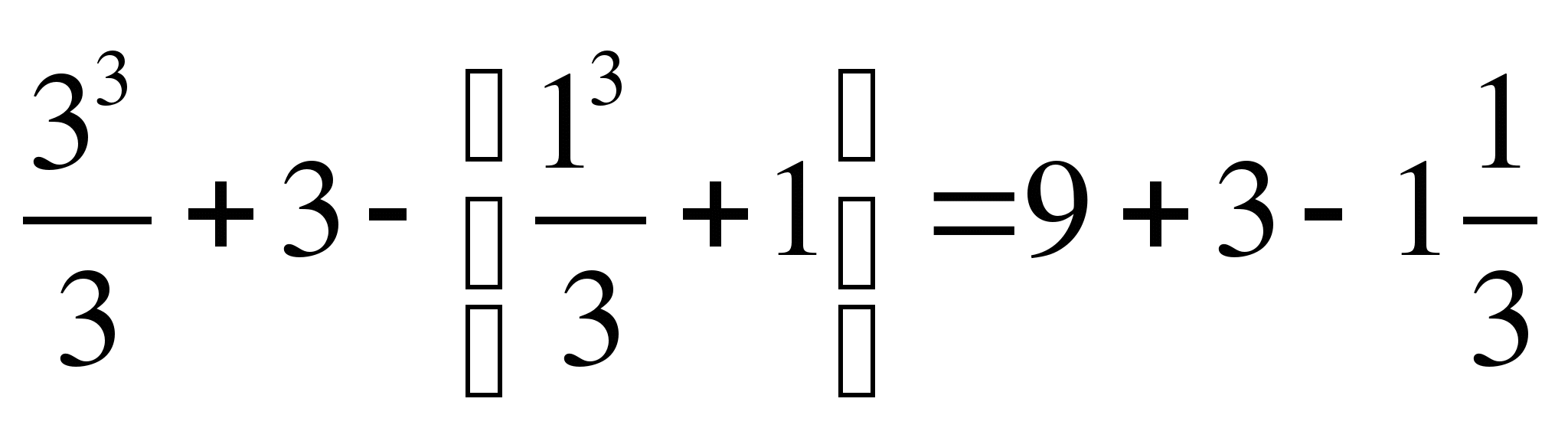Вариант 2.

Не выполняя построений, вычислите площадь фигуры, ограниченной линиями: .

Решение.

│==.

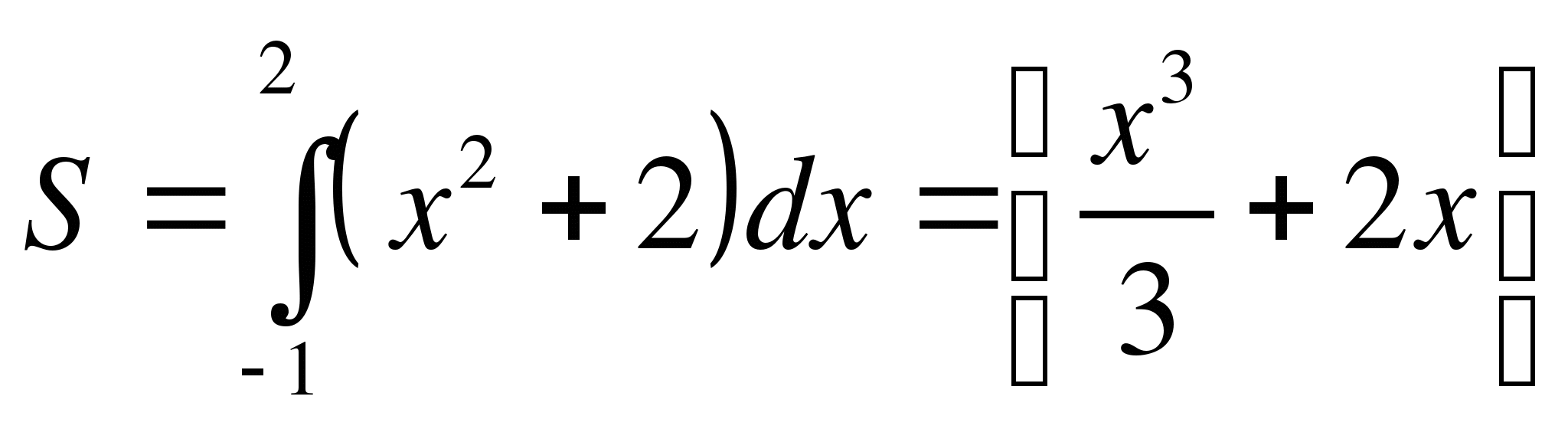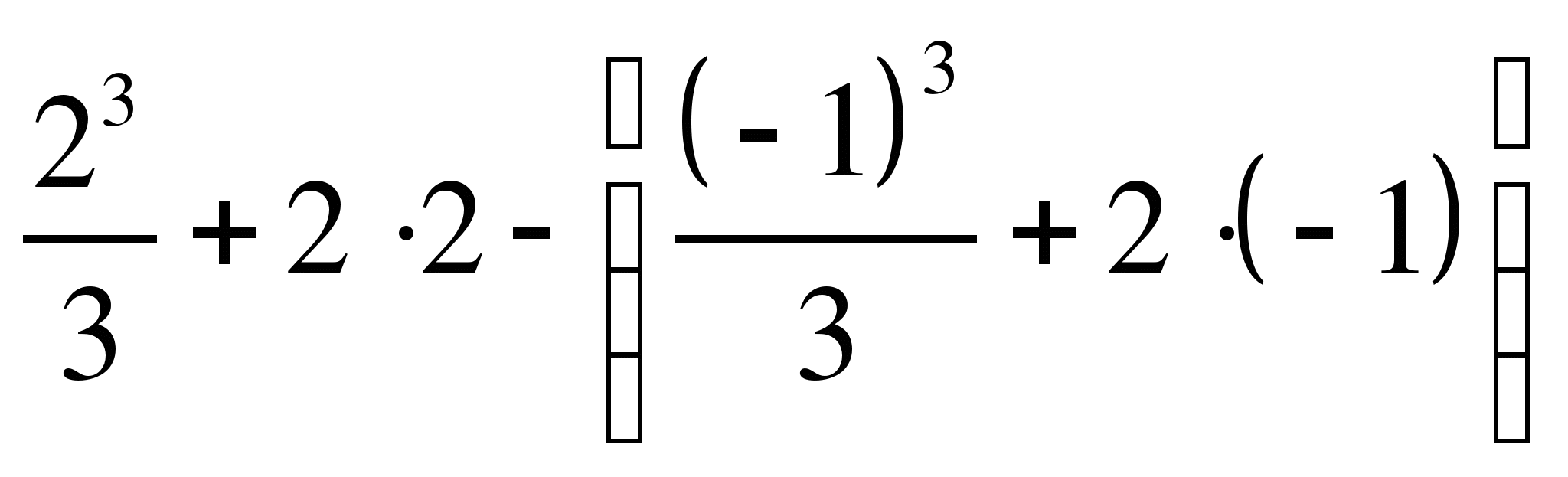2. Вычисление объемов тел вращения.

Если криволинейную трапецию вращать около одной из осей, получится геометрическое тело, называемое телом вращения.

Объем такого тела находят по формуле (слайд 9).

Задача № 3. Вычислить объем тела вращения: .

Решение.

.

Задача № 4. Вычислить объем тела вращения: .

Решение.

│=9-4=5.

Вычислить объем тела вращения:

а); б) (у доски). Как найти пределы интегрирования?

Самостоятельная работа. Найти площадь фигуры, ограниченной линиями:

1 вариант: а);

2 вариант: б)

Кроме этого с помощью определенного интеграла можно находить физические величины: путь, пройденный телом, работа переменной силы и т. д. (слайд 10, 11).

Домашнее задание: Колмогоров А. Н. №353(а, б), 354(а, б), 370(а, б).

Решение упражнений. Колмогоров А. Н. №353(в, г), 354(в, г),

Подведение итогов урока:

1. Какие величины можно вычислять с помощью определенного интеграла?

2. Как называется формула для вычисления площади фигуры, ограниченной кривой?

3. Запишите эту формулу.

4. Запишите формулу для вычисления объема.

Выставление оценок.