Конспект урока по математике для 5 класса Доли.Обыкновенные дроби

Составляющие этапа введения нового материала

Учитель

Ученики

Методические

комментарии

Актуализация знаний, умений

Изучение математики 5 класса мы начали с темы «Натуральные числа». Ребята, давайте вспомним определение натуральных чисел. ( Числа, которые… )

Устная работа . (Выполним действия с натуральными числами)

Запись на доске:

32:8 =

35 : 7 =

6 ∙ 9 =

(4 +5) ∙ 5 =

1:6= ?

-Ребята, в чем суть проблемы, с которой вы только что столкнулись?

- Вы замечали, что результат деления не всегда удается выразить натуральным числом? Приходится учитывать части и доли целого. Так появляются дробные числа.

В русском языке слово «дробь» появилось в 8 веке, оно происходит от глагола «дробить» - разбивать, ломать на части.

- Ребята, вы догадались, о чём пойдет речь на сегодняшнем уроке?

(Тема урока: «Доли. Дроби»). (Слайд №1)

-В первых учебниках математики (в XVII веке) дроби назывались «ломаные числа» Современное обозначение дробей берет свое начало в Древней Индии. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка "попасть в дроби". Ребята, что, по-вашему, означает выражение «Попасть в дроби»? (попасть в трудное положение)

- Но сегодня мы с вами на уроке докажем, что дроби не смогут нас поставить в трудное положение.

- Вы согласны со мной? Тогда давайте попробуем помочь мальчикам, которые чуть не подрались.

Дело было так:

Бабушка принесла Ване и Пете шоколадку. Мальчики заспорили:

- Моя шоколадка, - сказал Петя.

- Нет, моя! - закричал Ваня.

Назревала драка. Что в такой ситуации надо делать? (Предложите мирный выход из этой ситуации)

- Людям часто приходится делить целое на равные части. Например, торт, пирог, арбуз режут на равные куски, их называют доли. (Слайд №2)

- Самая известная доля - это, конечно, половина. Слова с приставкой "пол" вы можете услышать каждый день: полчаса, полкилограмма, полбулки.

Назовите еще несколько слов с этой приставкой.

Название доли зависит от того, на сколько равных частей разделили единицу.

Разделили на две части - "половина", на три - "треть", на четыре - "четверть", на шесть - "шестая часть", и т.д.

-Ребята, что же такое доля?

-Давайте сверим ваши ответы с правильным ответом!

( Слайд №2)

Слушают повествование учителя, отвечают на вопросы, формулируют определение.

Деление не выполняется.

Пытаются сформулировать тему урока. Записывают тему урока в тетради.

Ребята предлагают свои версии. (Попасть в трудное положение, попасть в тупик)

( - надо просто разделить шоколадку на двоих поровну, т.е. на две равные части)

Ответы детей. ( полпути, пол-лимона, полгода и т.д.)

Ответы учащихся.

Привлекаются знания и опыт учащихся, полученные ранее, поэтому задания не вызывают затруднения.

У учащихся формируется умение высказывать свои предположения и оформлять свои мысли в устной форме.

Создание проблем­ной ситуации

Ребята, перед вами на столе лежат геометрические фигуры.

- Давайте разделим наши фигуры (сгибанием) на две равные части - доли.

( у первой команды - прямоугольник, у второй - квадрат)

(Рассмотреть различные способы деления прямоугольника и квадрата на две равные части)

- А теперь разделим эти фигуры на четыре доли (рассмотреть все возможные варианты)

- Что же мы получили, разделив целое на равные части? (мы получили доли).

-Какие доли получились у нас?( половина и четверть)

- Прочитай еще раз определение: Доля - это каждая из равных частей одного целого.

-Как же записать долю с помощью математических знаков? (Слайд №3) - На экране изображен прямоугольник, который разделен на 8 частей - на 8 долей (Слайд №4), три доли выделяем цветом)Сколько долей выделено цветом - 3 , из скольких долей - из восьми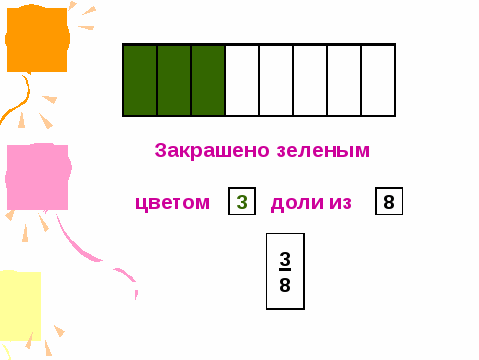

-В математике эти числа записываются в виде дроби, вот так (слайд №5)

Работают в группах, находят способы решения предложенного задания.

Делают записи в тетради.

Ребята учатся самостоятельности, стараются найти выход из затруднительного положения, учатся отстаивать свою точку зрения и творчески мыслить.

Создается проблемная ситуация с помощью вопроса, ответом на который будет новое знание.

Ведение побуждающего диалога. Формулирование учебной проблемы

- Ребята, можно ли выполнить деление чисел 1:6;1:2; 3:4; 2:5?

- Как вы считали раньше?

-Как вы считаете теперь?

Ответы учащихся.

-(Раньше мы считали, что такое деление выполнить нельзя, так как делимое меньше делителя)

- (Теперь мы знаем, что такое деление можно выполнить и результат записать в виде дроби)

Ведение побуждающего диалога позволяет ученикам выстроить логическую цепочку и ориентироваться в своей системе знаний.

Выдвижение гипотезы

Запись вида 3/8 называется обыкновенная дробь (Слайд №6).

Вопросы к классу:

-С каким новым понятие мы встретились? (обыкновенные дроби)

-Решением какого вопроса мы должны заняться сейчас?

-Ребята, внимательно посмотрите на запись вида 3/8. Что означает черта? (деление)

-Как называются элементы деления? (делимое, делитель, частное)

-Можно ли запись 3/8 назвать частным чисел 3 и 8? (Да)

-Используем ли мы числа 3и 8 при счёте? (Да)

-Как называются числа, которые мы используем при счёте? (Натуральные)

-Ребята, попробуйте сформулировать понятие « Обыкновенная дробь»

Слушают учителя, отвечают на вопросы.

-Мы должны выяснить, какие дроби называются обыкновенными.

Формулируют новое понятие:

-Частное двух натуральных чисел, где деление записывается чертой, называется обыкновенной дробью.

С помощью наводящих вопросов ученик следит за мыслью учителя и в итоге сам формулирует новое понятие.

Проверка гипотезы

-Давайте вспомним, с какой проблемой мы столкнулись в начале урока?

-Сможете ли вы теперь решить данную проблему? Сейчас мы это проверим.

Класс делится на пары. Нужно выполнить самостоятельные работы.

Вариант 1.

1. 1 разделите на 5; 7 на 15; 83 на 100. Запишите получен­ные дроби.

2. Запишите дроби: а) четыре седьмых, б) четыре шестнадцатых, в) двадцать три пятидесятых, г) шестьдесят семисотых.

3.Запишите дроби: а)с числителем 12 и знаменателем 35; б)со знаменателем 75 и числителем 23.

Вариант 2.

1. 2 разделите на 3; 9 на 14; 99 на 1000. Запишите полученные дроби.

2.Запишите дроби: а) семь одиннадцатых; б) сорок одна пятидесятая; в)семь восьмидесятых; г) пятьдесят шестисотых.

3. Запишите дроби: а)с числителем 17 и знаменателем 25; б)со знаменателем 83 и числителем 16.

Ученики формулируют проблему, которая возникла в начале урока. Выполняют самостоятельные работы, осуществляют взаимоконтроль.

Благодаря работе в парах и взаимоконтролю, ученики не только лучше усваивают материал, но и учатся работать в коллективе и развивают коммуникативность.