Урок алгебры в 7 классе «Возведение в квадрат суммы и разности двух выражений»

Схема конспекта урока

Фалькина Любовь Кузьминична, учитель математики муниципального казенного

общеобразовательного учреждения «Средняя школа № 6»

городского округа город Фролово

Предмет - алгебра

Класс - 7 «А» класс

Тема урока: «Возведение в квадрат суммы и разности двух выражений».

Тип урока: урок изучения и первичного закрепления новых знаний.

Цель: Вывести формулы квадратов суммы и разности двух выражений. Сформировать умение практически их применять.

Задачи:

• проверить знания обучающихся по теме «Произведение одночленов и многочленов»;

• познакомить с формулами сокращенного умножения;

• развивать математическое мышление, навыки творческо-поисковой деятельности, математической речи, памяти, интереса к математике;

• содействовать воспитанию активности, внимательности, самостоятельности обучающихся.

Оборудование: компьютер, проектор, экран, мультимедийная презентация, карточки «Математическое домино», карточки с тестовыми заданиями.

Содержание этапа

1.

Организационный момент

Цели и задачи: подготовить обучающихся к работе на уроке.

Метод организации: словесный

Учитель проверяет у класса подготовленность рабочего места, создает положительный настрой, объявляет цели и задачи урока, включает в учебный ритм.

2.

Опрос обучающихся по заданному на дом материалу

Цели и задачи:

установить правильность и осознанность выполнения домашнего задания обучающимися, устранить в ходе проверки обнаруженные пробелы в знаниях.

Методы: репродуктивный, объяснительный.

Проверить, закрепить знания по теме «Произведение одночленов и многочленов».

Проверка домашнего задания с помощью фронтальной беседы. Участие в поиске более полных и правильных ответов на поставленные вопросы. Создание атмосферы важности работы.

Проверка домашнего задания.

В начале урока учащимся предлагаются задания, которые с одной стороны ориентированы на повторение ранее изученного материала, а с другой стороны подводят их непосредственно к изучению нового материала.

1. Найдите квадраты выражений b; - 3; 6а; 7х² у³.

2. Найдите произведение 5b и 3с. Чему равно удвоенное произведение этих выражений?

3. Прочитайте выражения:

а) х + у в) (к + 1)² д) (а -b)²

б) с² + р² г) р - у е) с² - х²

4. А теперь мы с вами примем участие в работе лаборатории теоретиков. В ней много правил, по которым мы работаем.

У каждого из вас есть карточка - домино. У одного ученика карточка содержит слова «Старт» и «Финиш». Он задает стартовый вопрос. Он же даст и финишный ответ. Каждый из вас должен внимательно следить за ходом игры, чтобы не пропустить свой ответ. Ответив, вы должны задать свой вопрос и.т.д.

«Математическое домино»

Начинает читать вопрос ученик, которому досталась карточка со словом «старт». Затем читает второй ученик, у которого ответ на вопрос. Потом он зачитывает вопрос со своей карточки. Третий ученик, которому досталось продолжение, читает ответ, и зачитывает вопрос со своей карточки и т.д. Заканчивает игру снова первый ученик.

1. «Финиш»

Ответ: Каждый член одного многочлена умножить на каждый член другого многочлена и результаты сложить.

«Старт»

Вопрос: Что называют многочленом?

2. Ответ: Сумму одночленов.

Вопрос: Что называют одночленом?

3. Ответ: Произведение чисел, переменных и их степеней.

Вопрос: Какие слагаемые называются подобными?

4. Ответ: Слагаемые с одинаковой буквенной частью.

Вопрос: Как привести подобные слагаемые?

5. Ответ: Сложить их числовые коэффициенты, а результат умножить на общую буквенную часть.

Вопрос: Как определить степень одночлена?

5. Ответ: Найти сумму показателей степеней всех входящих в него переменных.

Вопрос: Как умножить одночлен на многочлен?

5. Ответ: Одночлен умножить на каждый член многочлена, а результаты сложить.

Вопрос: Как перемножить одночлены?

5. Ответ: Перемножить числовые коэффициенты, затем перемножить степени с одинаковыми основаниями и результаты перемножить.

Вопрос: Как умножить степени с одинаковыми основаниями?

5. Ответ: Основание оставить тем же, а показатели степеней сложить.

Вопрос: Как определить степень многочлена?

5. Ответ: Надо определить наибольшую из степеней входящих в него одночленов.

Вопрос: Как умножить многочлен на многочлен?

5. Перемножить данные многочлены:

( 4 - а) · (3 + а).

3.

Объяснение нового учебного материала.

Цели и задачи:

- формировать у обучающихся знания о формулах сокращенного умножения;

- вывести формулы квадратов суммы и разности двух выражений;

- развивать математическое мышление, навыки творческо-поисковой деятельности.

Методы: исследовательский, словесный, наглядный (компьютерная презентация).

Эпиграф нашего урока (1 слайд):

Китайская мудрость гласит,

«Я слышу - я забываю,

я вижу - я запоминаю,

я делаю - я понимаю».

Ещё в глубокой древности было подмечено, что некоторые многочлены можно умножать короче, быстрее, чем остальные. Первые общие утверждения о тождественных преобразованиях встречаются у древнегреческих математиков, начиная с VI века до н.э. Среди математиков Древней Греции было принято выражать все алгебраические утверждения в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, произведение двух чисел истолковывали как площадь прямоугольника. Отказ от геометрической трактовки наметился у Диофанта Александрийского, жившего в III веке. В его работах появляются зачатки буквенной символики и специальных обозначений. Формулы квадрата суммы и разности двух выражений знали еще в Древнем Вавилоне, а древнегреческие математики знали ее геометрическое истолкование.

Так появились формулы сокращённого умножения. Их несколько. Сегодня вам предстоит сыграть роль исследователей и «открыть» две из этих формул.

(2 слайд)

Итак, тема нашего урока - «Возведение в квадрат суммы и разности двух выражений».

А как вы думаете, для чего нужны формулы?

Правильно, они упрощают вычисления.

Еще с помощью формул, которые вы выведете, можно возводить большие числа в квадрат и довольно быстро.

(Для исследовательской работы учащиеся объединяются в 3 группы. В них входят ребята с разной математической подготовкой. Каждой группе предлагается заполнить на доске две строки таблицы, перемножив пары двучленов, приведённых в этой строке. После того как ребята справились с заданиями, один из них выходит к доске и записывает в правом столбце таблицы полученный ответ. Средняя часть таблицы закрыта.)

Задание: Найти произведение данных многочленов

Вопросы: 1) Есть ли нечто общее в условиях и ответах?

2) Можно ли выражения в I столбце записать короче?

( Получив ответы, учитель открывает II столбец.)

Вы уже приступили к исследованию темы урока, поскольку находили произведение двух одинаковых двучленов (1 столбец таблицы), т.е. возводили в квадрат сумму или разность двух выражений (2 столбец таблицы).

Обсуждение полученных результатов

Анализ III столбца:

1. После приведения подобных членов подсчитайте, сколько получилось членов в каждом многочлене? (ответ: трёхчлен)

2. Что представляет собой 1-й, 2-й и 3-й члены по сравнению с 1-м и 2-м выражениями, стоящими в основании соответствующей степени?

1-й член - квадрат первого выражения.

2-й член - удвоенное произведение первого и второго выражений.

3-й член - квадрат второго выражения.

Итог. (3 слайд)

Учащиеся записывают общую формулу квадрата суммы двух выражений и дают словесное описание:

- формула сокращённого умножения.

(подчёркивается, что эта формула в дальнейшем будет применяться для возведения в квадрат суммы двух выражений).

Изменяется ли результат, если возвести в квадрат не , а

Сравнивая результаты из таблицы, учащиеся выясняют, что «минус» стоит только перед удвоенным произведением.

(4 слайд)

.

(Формулы записываются в тетрадь.)

Физкультминутка:

Выполнить наклоны в стороны, потянуться вверх, зарядка для глаз.

Геометрическая интерпретация формул сокращенного умножения :

А) (5 слайд) геометрическое истолкование формулы .

Объясните геометрический смысл формулы? (Площадь квадрата со стороной a+b равна сумме площадей квадрата со стороной а, двух площадей прямоугольника со сторонами а и в и площади квадрата со стороной в).

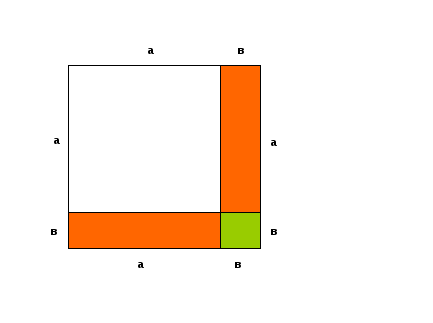
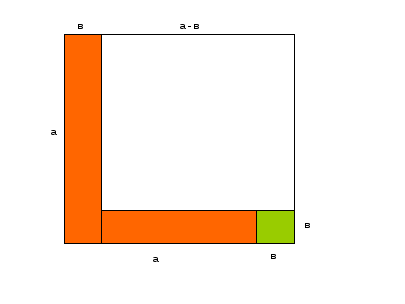
Б) (6 слайд) геометрическое истолкование формулы .

Объясните геометрический смысл формулы? (Площадь квадрата со стороной a-b равна площади квадрата со стороной а без удвоенной площади прямоугольника со сторонами а и в и добавочной площади квадрата со стороной в).

4.

Закрепление учебного материала

Цели и задачи:

сформировать умение применять полученные формулы на практике.

Методы:

- фронтальная работа;

- работа в группах.

1. Первичное закрепление. Работа у доски по учебнику - № 799 (г, ж) (Алгебра. 7 класс: учебник для общеобразовательных учреждений / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова; под ред. С.А.Теляковского. - 19-е изд. - М.: Просвещение, 2010).

2. Групповая работа. Каждая группа работает самостоятельно, получив тестовое задание.

Выбрать правильный ответ.

А

Б

В

1) (с + 11)²

c² + 11c +121

c² - 22c + 121

c² +22c + 121

2) (7y + 6)²

49y² + 42y + 36

49y² + 84y + 36

49y² - 84y +36

3) (9 - 8y)²

81 - 144y + 64y²

81 - 72y + 64y²

81 + 144y + 64y²

4) (2x - 3y)²

4x² -12xy + 9y²

81 - 72y + 64y²

4x² - 6xy + 9y²

Результаты работы с тестами учащиеся проверяют по таблице ответов (7 слайд).

2

3

4

В

Б

А

А

Учитель оказывает консультации тем обучающимся, у которых возникают вопросы при выполнении заданий.

Если остается время, игра «Кубик - экзаменатор».

(На каждой грани записан квадрат суммы или разности двух выражений. Вызванный по желанию ученик, подбрасывает кубик и комментирует выпавшую ему на верхней грани часть формулы, называет многочлен, в который можно преобразовать данный квадрат двучлена).

(4zy - 3р)²

(b - 3)²

(g + 5c)²

(4c²- 5t)²

(1/2x + 1)²

(7c + 5p)²

5.

Подведение итогов. Рефлексия.

Цели и задачи:

осознание того, что усвоено и что еще нужно усвоить.

Методы: наглядный, словесный.

Как вы считаете, вы справились с исследовательской деятельностью? Кто может сказать, какие формулы вы сегодня вывели? Как звучит правило? Все ли было понятно?

Оценки за урок.

5.

Задание на дом

Цели и задачи:

учить школьников самоорганизации при выполнении учебной задачи.

Метод: словесный.

Учитель комментирует домашнее задание:

- что должны сделать обучающиеся в ходе выполнения домашнего задания;

- определение целей, которых хочет достичь учитель, задавая задание на дом;

- определение и разъяснение учащимся критериев успешного выполнения домашнего задания.

Домашнее задание носит дифференцированный характер (8 слайд).

П.32 (стр. 153 - 154);

I группа: № № 799 (д, з, и, к); 800;

II группа: №№ 803; 804.

(9 слайд) СПАСИБО ЗА УРОК.