- Учителю
- Тест по теме Углы и отрезки, связанные с окружностью. Решение треугольников, 10 класс
Тест по теме Углы и отрезки, связанные с окружностью. Решение треугольников, 10 класс
Тест по теме «Углы и отрезки, связанные с окружностью.
Решение треугольников»
10 класс
(к п.85-93 учебника Геометрия,10-11, Л.С. Атанасян)
Вариант 1.
-
Произведение отрезков одной из двух пересекающихся хорд равно
-
Квадрату суммы отрезков другой хорды;
-
Произведению отрезков другой хорды
-
Длине другой хорды.
-
-
Квадрат касательной равен
-
Произведению секущей на ее внешнюю часть;
-
Произведению отрезка секущей, заключенного внутри окружности, на ее внешнюю часть;
-
Произведению секущей на отрезок секущей, заключенный внутри окружности.
-
-
Угол между двумя пересекающимися хордами измеряется
-
Полуразностью заключенных между ними дуг
-
Половиной произведения заключенных между ними дуг
-
Полусуммой заключенных между ними дуг.
-
-
Угол между двумя секущими, проведенными из одной точки, измеряется
-
Полуразностью заключенных между ними дуг;
-
Половиной произведения заключенных между ними дуг;
-
Полусуммой заключенных между ними дуг.
-
-
Угол между касательной и хордой, проходящей через точку касания, измеряется
-
Дугой, на которую он опирается;
-
Половиной заключенной в нем дуги;
-
Полуразностью заключенных между ними дуг.
-
-
Угол между касательной и секущей, проведенными из одной точки,
-
Равен 180 минус величина заключенной внутри него дуги большей полуокружности;
-
измеряется полуразностью заключенных внутри него дуг;
-
Равен 180 минус величина заключенной внутри него дуги меньшей полуокружности.
-
-
В любом вписанном четырехугольнике
-
Суммы противоположных сторон равны;
-
Суммы односторонних углов равны 180;
-
Суммы противоположных углов равны 180.
-
-
В выпуклый четырехугольник можно вписать окружность, если
-
Суммы противоположных сторон равны;
-
Суммы односторонних углов равны 180;
-
Суммы противоположных углов равны 180.
-
-
Угол между двумя касательными, проеденными из одной точки,
-
Равен 180 минус величина заключенной внутри него дуги большей полуокружности;
-
измеряется полуразностью заключенных внутри него дуг;
-
Равен 180 минус величина заключенной внутри него дуги меньшей полуокружности.
-
-
Из теоремы о квадрате медианы треугольника можно вывести формулу медианы треугольника:
-
ma= ;
-
mc= ;
-
mb= .
-
-
Сумма квадратов диагоналей параллелограмма равна
-
Сумме квадратов его сторон;
-
Полусумме квадратов его сторон;
-
Половине произведения его смежных сторон.
-
-
Теорема синусов выражается формулой
-
Биссектриса треугольника делит его сторону на части
-
Пропорциональные двум другим сторонам;
-
Пропорциональные двум другим биссектрисам;
-
Пропорциональные квадратам двух других сторон.
-
-
Теорема косинусов выражается формулой
-
cosС=
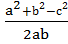 .
.
-
Запишите формулы для нахождения площади треугольника: произвольного (через сторону и высоту), прямоугольного, равностороннего, формулу Герона, через синусы углов треугольника, через 2 стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности.
Тест по теме «Некоторые сведения из планиметрии»
10 класс
Вариант 2.
-
Угол между касательной и хордой, проходящей через точку касания, измеряется
-
Дугой, на которую он опирается;
-
Половиной заключенной в нем дуги;
-
Полуразностью заключенных между ними дуг.
-
-
Сумма квадратов диагоналей параллелограмма равна
-
Сумме квадратов его сторон;
-
Полусумме квадратов его сторон;
-
Половине произведения его смежных сторон.
-
-
Квадрат касательной равен
-
Произведению секущей на ее внешнюю часть;
-
Произведению отрезка секущей, заключенного внутри окружности, на ее внешнюю часть;
-
Произведению секущей на отрезок секущей, заключенный внутри окружности.
-
-
Угол между двумя секущими, проведенными из одной точки измеряется
-
Полуразностью заключенных между ними дуг;
-
Половиной произведения заключенных между ними дуг;
-
Полусуммой заключенных между ними дуг.
-
-
Произведение отрезков одной из двух пересекающихся хорд равно
-
Квадрату суммы отрезков другой хорды;
-
Произведению отрезков другой хорды
-
Длине другой хорды.
-
-
Угол между касательной и секущей, проведенными из одной точки,
-
Равен 180 минус величина заключенной внутри него дуги большей полуокружности;
-
измеряется полуразностью заключенных внутри него дуг;
-
Равен 180 минус величина заключенной внутри него дуги меньшей полуокружности.
-
-
Теорема косинусов выражается формулой
-
cosС=
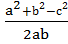 .
.
-
Угол между двумя пересекающимися хордами измеряется
-
Полуразностью заключенных между ними дуг
-
Половиной произведения заключенных между ними дуг
-
Полусуммой заключенных между ними дуг.
-
-
Угол между двумя касательными, проеденными из одной точки,
-
Равен 180 минус величина заключенной внутри него дуги большей полуокружности;
-
измеряется полуразностью заключенных внутри него дуг;
-
Равен 180 минус величина заключенной внутри него дуги меньшей полуокружности.
-
-
В выпуклый четырехугольник можно вписать окружность, если
-
Суммы противоположных сторон равны;
-
Суммы односторонних углов равны 180;
-
Суммы противоположных углов равны 180.
-
-
Из теоремы о квадрате медианы треугольника можно вывести формулу медианы треугольника:
-
ma= ;
-
mc= ;
-
mb= .
-
-
Биссектриса треугольника делит его сторону на части
-
Пропорциональные двум другим сторонам;
-
Пропорциональные двум другим биссектрисам;
-
Пропорциональные квадратам двух других сторон.
-
-
Теорема синусов выражается формулой
-
В любом вписанном четырехугольнике
-
Суммы противоположных сторон равны;
-
Суммы односторонних углов равны 180;
-
Суммы противоположных углов равны 180.
-
-
Запишите формулы для нахождения площади треугольника: произвольного (через сторону и высоту), прямоугольного, равностороннего, формулу Герона, через синусы углов треугольника, через 2 стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности.
</
Ответы на тест
-
п/п
Вариант 1
Вариант 2
B
B
A
A
C
А
A
A
B
B
B
В
C
А
A
С
C
С
A
А
A
А
B
А
A
В
A
С
S=
 а, S=
а, S= ab,
, S =
ab,
, S =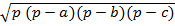 ,
, S=
,
, S= ab,
S =
ab,
S =  Р r,
Р r,