Рабочая программа по математике 9 класс к учебнику Мордкович

Учебно-тематическое планирование по математике

Класс - 9

Учитель - Фатыхова Елена Васильевна

Количество часов - 170

Всего 170 час; в неделю 5 час.

Плановых контрольных уроков 12, из них 5 по геометрии, 7 по алгебре, в том числе 1 итоговая контрольная работа,

Планирование составлено на основе программы для общеобразовательных учреждений: Математика. 5-11 классы Алгебра 7-9- классы. Алгебра и начала математического анализа. 10-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. - М.: Мнемозина, 2007, рекомендованная Департаментом образовательных программ и стандартов общего образования МО РФ

Учебник

1. Алгебра, учебник для 9 класса общеобразовательных учреждений / А.Г. Мордкович 2012

2. Алгебра, задачник для 9 класса общеобразовательных учреждений / А.Г. Мордкович 2012

3. Геометрия, 7 - 9. Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.: Просвещение, 2005.

Источники информации и средства обучения

1. Алгебра, учебник для 9 класса общеобразовательных учреждений / А.Г. Мордкович 2012

2. Алгебра, задачник для 9 класса общеобразовательных учреждений / А.Г. Мордкович 2012

3. Геометрия, 7 - 9. Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.: Просвещение, 2005.

4. Алгебра 7 - 9. Методическое пособие для учителя. / Мордкович А.Г.

5. Изучение геометрии в 7 - 9 классах. Методические рекомендации к учебнику. Книга для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков: Просвещение, 2004.

6. Алгебра, 9 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л.А. Александрова: Мнемозина, 2009.

7. Алгебра, 9 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л.А. Александрова: Мнемозина, 2009.

8. Дидактические материалы по геометрии для 9 класса / Б.Г. Зив, В.М. Мейлер: Просвещение, 2004.

9. Самостоятельные и контрольные работы по алгебре и геометрии для 9 класса / А.П. Ершова, В.В. Голобородько, А.С. Ершов: Илекса, 2004.

10. Задачи и упражнения на готовых чертежах. 7 - 9 классы. Геометрия / Е.М. Рабинович: Илекса, 2001.

Пояснительная записка

Материалы для рабочей программы для 9 класса составлены на основе:

• федерального компонента государственного стандарта общего образования,

• примерной программы по математике основного общего образования,

• федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях,

Согласно федеральному базисному учебному плану на изучение математики в 9 классе отводится не менее 170 часов из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии может быть следующим:

- 3 часа в неделю алгебры и 2 часа в неделю геометрии в течение всего учебного года, итого 102 часа алгебры и 68 часов геометрии.

Обучение математике в основной школе направлено на достижение следующих целей:

1) в направлении личностного развития:

• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и математических способностей;

2) в метапредметном направлении:

• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении:

• овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;

• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

Общая характеристика учебного предмета

Курс математики 9 класса включает следующие разделы: алгебра, функции, вероятность и статистика, геометрия, которые изучаются блоками. В соответствии с этим составлено тематическое планирование.

Содержание раздела «Алгебра» направлено на формирование у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. В задачи изучения алгебры входят также развитие алгоритмического мышления и овладение навыками дедуктивных рассуждений.

Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов.

Раздел «Вероятность и статистика» - обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим для формирования у учащихся умений воспринимать и критически оценивать информацию, представленную в различных формах.

Цель содержания раздела «Геометрия» - развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур и применение этих свойств при решении задач вычислительного и конструктивного характера.

Два дополнительных разделы «Логика и множества» и «Математика в историческом развитии» изучаются в ходе рассмотрения различных вопросов курса. Раздел «Логика и множества» - служит цели овладения учащимися некоторыми элементами ниверсального математического языка, раздел «Математика в историческом развитии» - способствует созданию общекультурного, гуманитарного фона изучения курса.

Требования к уровню подготовки обучающихся

В результате изучения математики ученик должен:

Знать:

• Существо понятия математического доказательства; примеры доказательств;

• Существо понятия алгоритма; примеры алгоритмов;

• Как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• Как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• Как потребности практики привели математическую науку к необходимости расширения понятия числа;

• Вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• Каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• Смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

Арифметика

Уметь:

• Выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;

• Переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;

• Выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;

• Округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и избытком, выполнять оценку числовых выражений;

• Пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;

• Решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• Решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных материалов, калькулятора, компьютера;

• Устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;

• Интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;

Алгебра

Уметь:

• Составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• Выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• Применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;

• Решать линейные и квадратные неравенства с одной переменной и их системы;

• Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• Изображать числа точками на координатной прямой;

• Определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;

• Распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;

• Находить значения функции, заданной формулой, таблицей, графиком, по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• Определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

• Описывать свойства изученных функций, строить их графики;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• Выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• Моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

• Описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• Интерпретации графиков реальных зависимостей между величинами;

Элементы логики, комбинаторики, статистики и теории вероятностей

Уметь:

• Проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и примеры для опровержения утверждений;

• Извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

• Решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;

• Вычислять средние значения результатов измерений;

• Находить частоту события, используя собственные наблюдения и готовые статистические данные;

• Находить вероятности случайных событий в простейших случаях;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• Выстраивания аргументации при доказательстве (в форме монолога и диалога);

• Распознавания логически некорректных рассуждений;

• Записи математических утверждений, доказательств;

• Анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• Решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• Решения учебных и практических задач, требующих систематического перебора вариантов;

• Сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;

• Понимания модели с реальной ситуацией;

• Понимания статистических утверждений.

Геометрия

знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

уметь

• пользоваться языком геометрии для описания предметов окружающего мира;

• распознавать геометрические фигуры, различать их взаимное расположение;

• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;

• распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;

• в простейших случаях строить сечения и развертки пространственных тел;

• проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;

• вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;

• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

• решать простейшие планиметрические задачи в пространстве;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• описания реальных ситуаций на языке геометрии;

• расчетов, включающих простейшие тригонометрические формулы;

• решения геометрических задач с использованием тригонометрии;

• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

построений геометрическими инструментами (линейка, угольник, циркуль, транспортир

Место учебного предмета в учебном плане школы

Согласно учебному плану МБОУ «Чепчуговская СОШ» на 2016-2017 учебный год на изучение предмета «Математика» выделяется в 9 классе 170 часов (5 ч в неделю). Форма промежуточной аттестации - контрольные работы

Содержание образовательной программы

1). Рациональные неравенства (12 ч).

Решение рациональных неравенств методом интервалов. Решение систем рациональных неравенств.

Основная цель - сформировать умение решать неравенства и системы неравенств и научить использовать полученные навыки их решения при исследовании корней квадратных уравнений, содержащих параметр.

2). Системы уравнений (19 ч).

Уравнение с двумя переменными, его решение и график. Системы рациональных уравнений, основные методы их решения: графический, подстановка, алгебраическое сложение, введение новых переменных. Понятие о равносильности систем уравнений. Системы уравнений как математические модели реальных ситуаций (текстовые задачи).

Основная цель - научить учащихся решать системы уравнений с двумя переменными различными способами и использовать полученные навыки при решении задач.

3). Числовые функции (24 ч).

Определение функции, способы задания функции. Область определения, область значений функции. Свойства функций: монотонность, ограниченность, наибольшее и наименьшее значения функции на заданном промежутке. Четные и нечетные функции, особенности их графиков. Наглядно-геометрические представления о непрерывности и выпуклости

Основная цель - выработать умение исследовать функции по заданному графику. При изучении материала данной главы функциональные представления учащихся существенно расширяются и углубляются.

4). Прогрессии (16 ч).

Определение числовой последовательности и способы ее задания: аналитический, словесный, рекуррентный. Монотонные последовательности. Арифметическая и геометрическая прогрессии: определения, формулы л-го члена, формулы суммы п членов, характеристические свойства.

Основная цель - познакомить учащихся с понятиями арифметической и геометрической прогрессий.

5). Элементы комбинаторики, статистики и теории вероятностей. (12 ч).

Основная цель - сформировать умение воспринимать и анализировать информацию, представленную в различных формах, понимание вероятностного характера многих реальных зависимостей, научить производить простейшие вероятностные расчеты.

6). Итоговое повторение (19 ч).

Основная цель - подготовить учащихся к итоговой аттестации.

Векторы. Метод координат.

Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.

Цель: научить обучающихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач.

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов.

Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах.

Цель: развить умение обучающихся применять тригонометрический аппарат при решении геометрических задач.

Длина окружности и площадь круга.

Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.

Цель: расширить знание обучающихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления.

Движения.

Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения.

Цель: познакомить обучающихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений.

Об аксиомах геометрии.

Беседа об аксиомах геометрии.

Цель: дать более глубокое представление о системе аксиом планиметрии и аксиоматическом методе.

В данной теме рассказывается о различных системах аксиом геометрии, в частности о различных способах введения понятия равенства фигур.

Повторение. Решение задач.

Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 9 класса.

Календарно-тематическое планирование по математике для 9 класса28.09

Пересечение и объединение множеств

29.09

Разложение вектора по двум неколлинеарным векторам

30.09

Системы неравенств

1.10

Метод координат - 11 часов

Системы рациональных неравенств

3.10

Координаты вектора

5.10

Решение задач по теме «Системы неравенств»

6.10

Связь между координатами вектора и координатами его начала и конца

7.10

Системы неравенств

8.10

Контрольная работа №2 по теме «Неравенства и системы неравенств»

10.10

Координаты середины отрезка. Вычисление длины вектора по его координатам

12.10

Обобщение и систематизация по теме «Неравенства и системы неравенств»

13.10

Системы уравнений - 16 часов

Расстояние между двумя точками

14.10

Основные понятия. Рациональные уравнения с двумя переменными

15.10

График уравнения с двумя переменными

17.10

Уравнение линии на плоскости

19.10

Формула расстояния между двумя точками координатной плоскости. График уравнения (x - a)² + (y - b)² =r²

20.10

Уравнение окружности

21.10

Системы уравнений с двумя переменными

22.10

Неравенства и системы неравенств с двумя переменными

24.10

Уравнение прямой

26.10

Метод подстановки

27.10

Составление уравнений окружности и прямой

28.10

Метод алгебраического сложения

29.10

Метод введения новых переменных

7.11

Использование уравнений окружности и прямой при решении задач

9.11

Методы решения систем уравнений

10.11

Контрольная работа №3 по теме: «Метод координат»

11.11

Системы уравнений как математические модели реальных ситуаций.

12.11

Решение текстовых задач

14.11

Соотношение между сторонами и углами треугольника. Скалярное произведение векторов - 14 часов.

Синус, косинус, тангенс угла

16.11

Решение задач на движение

17.11

Основное тригонометрическое тождество

18.11

Решение задач на движение по воде

19.11

Решение задач на работу

21.11

Формулы приведения

23.11

Контрольная работа №4 по теме «Системы уравнений»

24.11

Формулы для вычисления координат точки

25.11

Обобщение и систематизация по теме «Системы уравнений»

26.11

Системы двух линейных уравнений с двумя переменными - 26 часов

Определение числовой функции

28.11

Теорема о площади треугольника

30.11

Область определения

1.12

Теорема синусов

2.12

Область значений функции

3.12

Нахождение области определения и области значений функции

5.12

Теорема косинусов

7.12

Способы задания функции

8.12

Решение треугольников по двум сторонам и углу между ними.

9.12

Графический способ задания функции

10.12

Свойства функции.

12.12

Решение треугольника по трем сторонам

14.12

Линейная функция y= kx + m (k 0).

15.12

Угол между векторами. Скалярное произведение векторов

16.12

Функция y=kx². (k¹ 0), y=k/x.

17.12

Функция y=ax² + bx + c, y=√x.

19.12

Скалярное произведение в координатах. Свойства скалярного произведения векторов

21.12

Четные и нечетные функции

22.12

Применение скалярного произведения векторов к решению задач

23.12

Исследование функций на четность и нечётность

24.12

Подготовка к контрольной работе

9.01

Контрольная работа №5 по теме: «Соотношение между сторонами и углами треугольника»

11.01

Контрольная работа № 6 по теме « Функции»

12.01

Обобщение и систематизация знаний по теме: «Соотношение между сторонами и углами треугольника

13.01

Степенная функция с натуральным показателем

14.01

Степенная функция с чётным натуральным показателем

16.01

Длина окружности и площадь круга - 11 часов

Правильный многоугольник

18.01

Степенная функция с нечётным натуральным показателем

19.01

Окружность, описанная около правильного многоугольника

20.01

Степенная функция с натуральным показателем

21.01

Функции y= x^-n, nÎ N, их свойства и графики

23.01

Окружность, вписанная в правильный многоугольник

25.01

Степенная функция с отрицательным целым показателем

26.01

Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности

27.01

Решение задач по теме «Функции y= x^-n, nÎ N, их свойства и графики»

28.01

Кубический корень из числа

30.01

Построение правильных многоугольников

1.02

Функция y=, ее свойства и график

2.02

Длина окружности

3.02

Построение графика функции y=,

4.02

Контрольная работа №7 по теме «Степенные функции и их графики»

6.02

Площадь круга

8.02

Обобщение и систематизация по теме «Системы двух линейных уравнений с двумя переменными»

9.02

Прогрессии - 17 часов

Площадь кругового сектора

10.02

Определение числовой последовательности.

11.02

Аналитическое задание последовательности.

13.02

Вычисление длины дуги окружности и площади круга

15.02

Рекуррентное задание последовательности

16.02

Контрольная работа №8 по теме: «Длина окружности. Площадь круга»

17.02

Монотонные последовательности

18.02

Арифметическая прогрессия. Основные понятия.

20.02

Обобщение и систематизация знаний по теме: «Длина окружности. Площадь круга»

22.02

Отображение плоскости на себя

24.02

Формула n - го члена арифметической прогрессии.

25.02

Формула суммы членов конечной арифметической прогрессии

27.02

Движение - 8 часов

Понятие движения

1.03

Вычисление суммы арифметической прогрессии

2.03

Наложения и движения

3.03

Характеристическое свойство арифметической прогрессии

4.03

Геометрическая прогрессия. Основные понятия.

6.03

Формула n - го члена геометрической прогрессии

9.03

Параллельный перенос

10.03

Вычисление n - го члена геометрической прогрессии

11.03

Формула суммы членов конечной геометрической прогрессии

13.03

Поворот

15.03

Характеристическое свойство геометрической прогрессии

16.03

Решение задач по теме «Движение»

17.03

Прогрессии и банковские расчеты

18.03

Контрольная работа №10 по теме «Движение»

29.03

Контрольная работа №9 по теме «Прогрессии»

30.03

Обобщение и систематизация знаний по теме: «Движение»

31.03

Обобщение и систематизация по теме «Прогрессии»

1.04

Элементы комбинаторики, статистики и теории вероятностей - 13 часов

Комбинаторные задачи

3.04

Предмет стереометрии. Многогранники

5.04

Начальные сведения из стереометрии - 8 часов

Факториал. Перестановки.

6.04

Призма. Параллелепипед

7.04

Сочетания.

8.04

Статистика - дизайн информации

10.04

Объем тела

12.04

Группировка информации. Табличное представление информации

13.04

Свойства прямоугольного параллелепипеда

14.04

Графическое представление информации. Числовые характеристики данных измерения.

15.04

Простейшие вероятностные задачи

17.04

Пирамида Цилиндр Конус

19.04

Решение простейших вероятностных задач

20.04

Сфера. Шар

21.04

Решение вероятностных задач

22.04

Экспериментальные данные

24.04

Аксиомы планиметрии

26.04

Вероятности событий

27.04

Некоторые сведения из истории

28.04

Контрольная работа №11 по теме «Комбинаторика»

29.04

Обобщение и систематизация по теме «Комбинаторика»

3.05

Повторение курса алгебры 9 класса - 12 часов

Линейные и квадратные неравенства

5.05

Повторение курса геометрии 9 класса - 8 часов

Решение задач по теме «Координаты вектора»

6.05

Рациональные неравенства

8.05

Решение задач по теме «Метод координат»

10.05

Системы неравенств

11.05

Методы решений систем уравнений

12.05

Решение задач по теме «Решение треугольников»

13.05

Системы уравнений как математические модели реальных ситуаций

15.05

Решение задач по теме «Решение треугольников»

17.05

Числовые функции

18.05

Графики числовых функций

19.05

Решение задач по теме «Длина окружности и площадь круга»

20.05

Арифметическая прогрессия

22.05

Решение задач по теме «Движения»

24.05

Геометрическая прогрессия

25.05

Итоговая контрольная работа по математике 9 класс

Работа над ошибками

Итоговое повторение по курсу алгебра 9 класс

Обобщающий урок по курсу математики 9 класса

Итоговый урок

Заключительный урок.

Приложение 1

Критерии оценок по математике

Оценка устных ответов учащихся

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником, изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теоретические положения конкретными приме-рами, применять их в новой ситуации при выполнении практического задания;

• продемонстрировал усвоение ранее изученных сопутствующих вопросов, сфор-мированность и устойчивость используемых при отработке умений и навыков;

• отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если

• он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

• допущены один - два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.

Отметка «3» ставится в следующих случаях:

• неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);

• имелись затруднения или допущены ошибки в определении понятий, использо-вании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

• ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Оценка письменных работ учащихся

Отметка «5» ставится, если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что учащийся не владеет

обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Приложение 2

Контроль знаний учащихся 9 класса по четвертям за учебный годКонтрольная работа по математике 9класса за 1 четверть по учебнику А-9, автора А.Г.Мордкович.

Время выполнения: 1 урок.

Вариант1.

1.Решить неравенство: 12х+7≥9х-11.Ответы: 1.(-∞;-6) 2.[-6;+∞) 3.(-6;+∞) 4.(-∞;-6].

2.Решить неравенство: -2х²+9х-7<0. Ответы: 1.(1;3,5) 2.(-∞;2)ᵁ(7;+∞) 3. (2;7) 4. (-∞;1)ᵁ(3,5;+∞).

3.Найти область определения функции у= √ х²-9 . Ответы: 1.[-3;-1)ᵁ[3;+∞) 2.[-3;-1)ᵁ(-1;3] 4. (-∞;-3]ᵁ(-1;3].

4. При каких х имеет смысл выражение: √ 96-16х + √ 5х-10. Ответы: 1.[2;6] 2. (-∞; 6] 3. [2; +∞) 4.(-∞;+∞).

5.Сколько целых чисел принадлежит решению неравенства │х+3│<2.

6.Укажите длину промежутка, который является решением неравенства : -5≤ 2х+11≤1.

7. При каких значениях а уравнение: х²+(а-2)х-(а-5)=0 имеет 2 корня?

Вариант2.

1.Решить неравенство: 9х-4< 10х+3. Ответы: 1.(-∞;-7] 2. [-7;+∞) 3.(-7;+∞) 4. (-∞;7]

2. Решить неравенство: 7х²-9х+2≤0. Ответы: 1.(-∞;2/7]ᵁ[1;+∞) 2. [2/7;1] 3. (-∞;4/7]ᵁ[2;+∞) 4. [4/7;2].

3. Найти область определения функции у= √ 16-х² Ответы: 1. [-4;3)ᵁ(3;4] 2. (-∞;-4]ᵁ(3;4]

х-3 3.[-4;3)ᵁ[4;+∞) 4. (-∞;-4]ᵁ[4;+∞).

4. . При каких х имеет смысл выражение: √14х-70+ √3х-9. Ответы: 1.(-∞;3] 2.[3;5] 3.[5;+∞) 4. (-∞;+∞).

5. Сколько целых чисел принадлежит решению неравенства: │х-2│<3.

6.Укажите длину промежутка, который является решением неравенства : -3≤4х-9≤3.

7. При каких значениях а уравнение: х²-(а+1)х-(а-2)=0 не имеет корней?

Контрольная работа за 1 полугодие 9 класса

Вариант 1

1. Решить неравенство 2х²-8х≥0

2. Лежат ли точки В и А на окружности, заданной уравнением

3. Решить систему неравенств

4. Решить задачу: Мотоциклист ехал 3 ч по проселочной дороге и 0,5 ч по шоссе, всего он проехал 110 км. Скорость мотоциклиста на шоссе была на 10 км/ч больше, чем на проселочной дороге. С какой скоростью ехал мотоциклист по шоссе и с какой - по проселочной дороге?

3. Дана функция

А) укажите D(f);

Б) Найдите f(0); f(-1); f(4).

3. Даны векторы

Найти координаты вектора

3. Решить задачу по данному чертежу:

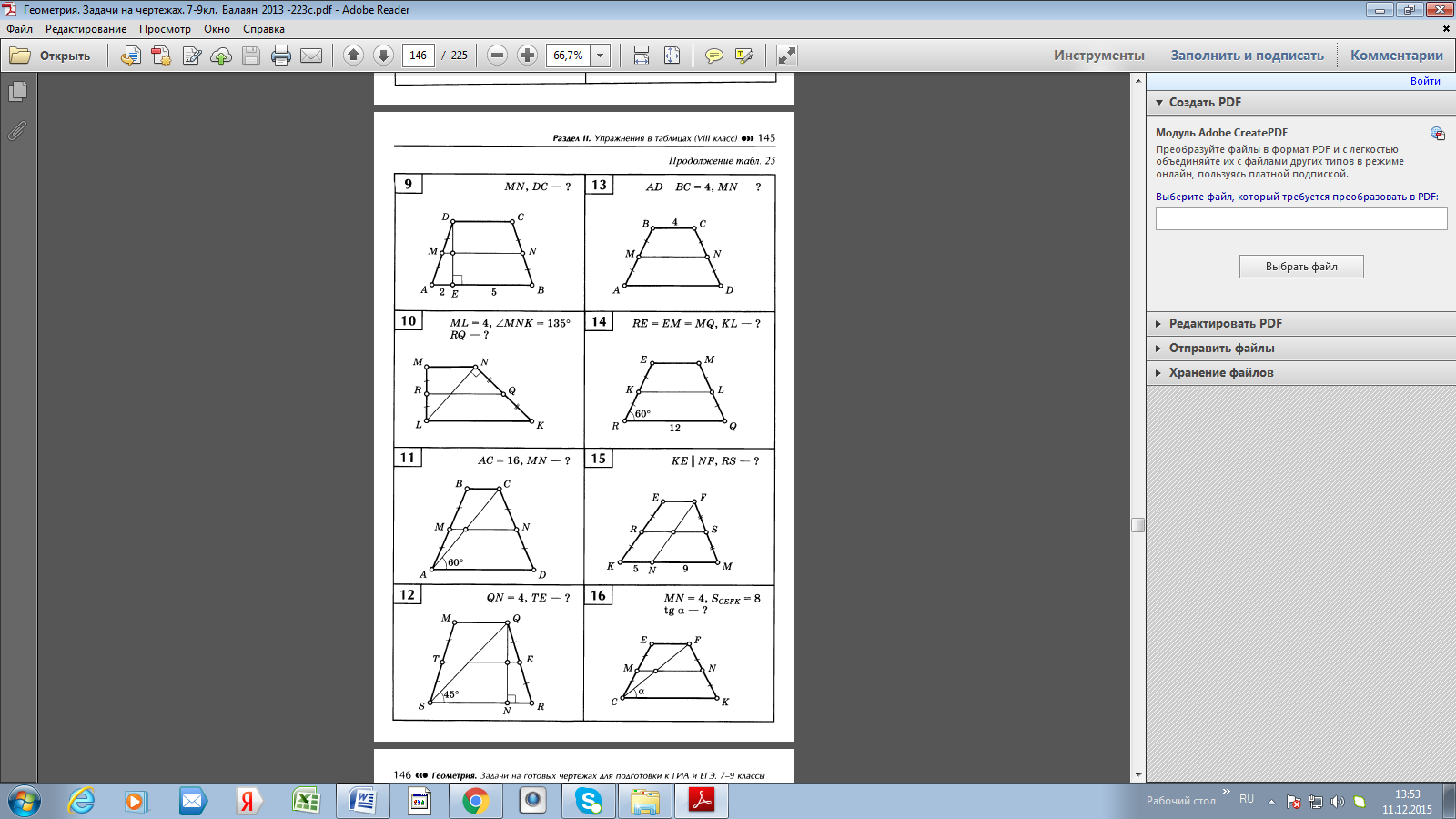
Контрольная работа за 1 полугодие 9 класса

Вариант 2

1. Решить неравенство

2. Лежат ли точки В и А на окружности, заданной уравнением

3. Решить систему неравенств

3. Решить задачу: Велосипедист ехал 2 часа по лесной дороге и 1,5 часа по шоссе. Всего он проехал 48 км. Скорость велосипедиста на шоссе была на 4 км/ч больше, чем на лесной дороге. С какой скоростью ехал велосипедист по шоссе и с какой - по лесной дороге?

3. Дана функция

А) укажите D(f);

Б) Найдите f(0); f(1); f(-3).

3. Даны векторы

Найти координаты вектора

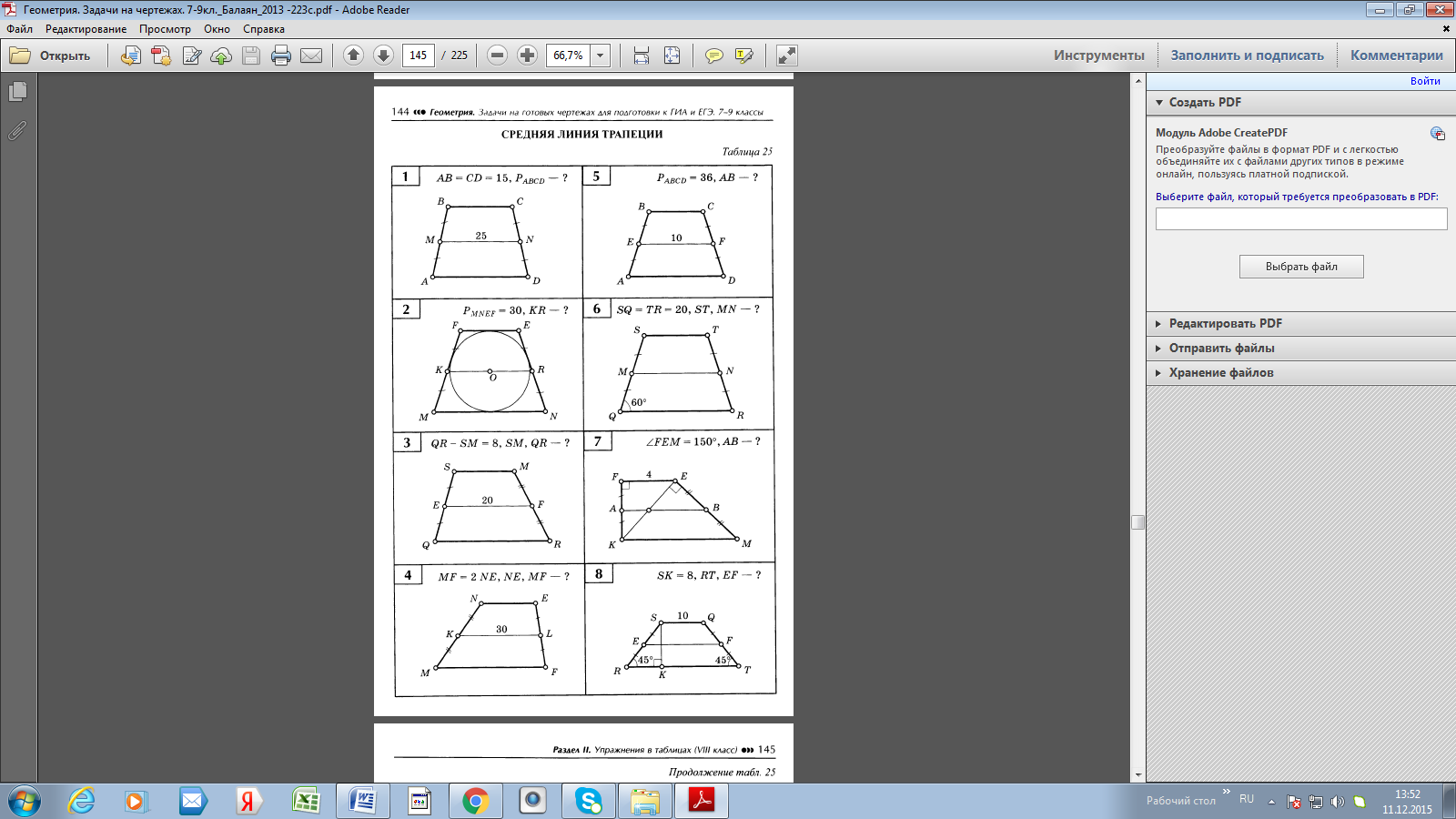
3. Решить задачу по данному чертежу:

Контрольная работа по математике по итогам 3 четверти 9 класс

Вариант 1

1 часть

1. Какое из чисел не является членом арифметической прогрессии 2; 5; 8; 11…?

1. 26 2) 30 3) 44 4) 122

2. В арифметической прогрессии (b_n) известны b₁=-1.2 и d=3. Найти b_21.

3. Найдите восьмой член геометрической прогрессии -28; 14…

4. Найдите углы правильного десятиугольника.

5. Найти площадь круга, если его радиус равен 1,1 см.

2 часть

6. Геометрическая прогрессия задана формулой n-го члена b_n=3ⁿ. Вычислить S₅.

7. Разность арифметической прогрессии равна 4. Сумма первых семи членов равна 651. Найдите первый член этой прогрессии.

8. Найдите разность арифметической прогрессии (с_n), если с₅=32, с₈=40.

9. Найдите площадь кругового сектора, если его радиус равен 7 см, а длина дуги равна 12 см.

10. Вокруг окружности описаны правильный треугольник и квадрат. Найдите отношение площадей этих фигур

Контрольная работа по математике по итогам 3 четверти 9 класс

Вариант 2

1 часть

1. Какое из чисел не является членом арифметической прогрессии 7; 12; 17; 22…?

1) 97 2) 107 3) 31 4) 52

2. В арифметической прогрессии (b_n) известны b₁=-0,8 и d=4. Найти b_7.

3. Найдите восьмой член геометрической прогрессии -18; -9…

4. Найдите углы правильного двадцатиугольника.

5. Найти площадь круга, если его радиус равен 1,3 см. Ответ округлите до десятых.

2 часть

2. Геометрическая прогрессия задана формулой n-го члена b_n=5^n-1. Найти S₅.

3. Разность арифметической прогрессии равна 5. Сумма восьми первых членов равна 1540. Найдите первый член этой прогрессии.

4. Найдите разность арифметической прогрессии (с_n), если с₉=2, с₂₁=-24.

5. Найдите площадь кругового сектора, если его радиус равен 8 см, а длина дуги равна 14 см.

6. Вокруг окружности описаны квадрат и правильный шестиугольник. Найдите отношение площадей этих фигур

Итоговая Контрольная работа.

Вариант 1

1) Упростите выражение .

2) Решить уравнения:

а) б)

в) г)

3) Решить неравенства:

а) б)

в)

4) Построить график функции



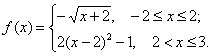
Записать свойства данной функции.

5) От турбазы до станции турист доехал на велосипеде за 3 часа. Пешком он смог бы пройти это расстояние за 7 часов. Известно, что пешком он идет со скоростью на 8 км/ч меньшей, чем едет на велосипеде. С какой скоростью ехал турист?

</<font face="Times New Roman, serif">Вариант 2

1) Упростите выражение .

2) Решить уравнения:

а) б)

в) г)

3) Решить неравенства:

а) б)

в)

4) Построить график функции



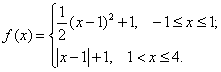
Записать свойства данной функции.

5) Два велосипедист отправились одновременно навстречу друг другу из двух пунктов, расстояние между которыми 60 км, и встретились через 2 ч. Определите скорость каждого велосипедиста, если у одного она на 2 км/ч больше, чем у другого.

27Математика 9 класс