- Учителю
- Тесты по основам анализа (раздел функциональный анализ)для специальности магистратуры Методика обучения математике
Тесты по основам анализа (раздел функциональный анализ)для специальности магистратуры Методика обучения математике
2-семестр Функциональный анализ. Магистратура
Составитель доцент Р.М.Тургунбаев
1. Укажите не верное утверждение.
-
*Если отображение F имеет слабую производную, то оно имеет и сильную производную и эти производные совпадают.
-
Если слабая производная
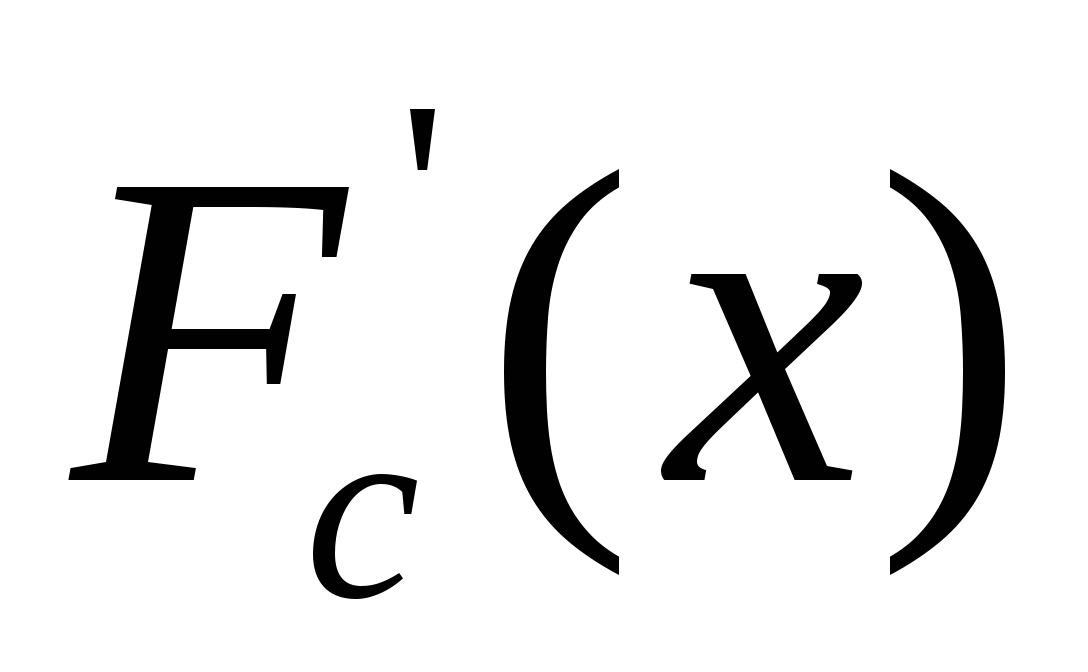 отображения F существует в некоторой U окрестности точки
x0 и представляет собой в этой окрестности
(операторную) функцию от x, непрерывную в точке x0,
то в точке x0 сильная производная F'(x0)
существует и совпадает со слабой.
отображения F существует в некоторой U окрестности точки
x0 и представляет собой в этой окрестности
(операторную) функцию от x, непрерывную в точке x0,
то в точке x0 сильная производная F'(x0)
существует и совпадает со слабой.
-
Если отображение
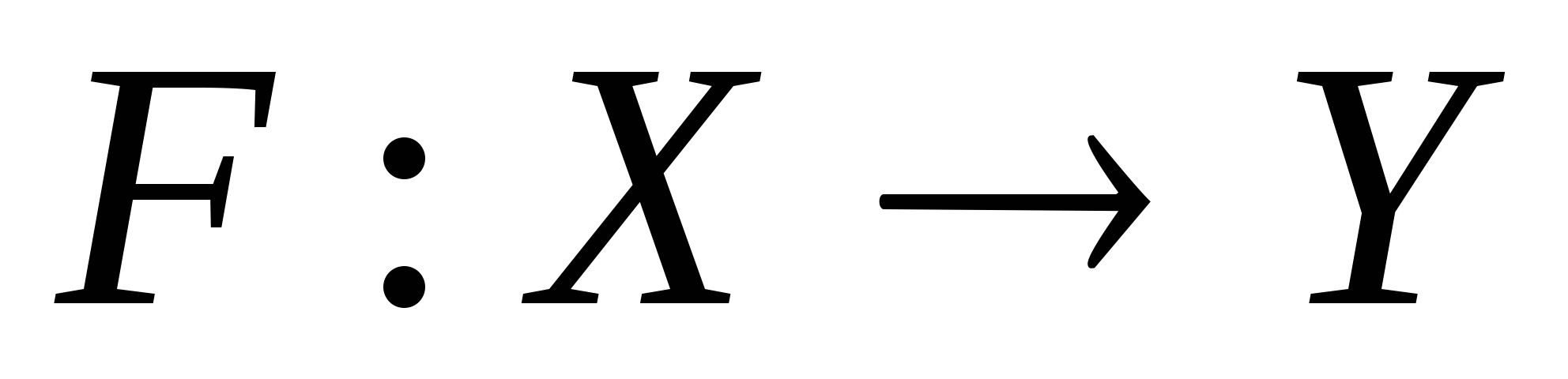 дифференцируемо в точке x, то оно обладает единственной
сильной производной.
дифференцируемо в точке x, то оно обладает единственной
сильной производной.
-
Если F(x) непрерывный линейный оператор, то его производная есть сам этот оператор.
2. Укажите не верное утверждение.
-
*Если F(x) непрерывный оператор, то его производная есть сам этот оператор.
-
Если слабая производная
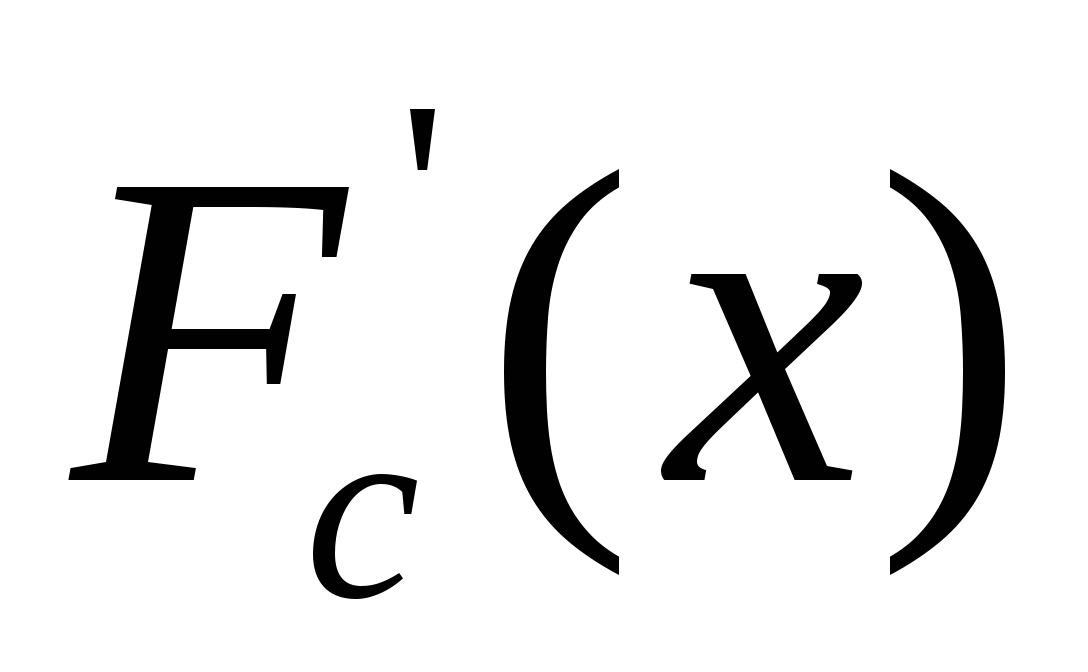 отображения F существует в некоторой U окрестности точки
x0 и представляет собой в этой окрестности
(операторную) функцию от x, непрерывную в точке x0,
то в точке x0 сильная производная F'(x0)
существует и совпадает со слабой.
отображения F существует в некоторой U окрестности точки
x0 и представляет собой в этой окрестности
(операторную) функцию от x, непрерывную в точке x0,
то в точке x0 сильная производная F'(x0)
существует и совпадает со слабой.
-
Если отображение F имеет сильную производную, то оно имеет и слабую, и они совпадают.
-
Если отображение
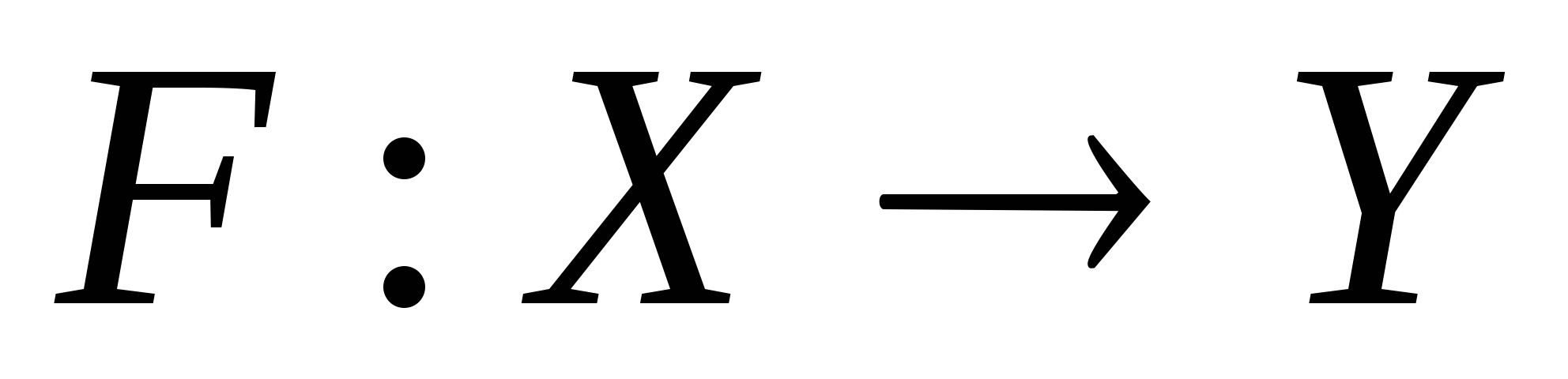 дифференцируемо в точке x, то оно обладает единственной
сильной производной.
дифференцируемо в точке x, то оно обладает единственной
сильной производной.
3. Пусть на Гильбертовом пространстве
H задан ограниченный оператор ![]() . Укажите какие условия являются необходимыми и достаточными
для того, чтобы оператор P был проектором 1)
. Укажите какие условия являются необходимыми и достаточными
для того, чтобы оператор P был проектором 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
-
*1 и 2
-
1 и 3
-
только 1
-
1 и 4
4. Пусть на Гильбертовом пространстве
H задан ограниченный оператор ![]() . Укажите какое условие является необходимым для того, чтобы
оператор P был проектором:
. Укажите какое условие является необходимым для того, чтобы
оператор P был проектором:
-
*
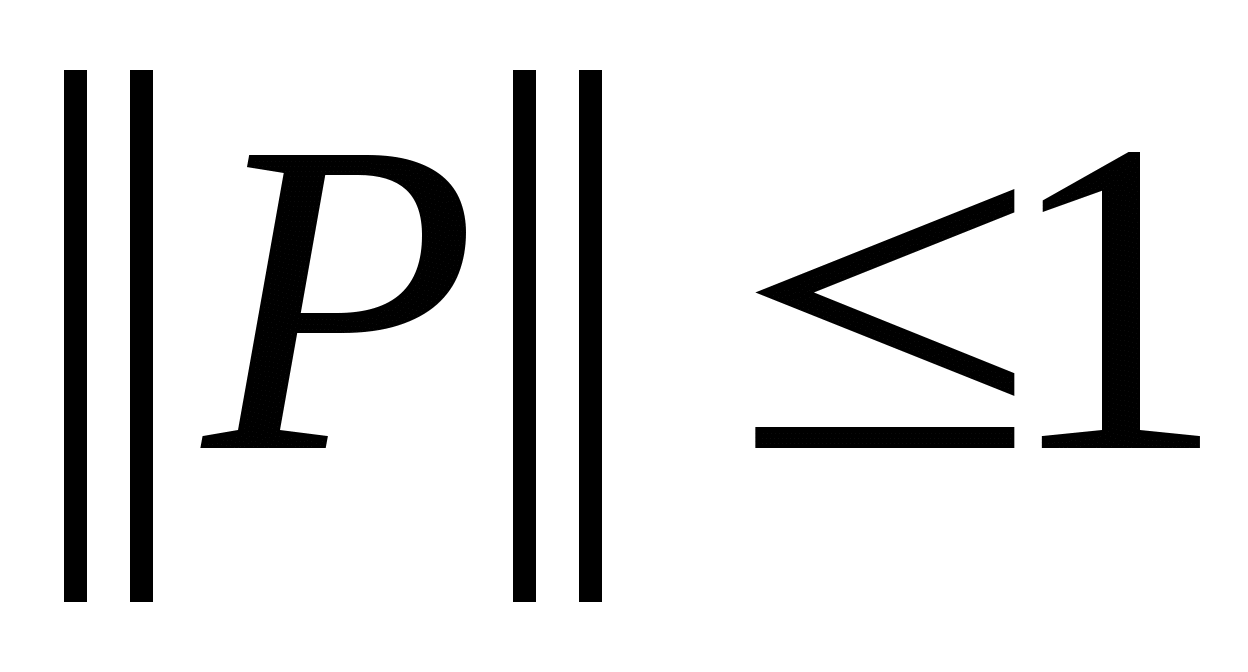
-
P2=0
-
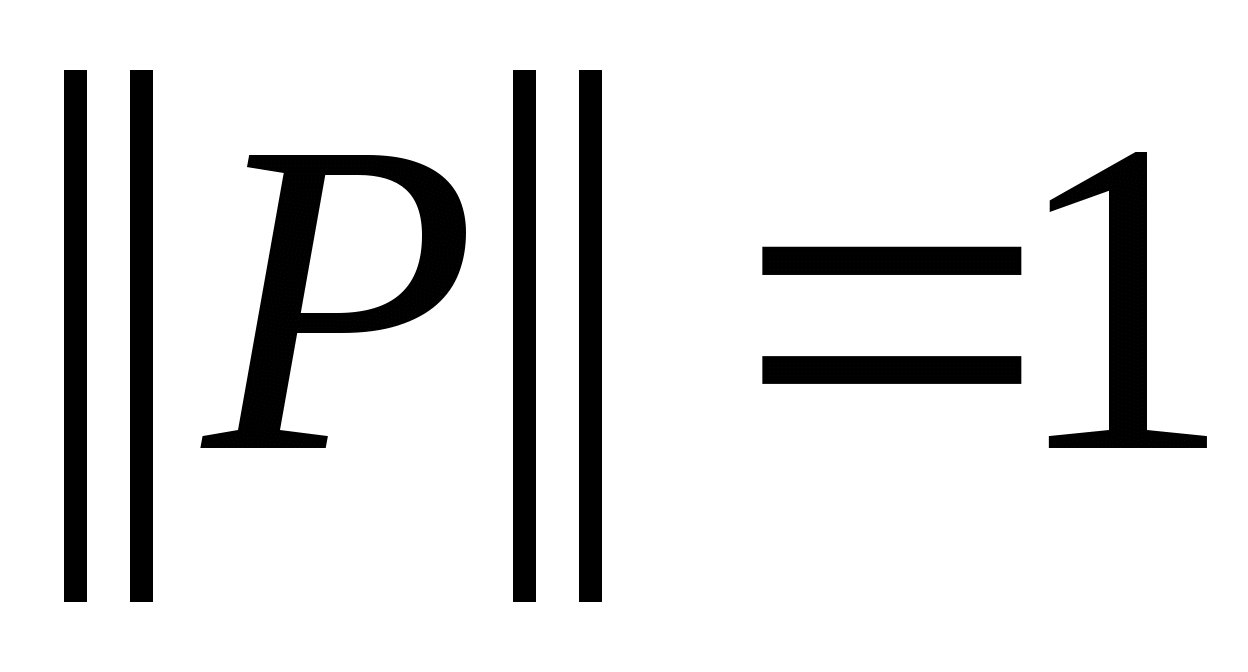
-
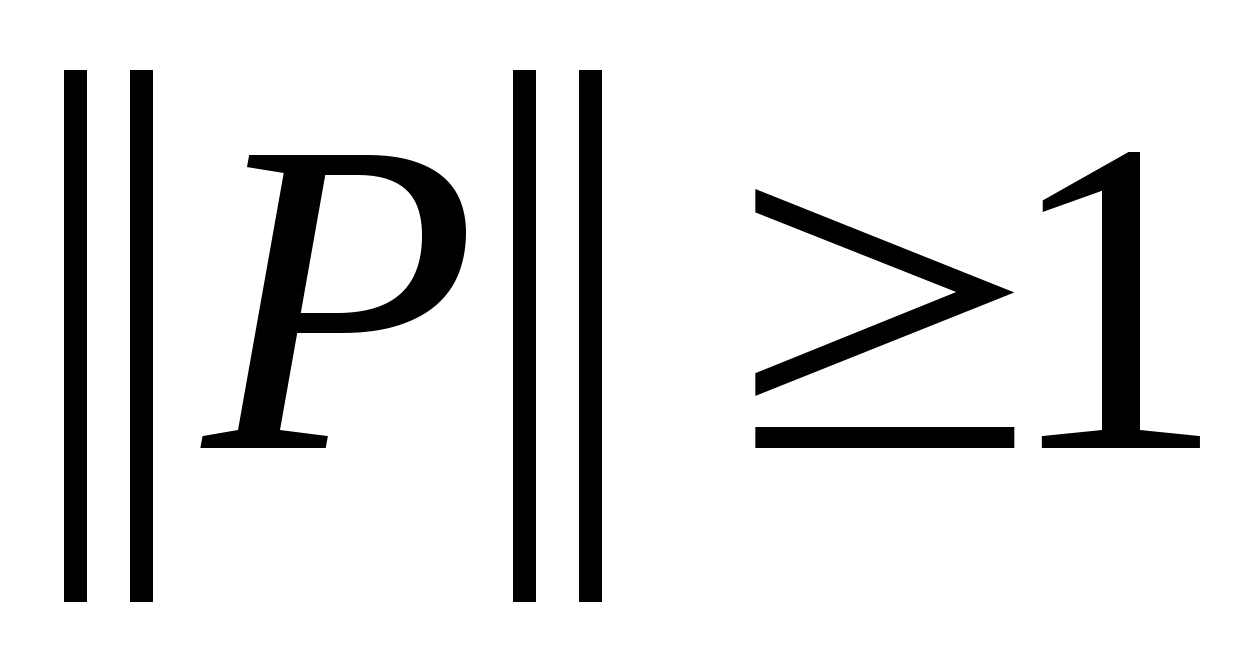
5. Укажите не верное утверждение. Если E банахово пространство и T:EE ограниченный линейный оператор, то
-
*
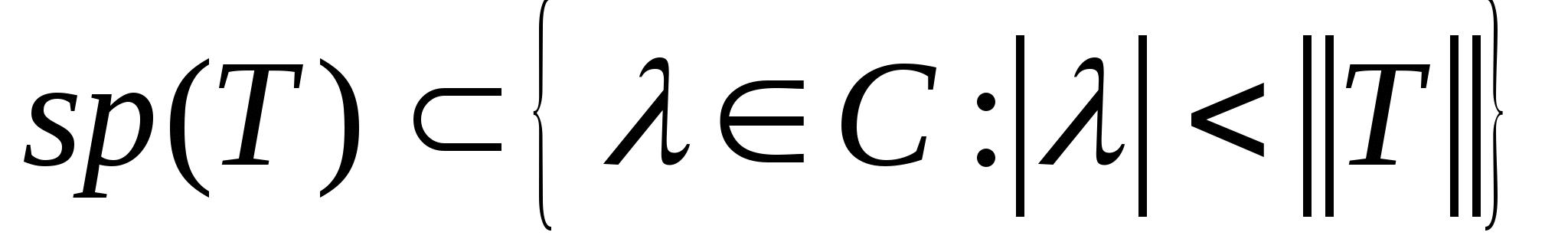
-
sp(T) замкнутое множество
-
sp(T) компактное множество
-
sp(T) не пустое множество
6. Найти спектр оператора A:
C[0,1]C[0,1], где 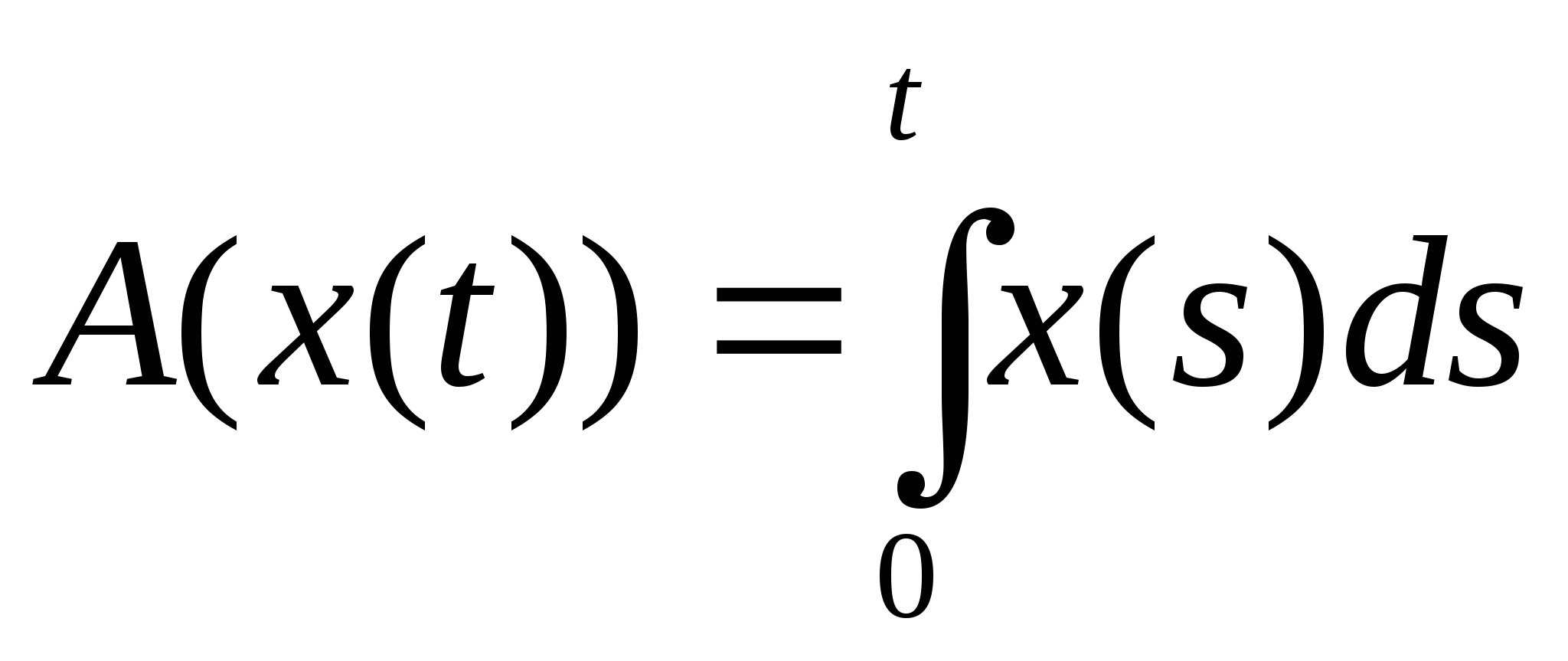 .
.
-
*{0}
-
{1}
-
[0,1]
-
7. Найти спектр оператора A:
C[0,1]C[0,1], где![]() .
.
-
*[0,1]
-
{0}
-
{1}
-
8. Найти спектр оператора A:
C[0,1]C[0,1], где ![]() .
.
-
*{0;1}
-
{0}
-
{1}
-
[0,1]
9. Укажите не верное утверждения для сильной производной.
-
*Если F(x) непрерывный линейный оператор, то его производная есть постоянное число.
-
Если F(x)=y0=const, то F'(x)
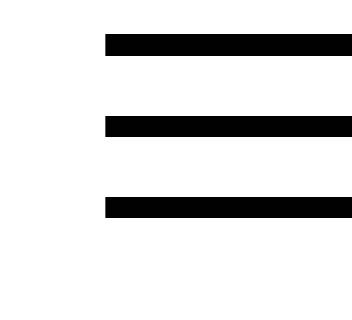 0
(нулевой оператор).
0
(нулевой оператор).
-
Если F(x) непрерывный линейный оператор, то его производная есть сам этот оператор.
-
Сильная производная единственна.
10. Укажите не верное утверждение.
-
*Если F(x) непрерывный линейный оператор, то его производная есть число.
-
Если слабая производная
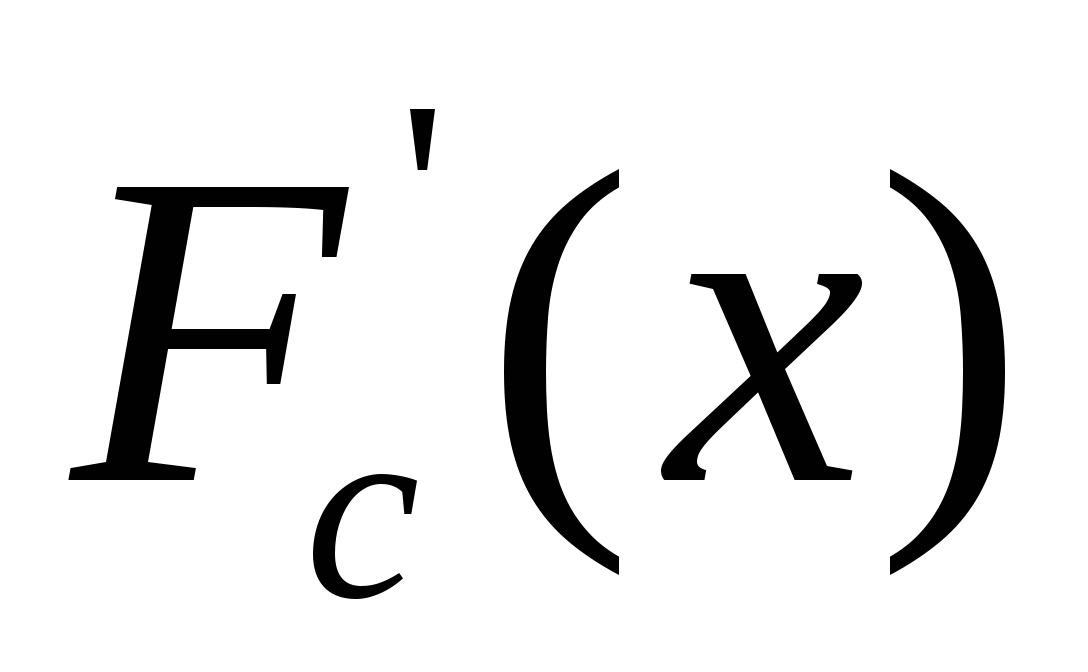 отображения F существует в некоторой U окрестности точки
x0 и представляет собой в этой окрестности
(операторную) функцию от x, непрерывную в точке x0,
то в точке x0 сильная производная F'(x0)
существует и совпадает со слабой.
отображения F существует в некоторой U окрестности точки
x0 и представляет собой в этой окрестности
(операторную) функцию от x, непрерывную в точке x0,
то в точке x0 сильная производная F'(x0)
существует и совпадает со слабой.
-
Если отображение F имеет сильную производную, то оно имеет и слабую, и они совпадают.
-
Если отображение
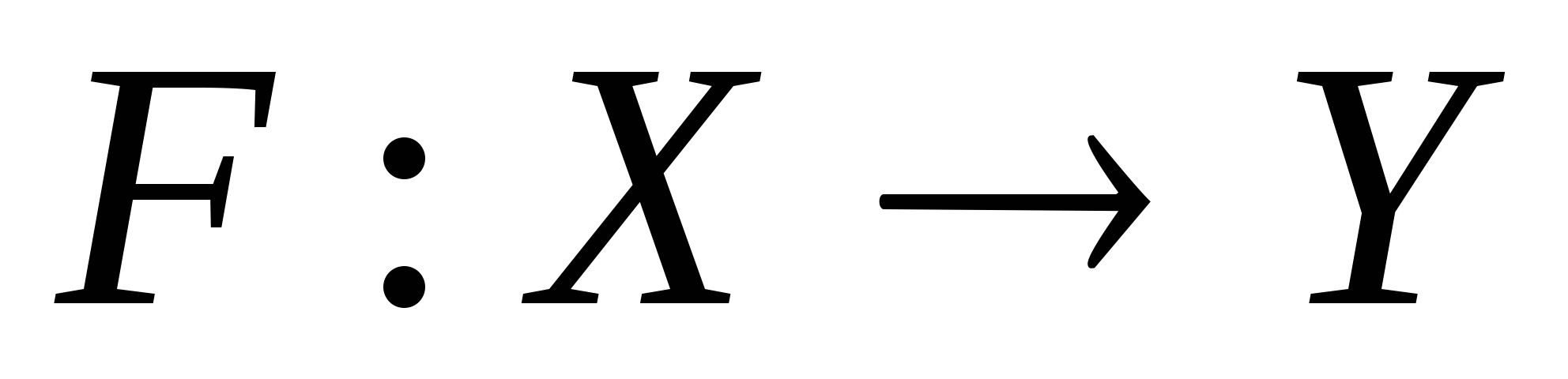 дифференцируемо в точке x, то оно обладает единственной
сильной производной.
дифференцируемо в точке x, то оно обладает единственной
сильной производной.
11. Если E и F банаховы пространства, ![]() ограниченный линейный оператор, то
ограниченный линейный оператор, то
A)* ![]() .
.
B) ![]()
C) ![]()
D) ![]()
12. Если Т оператор в гильбертовым пространстве H, то сопряженный оператор определяется следующим равенством.
A)* ![]()
B) ![]()
C) ![]()
D) ![]()
13. Пусть Н комплексное гильбертово
пространство. Какое свойство не верно для инволюции ![]() ?
?
A)* ![]() и
и ![]() - эрмитовы операторы;
- эрмитовы операторы;
B) ![]() ;
;
C) ![]() ;
;
D) ![]() ;
;
14. Пусть Н комплексное гильбертово
пространство. Какое свойство не верно для инволюции ![]() ?
?
A)* ![]() ;
;
B) ![]() ;
;
C) ![]() ;
;
D) ![]() - положительный оператор
- положительный оператор
15. Пусть Н комплексное гильбертово
пространство. Какое свойство верно для инволюции ![]() ?
?
A)* ![]() - положительный оператор
- положительный оператор
B)![]() ;
;
C) ![]() ;
;
D) ![]() и
и ![]() - Эрмитовы операторы;
- Эрмитовы операторы;
16. Пусть Н комплексное гильбертово
пространство. Какое свойство не верно для инволюции ![]() ?
?
A)* ![]() ;
;
B) если существует ![]() , то
, то ![]() .
.
C) ![]() единичный оператор;
единичный оператор;
D) ![]() - положительный оператор
- положительный оператор
17. Укажите верное утверждение. Линейный
оператор T отображает ![]() в
в ![]() и выражается матрицей
и выражается матрицей ![]() .
.
A) * тогда оператор T* выражается матрицей
![]() .
.
B) тогда оператор T* выражается матрицей
![]() .
.
C) тогда оператор T* выражается матрицей
![]() .
.
D) тогда оператор T* выражается матрицей
![]() .
.
18. Укажите верное утверждение. Линейный
оператор T отображает ![]() в
в ![]() и выражается матрицей
и выражается матрицей ![]() . для того чтобы оператор T был эрмитовым необходимо и достаточноб
чтобы выполнялось равенство
. для того чтобы оператор T был эрмитовым необходимо и достаточноб
чтобы выполнялось равенство
A) * ![]()
B) ![]()
C) ![]()
D) ![]()
19. Пусть ![]() комплексное Гильбертово пространство и
комплексное Гильбертово пространство и 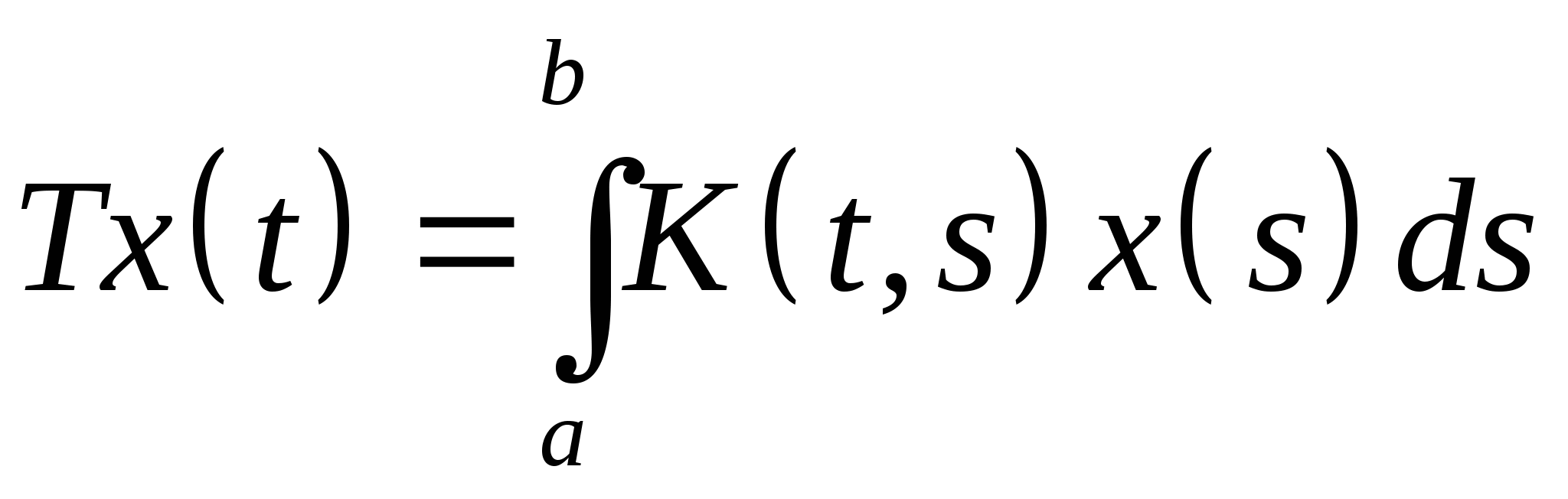 оператор Фредгольма. Найти сопряженный оператор.
оператор Фредгольма. Найти сопряженный оператор.
A)* 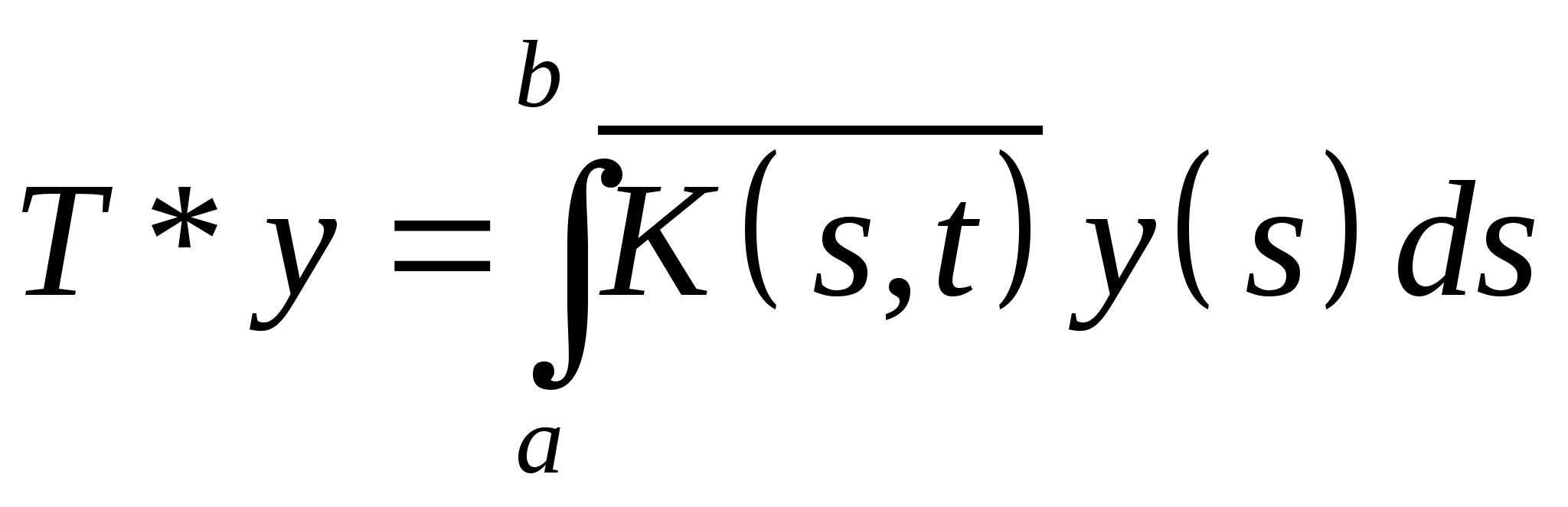
B) 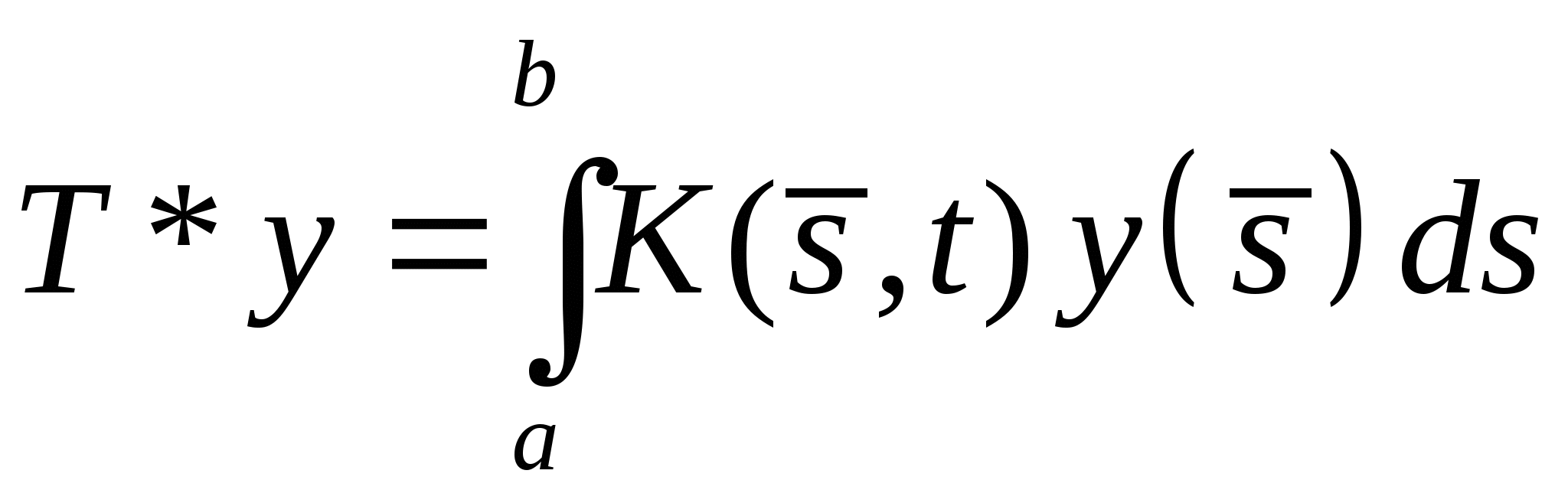
C) 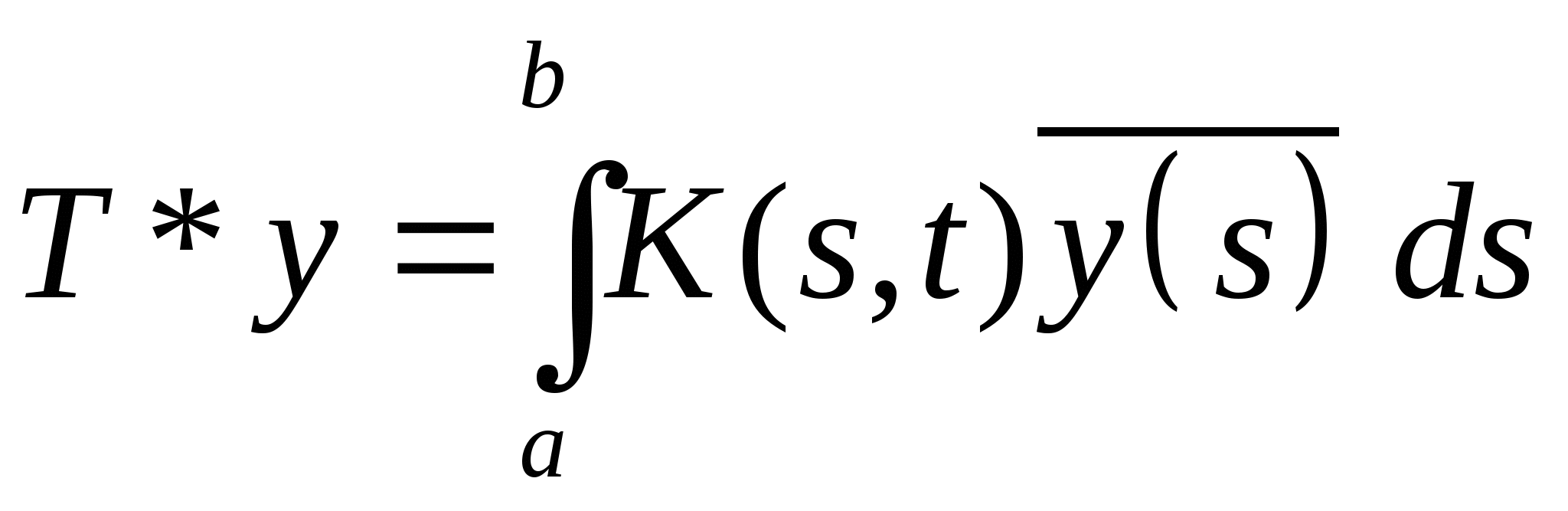
D) 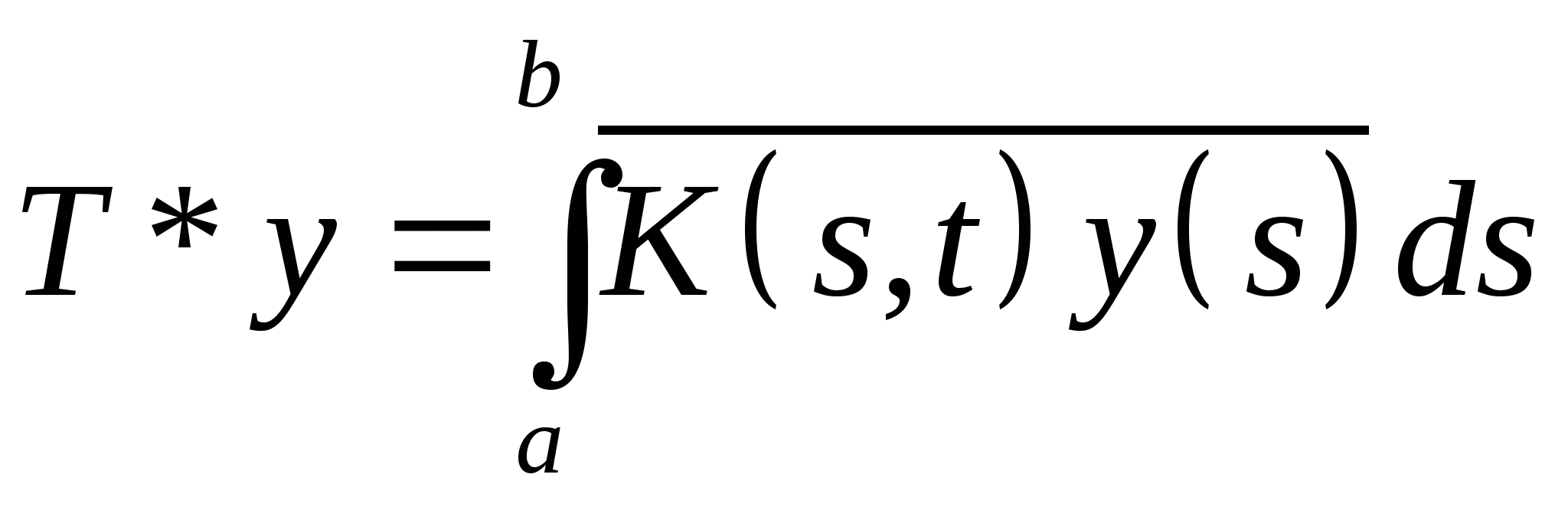
20. Пусть H гильбертово пространство над полем действительных чисел. Найдите производную Фреше функционала F(x)=||x||2.
A) * ![]()
B) ![]()
C) ![]()
D) не существует
21. Пусть H гильбертово пространство над полем действительных чисел. Найдите дифференциал функционала F(x)=||x||.
A)* (y,h)/||y||, y0, при y=0 не существует
B) (y,h)|, y0, при y=0 не существует
C) (y,h)/||y||
D) (y,h)
22. Пусть H гильбертово пространство над полем действительных чисел. Найдите дифференциал функционала F(x)=||x||2.
A) * ![]()
B) ![]()
C) ![]()
D) не существует
23. Напишите уравнение Эйлера функционала 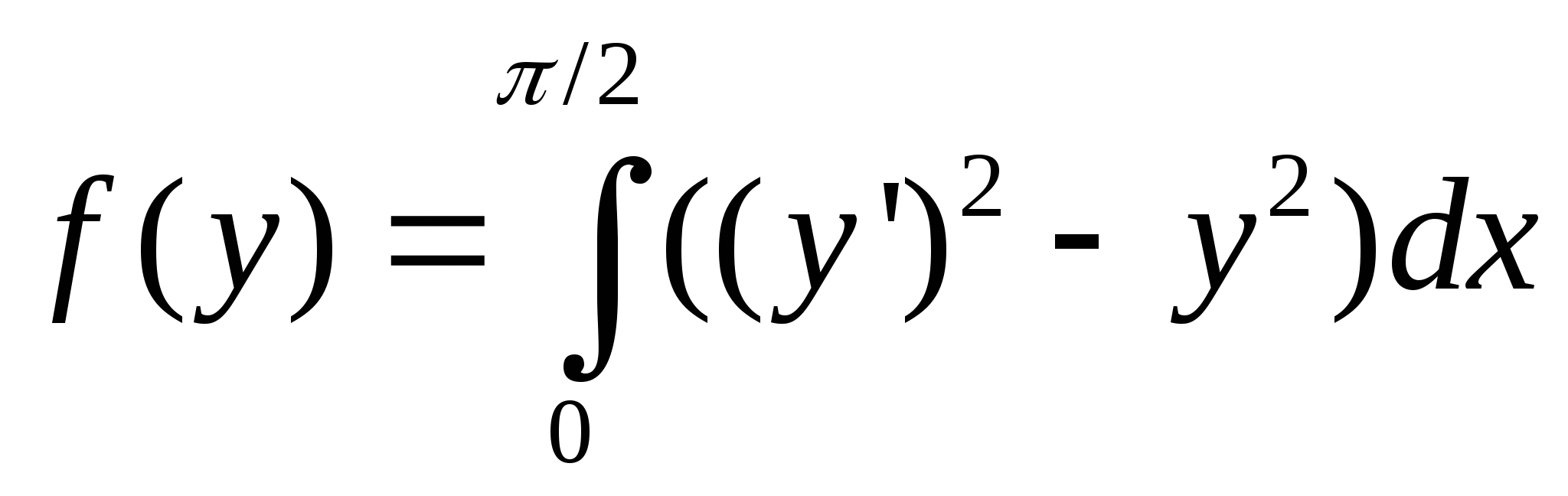
A)* y+y''=0
B)y-y''=0
C)y''-y=0
D)2y-y''=0
24. Напишите уравнение Эйлера функционала
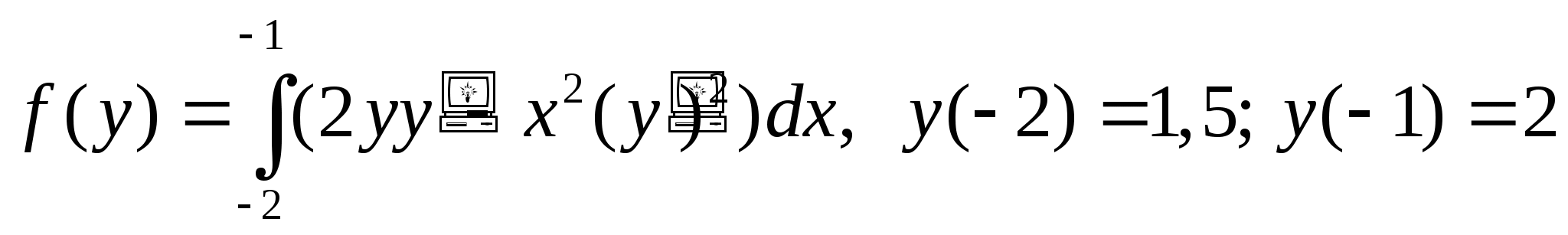
A)* ![]()
B) ![]()
C) ![]()
D) ![]()
25. Найдите экстремаль функционала 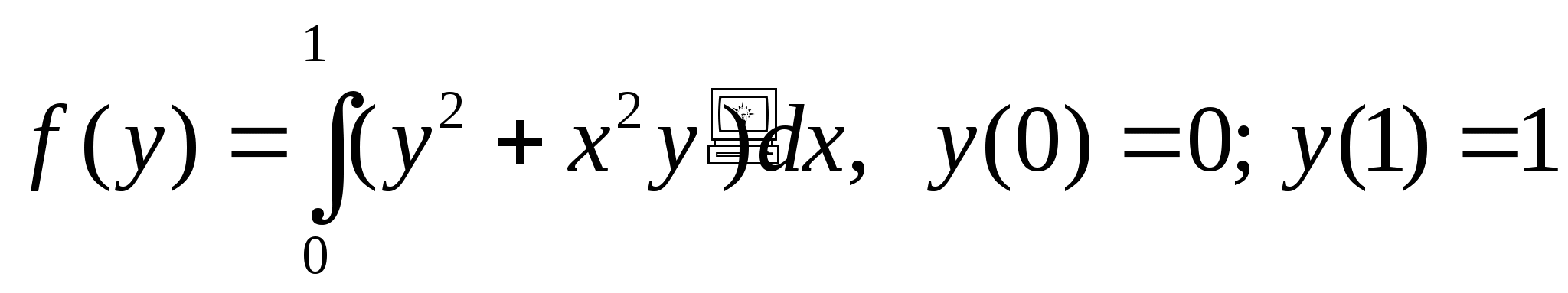
A)* y=x
B) y=-x
C) y=2x
D) не существует
26. Найдите экстремаль функционала 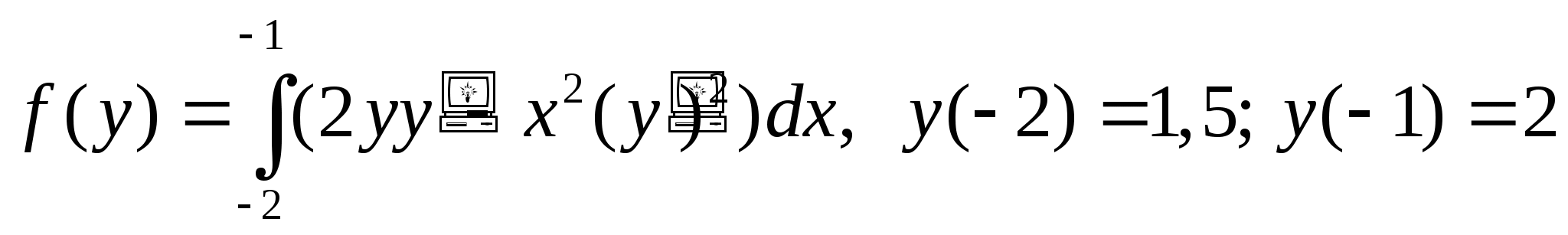
A)* ![]()
B) ![]()
C) ![]()
D) ![]()
27. Укажите верное утверждение. Пусть H комплексное гильбертово пространство, T самосопряженный оператор. Тогда собственные числа оператора Т
A)* вещественные числа.
B) положительные числа.
C) отрицательные числа.
D) комплексные числа.
28. Укажите верное утверждение. В пространстве
C[0,1] рассмотрим оператор ![]() . Тогда
. Тогда
A)* точечный спектр пустое множество, непрерывный спектр [0,1]
B) точечный спектр [0,1], непрерывный спектр пустое множество
C) точечный спектр пустое множество, непрерывный спектр {0,1}
D) точечный спектр {0,1}, непрерывный спектр пустое множество
29. Укажите не верное утверждение
A)* Всякий проектор в гильбертовом пространстве компактен
B) Непрерывный линейный оператор переводящий банахово пространство Е в некоторое его конечномерное подпространство компактен
C) В конечномерном нормированном пространстве всякий линейный оператор компактен
D) Оператор, сопряженный компактному компактен.
30. Какое утверждение не верно?
A)* В бесконечномерном пространстве Е компактный оператор имеет ограниченый обратный.
B) Если T компактный оператор, В -ограниченный, то операторы TB и BT компактны
C) Если {Tn}-последовательность компактных операторов в банаховом пространстве Е, сходящаяся по норме к некоторому оператору T, то опреатор T компактен.
D) Оператор, сопряженный компактному компактен
31. Укажите не верное утверждение.
A)* Производная непрерывного линейного оператора есть постоянное число.
B) Если F и G диференцируемы в некоторой точке
![]() , то
, то ![]()
C) Agar F дифференцируема в некоторой точке
![]() , то
, то ![]() .
.
D) Производная непрерывного линейного оператора есть сам этот оператор.
32. Укажите не верное утверждение.
A)* Если отображение F имеет слабую производную, то оно имеет и сильную, причем сильная и слабая производные совпадают.
B) Если отображение ![]() дифференцируема в некоторой точке x, оно имеет единственную
сильную производную
дифференцируема в некоторой точке x, оно имеет единственную
сильную производную
C) Если F(x)=y0=const, то
F'(x)![]() 0
0
D) Если отображение F имеет сильную производную, то оно имеет и слабую, причем сильная и слабая производные совпадают
33. Укажите не верное утверждение
A) * В конечномерном пространстве точечный спектр линейного оператора пуст
B) В конечномерном пространстве число
собственных чисел линейного оператора не боле ![]()
C) В конечномерном пространстве непрерывный спектр линейного оператора пуст
D) В конечномерном пространстве спектр линейного оператора состоит только из собственных чисел
34. Пусть E, F банаховы пространства и ![]() линейный оператор. Для того чтобы оператор Т обладал ограниченным
обратным оператором необходимо выполнения следующего условия
линейный оператор. Для того чтобы оператор Т обладал ограниченным
обратным оператором необходимо выполнения следующего условия
A)* Множество ![]() всюду плотно в F.
всюду плотно в F.
B) множество ![]() замкнуто
замкнуто
C) множество ![]() открыто
открыто
D) множество ![]() компактно
компактно
35. Пусть E, F банаховы пространства и ![]() линейный оператор. Для того чтобы оператор Т обладал ограниченным
обратным оператором необходимо выполнения следующего условия: для
некоторого C>0 и произвольного
линейный оператор. Для того чтобы оператор Т обладал ограниченным
обратным оператором необходимо выполнения следующего условия: для
некоторого C>0 и произвольного ![]() выполняется
выполняется
A)* ![]() .
.
B) ![]()
C) ![]()
D) ![]()
36. Пусть E, F банаховы пространства и ![]() линейный оператор. Для того чтобы оператор Т обладал ограниченным
обратным оператором необходимо выполнения следующего условия
линейный оператор. Для того чтобы оператор Т обладал ограниченным
обратным оператором необходимо выполнения следующего условия
A)*для некоторого C>0 и произвольного
![]() выполняется
выполняется ![]() .
.
B) для некоторого C>0 и некоторого ![]() выполняется
выполняется ![]()
C) для произвольного C>0 и произвольного
![]() выполняется
выполняется ![]()
D) для произвольного C>0 и некоторого
![]() выполняется
выполняется ![]()
37. Пусть Е банахово пространство,
I-тождественный оператор в Е, ![]() ограниченный оператор. Тогда для того чтобы выполнялось
соотношение
ограниченный оператор. Тогда для того чтобы выполнялось
соотношение 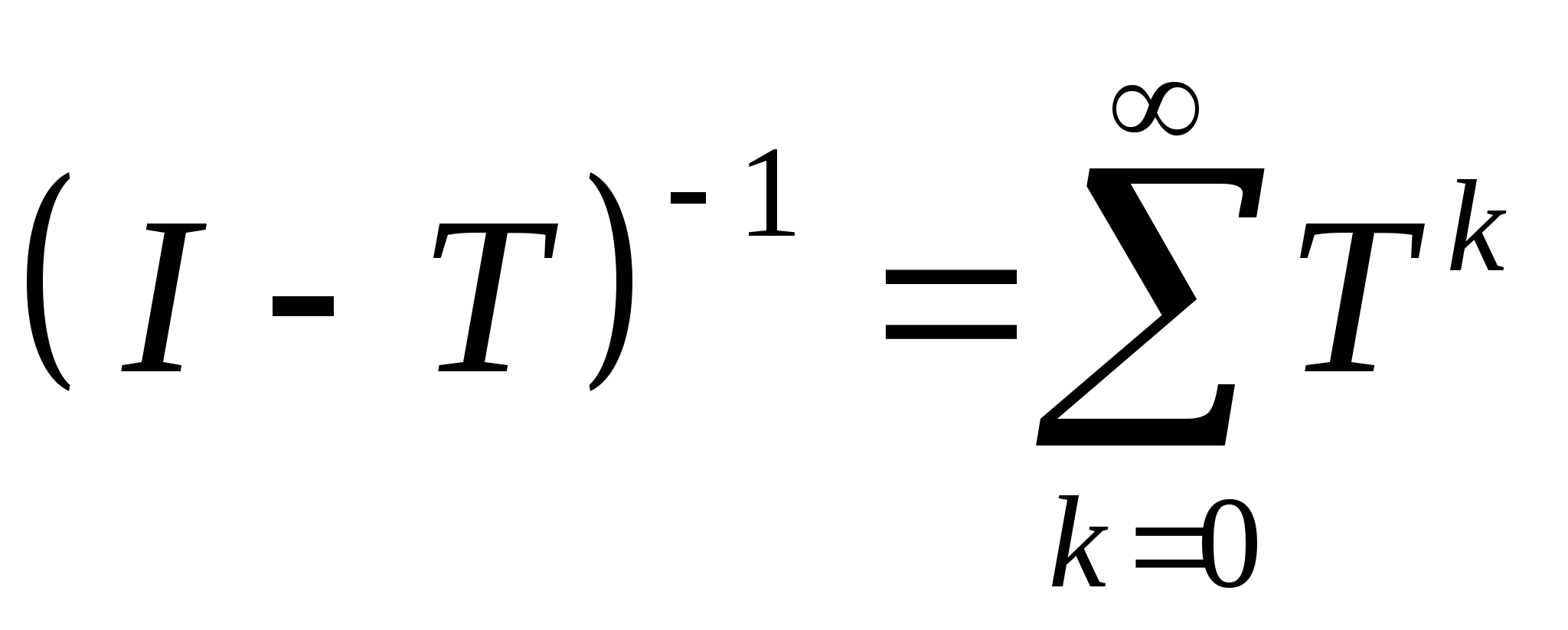
A) *достаточно, что ![]()
B) достаточно, что ![]()
C) достаточно, что ![]()
D) достаточно, что ![]()
38. Пусть Е банахово пространство,
I-тождественный оператор в Е, ![]() ограниченный оператор. Тогда для того чтобы существовал
ограниченный оператор. Тогда для того чтобы существовал ![]()
A) *достаточно, что ![]()
B) достаточно, что ![]()
C) достаточно, что ![]()
D) достаточно, что ![]()
39. Найти экстремали функционала.
А) * вариационная задача не имеет смысла
B)![]()
C) ![]()
D) ![]()
40. Исследовать на экстремум функционал 470с.11 а
А) * минимум при у=0
B) Минимум при у=1
C) Максимум при у=0
D) Максимум при у=1