- Учителю
- Рабочая программа по алгебре (10 класс)
Рабочая программа по алгебре (10 класс)
Муниципальное бюджетное общеобразовательное учреждение
«Любино-Малоросская средняя общеобразовательная школа»
Любинского муниципального района Омской области
Протокол №____ от 29 августа 2016г
Заместитель директора по УВР
____________ Е.С.Бондаренко
Утверждаю
Приказ № _____ от 31 августа 2016г
Директор МБОУ «Любино-Малоросская СОШ»
______________ Г.Ф.Сабранская
Рабочая программа по алгебре и началам математического анализа
10 класс
Составитель: Жакиянова Сауле Такенбаевна
учитель математики
высшей квалификационной категории
2016-2017 учебный год
П О Я С Н И Т Е Л Ь Н А Я З А П И С К А
Рабочая программа по алгебре и началам математического анализа для 10 класса составлена на основе:
-
Федеральный закон от 29 декабря 2012 года № 273-ФЗ «Об образовании в Российской Федерации»;
-
Федерального компонента государственного стандарта среднего общего образования на базовом уровне, утверждённого Приказом Министерства образования РФ от 5 марта 2004 года за №1089
-
Устав МБОУ «Любино-Малоросская СОШ», 2016г;
-
Программы общеобразовательных учреждений Алгебра и начала математического анализа 10 - 11классы, Москва «Просвещение» 2011г составитель Т.А. Бурмистрова
-
Приказ Министерства образования и науки РФ от 26 января 2016г №38 «О внесении изменений в федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования», утвержденный приказом Министерства образования и науки Российской Федерации от 31 марта 2014 г. № 253
-
Постановления Главного государственного санитарного врача Российской Федерации от 29 декабря 2010 г. N 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях». Зарегистрировано в Минюсте РФ 3 марта 2011 года. Регистрационный № 19993(редакции 2015г)
-
Концепция духовно-нравственного развития и воспитания личности гражданина России: учебное издание / А. Я. Данилюк, А. М. Кондаков, В. А. Тишков. - М. : Просвещение, 2011.
-
Методическое письмо ФИПИ «Методические рекомендации по некоторым аспектам совершенствования преподавания общеобразовательных предметов» (на основе анализа типичных затруднений выпускников при выполнении заданий ЕГЭ), 2015 год.
-
Учебного плана МБОУ «Любино - Малоросская СОШ» на 2016/2017 учебный год
Школьное образование в современных условиях призвано обеспечить функциональную грамотность и социальную адаптацию обучающихся на основе приобретения ими компетентностного опыта в сфере учения, познания, профессионально-трудового выбора, личностного развития, ценностных ориентаций и смыслотворчества. Это предопределяет направленность целей обучения на формирование компетентной личности, способной к жизнедеятельности и самоопределения в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути.
Главной целью школьного образования является развитие ребенка как компетентной личности путем включения его в различные виды ценностной человеческой деятельности: учеба, познания, коммуникация, профессионально-трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности. С этих позиций обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями. Это определило цели обучения математике:
-
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
-
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
-
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
-
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
На основании требований Государственного образовательного стандарта 2004 г. в содержании календарно-тематического планирования предполагается реализовать актуальные в настоящее время компетентностный, личностно ориентированный, деятельностный подходы, которые определяют задачи обучения:
-
приобретение математических знаний и умений;
-
овладение обобщенными способами мыслительной, творческой деятельностей;
• освоение компетенций (учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной) и профессионально-трудового выбора.
. Авторская программа рассчитана по 1 варианту на 85ч, по 2 варианту на 136 часов. На основании учебного плана школы на 2016/2017 учебный год на курс алгебры в 10 классе отводится 3 часа в неделю. Внесена корректировка в тематическое планирование: увеличено количество часов на следующие темы «Степень с действительным показателем» на 2 часа, «Степенная функция» на 3 часа, «Показательная функция» на 5 часов, «Логарифмическая функция» на 5 часов, «Тригонометрические уравнения» на 1 час. Так как в 10 классе по программе не предусмотрены часы на повторение. В планирование учебного материала внесено изменение и предусмотрены часы на раздел «Повторение» - 5часов. Всего 21 час.
Содержание рабочей программы направлено на освоение обучающимися знаний, умений и навыков на базовом уровне. Она включает в себя все темы, предусмотренные федеральным компонентом государственного образовательного стандарта среднего общего образования по математике. Преобладающими формами текущего контроля выступают письменный и устный опросы, самостоятельные и контрольные работы, тестирование. Контрольных работ - 6. Промежуточный контроль - итоговая контрольная работа.
Основной целью является обновление требований к уровню подготовки выпускников в системе образования, отражающее важнейшую особенность педагогической концепции государственного стандарта - переход от суммы «предметных результатов» (то есть образовательных результатов, достигаемых в рамках отдельных учебных предметов) к межпредметным и интегративным результатам. Такие результаты представляют собой обобщенные способы деятельности, которые отражают специфику не отдельных предметов, а ступеней общего образования. В государственном стандарте они зафиксированы как общие учебные умения, навыки и способы человеческой деятельности, что предполагает повышенное внимание к развитию межпредметных связей курса алгебры и начал анализа.
При изучении алгебры и начал анализа в старшей школе осуществляется переход от методики поурочного планирования к модульной системе организации учебного процесса. Модульный принцип позволяет не только укрупнить смысловые блоки содержания, но и преодолеть традиционную логику изучения математического материала: от единичного к общему и всеобщему и от фактов к процессам и закономерностям. В условиях модульного подхода возможна совершенно иная схема изучения математических процессов «все общее - общее - единичное».
Специфика целей и содержания изучения алгебры и начал анализа существенно повышает требования к рефлексивной деятельности учащихся: к объективному оцениванию своих учебных достижений, поведения, черт своей личности, способности и готовности учитывать мнения других людей при определении собственной позиции и самооценке, понимать ценность образования как средства развития культуры личности.
Курс реализуется через учебник Алгебра и начала математического анализа, 10 класс. Ю.М.Колягин, М.В. Ткачева, Н.Е.Федорова, М.И.Шабунин, Москва «Просвещение», 2009 - 2011г.
Требования к уровню подготовки обучающихся 10 классов
В результате изучения алгебры и начала анализа на базовом уровне ученик должен
знать/понимать:
- значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов и исследованию процессов и явлений в природе и обществе;
-
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа;
-
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
- вероятностный характер различных процессов окружающего мира.
уметь
-
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций;
-
описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
-
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
Начала математического анализа
уметь
-
исследовать в простейших случаях функции на монотонность
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь
-
решать рациональные, показательные и логарифмические уравнения и неравенства,
-
составлять уравнения и неравенства по условию задачи;
-
использовать для приближенного решения уравнений и неравенств графический метод;
-
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
построения и исследования простейших математических моделей;
Календарно - тематическое планирование (Алгебра - 10)
Тема урока
Элементы содержания
Требования к уровню подготовки учащихся
Дата проведения
план
фактически
Глава IV Степень с действительным показателем 13ч
1
Действительные числа
Действительные числа
Знать определение действительного числа
2 - 4
Бесконечно - убывающая геометрическая прогрессия
Бесконечно убывающая геометрическая прогрессия.
Формула суммы бесконечно убывающей геометрической прогрессии.
Знать понятие бесконечно убывающей геометрической прогрессией; формулу суммы бесконечно-убывающей геометрической прогрессии
Уметь находить сумму бесконечной убывающей геометрической прогрессии
Сумма бесконечно убывающей геометрической прогрессии.
С\р «Бесконечно - убывающая геометрическая прогрессия»
5 - 7
Арифметический корень натуральной степени
Корень n-степени из неотрицательного числа, извлечение корня, подкоренное выражение, показатель корня, радикал
Иметь представление об определении корня n-степени, его свойствах.
Уметь выполнять преобразования выражений, содержащих радикалы; решать простейшие уравнения, содержащие корни n-степени;
Свойства арифметического корня натуральной степени
С\р «Арифметический корень натуральной степени»
8 - 11
Степень с рациональным показателем
Степень с рациональным показателем и её свойства. Степень с действительным показателем
Знать свойства корня степени с рациональным показателем.
Уметь преобразовывать простейшие выражения, содержащие радикалы; находить значения степени с действительным показателем; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени
Степень с действительным показателем
С\р «Степень с рациональным и действительными показателями»
12
Решение задач по теме: «Степень с действительным показателем»
13
Контрольная работа № 1 «Степень с действительным показателем»
Глава V СТЕПЕННАЯ ФУНКЦИЯ (16ч)
14 - 16
Степенная функция, её свойства.
Степенные функции, свойства функции, график степенной функции
Знать, как строить графики степенных функций при раз-
личных значениях показателя.
Уметь строить графики степенных функций при различных значениях показателя; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения
Степенная функция, её свойства и график
С\р «Степенная функция, её свойства и график»
17 - 18
Взаимно - обратные функции. Сложные функции
Уметь находить функцию, обратную данной.
Знать, что графики взаимно обратных функций симметричны относительно прямой у = х
Р/з Взаимно - обратные функции. Сложные функции
19 - 20
Дробно - линейная функция
Р/з «Дробно - линейная функция»
21 - 24
Равносильные уравнения
Равносильность
уравнений, следствие уравнений, посторонние корни, теорема о равносильности, преобразование данного уравнения в уравнение-следствие, расширение области определения, проверка корней, потеря корней
Иметь представление о равносильности уравнений.
Знать основные теоремы равносильности.
Уметь объяснить изученные положения на самостоятельно подобранных конкретных примерах (Р)
Равносильные неравенства
Равносильные систем
С\р «Равносильные уравнения и неравенства»
25 - 26
Иррациональные уравнения
Иррациональные уравнения, методы решения иррациональных уравнений
Уметь:
- решать простые иррациональные уравнения стандартными методами; обосновывать суждения, давать определения, приводить доказательства, примеры;
С\р «Иррациональные уравнения»
27 - 28
Решение задач по теме «Степенная функция»
Решение задач по теме «Равносильные уравнения и неравенства»
29
Контрольная работа № 2 «Степенная функция»
Глава VI Показательная функция 15ч
30 - 32
Показательная функция, её свойства и график
Показательная функция, степень с произвольным действительным показателем, свойства показательной функции, график функции, симметрия относительно оси ординат, экспонента.
Иметь представление о показательной функции, ее свойствах и графике.
Знать определения показательной функции.
Уметь:
- определять значение функции по значению аргумента при различных способах задания функции; строить график функции; формулировать её свойства, строить схематический график любой показательной функции;
Показательная функция, график
С\р «Показательная функция, её свойства и график»
33 - 36
Показательные уравнения
Показательное уравнение, функционально-графический
метод, метод уравнивания показателей, метод введения новой переменной
Иметь представление о показательном уравнении.
Знать показательные уравнения. Уметь решать простейшие показательные уравнения; использовать для приближенного решения уравнений графический метод
Способы решения показательных уравнений
Р/з «Показательные уравнения»
С/р «Показательные уравнения»
37 - 39
Показательные неравенства
Показательные неравенства, методы
решения показательных неравенств, равносильные неравенства
Иметь представление о показательном неравенстве.
Уметь решать простейшие показательные неравенства, их системы; использовать для приближенного решения неравенств графический метод
Методы решения показательных неравенств
Равносильные неравенства
40- 41
Системы показательных уравнений
Система уравнений и неравенств, решение системы
Уравнений и неравенств, равносильные системы, методы решения систем уравнений и неравенств
Знать, как графически и аналитически решать системы уравнений и неравенств.
Уметь
- работать с учебником, отбирать и структурировать материал;
- графически и аналитически решать системы уравнений и неравенств;
Системы показательных неравенств
42 - 43
Решение задач по теме «Показательная функция»
Знать о различных методах решения уравнений, неравенств и их систем.
Уметь:
- использовать свойства и графики показательной функции, решать показательные уравнения и неравенства
Решение задач по теме «Показательные уравнения»
44
Контрольная работа № 3 «Показательная функция»
Глава VII Логарифмическая функция 20ч
45 - 46
Логарифмы
Логарифм, основание логарифма, иррациональное число, логарифмирование, десятичный и натуральный логарифмы, основное логарифмическое тождество
Знать, как использовать связь между степенью и логарифмом, понимать их взаимно противоположное значение.
Уметь:
- устанавливать связь между степенью и логарифмом, понимать их взаимно противоположное значение, вычислять логарифм числа по определению;
Десятичный и натуральный логарифмы
47 - 49
Свойства логарифмов
Свойства логарифмов, логарифм произведения, логарифм частного, логарифм степени, логарифмирование
Знать свойства логарифмов.
Уметь
- выполнять арифметические действия, сочетая устные и письменные приемы;
- находить значения логарифма;
- проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы
Р/з «Свойства логарифмов»
С/р «Свойства логарифмов»
50 - 51
Десятичные и натуральные логарифмы.
Десятичные и натуральные логарифмы.
Формулы пере хода
52 - 54
Логарифмическая функция, её свойства
Логарифмическая функция, логарифмическая кривая, свойства логарифмической функции, график функции
Знать, как применить определение логарифмической функции, ее свойства в зависимости от основания.
Уметь определять значение функции по значению аргумента при различных способах задания функции
Логарифмическая функция и её график
С\р «Логарифмическая функция, её свойства»
55 - 58
Логарифмические уравнения
Логарифмическое уравнение, потенцирование, равносильные логарифмические уравнения, функционально-графический метод, метод потенцирования, метод введения новой переменной, метод логарифмирования
Знать о методах решения логарифмических уравнений.
Уметь решать простейшие логарифмические уравнения, использовать метод введения новой переменной для сведения уравнения к рациональному виду
Способы решения логарифмических уравнений
Р/з «Логарифмические уравнения»
С/р «Логарифмические уравнения»
59 - 61
Логарифмические неравенства
Логарифмическое неравенство, равносильные логарифмические неравенства, методы
решения логарифмических неравенств
Знать алгоритм решения логарифмического неравенства
в зависимости от основания. Уметь решать простейшие логарифмические неравенства, применяя метод замены переменных для сведения логарифмического неравенства к рациональному виду
Равносильные логарифмические неравенства
Р/з «Логарифмические неравенства»
62 - 63
Решение задач по теме «Логарифмическая функция»
Знать о понятии логарифма, его свойствах; о функции, ее свойствах и графике; о решении простейших логарифмических уравнений и неравенств
Решение задач по теме «Логарифмические уравнения и неравенства»
64
Контрольная работа № 4 «Логарифмическая функция»
Глава VIII Тригонометрические формулы 20ч
65
Радианная мера угла
Радианная мера угла. Числовая окружность, положительное и отрицательное направление обхода окружности.
Знать, понятия:
- числовая окружность
- радиан, радианная мера угла;
- соотношения между градусной и радианной мерами угла.
Уметь:
- найти на числовой окружности точку, соответствующую данному числу;
- заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц;
- составить таблицу для точек числовой окружности и их координат;
-
по координатам находить точку числовой окружности;
66 - 67
Поворот точки вокруг начала координат
Р/з «Поворот точки вокруг начала координат»
68 - 69
Определение синуса, косинуса и тангенса
Синус, косинус, тангенс и их свойства, первая, вторая, третья и четвертая четверти окружности
Знать понятие синуса, косинуса, тангенса произвольного угла; радианную меру угла.
Уметь:
- вычислить синус, косинус, тангенс числа;
- вывести некоторые свойства синуса, косинуса;
Р/з «Определение синуса, косинуса и тангенса»
70
Знаки синуса, косинуса и тангенса
71 - 72
Зависимость между синусом, косинусом и тангенсом одного и того же
Тригонометрические функции числового аргумента, тригонометрические соотношения одного аргумента
Уметь:
-
совершать преобразования простых тригонометрических выражений, зная основные тригонометрические тождества;
Р/з «Зависимость между синусом, косинусом и тангенсом одного и того же угла»
73 - 74
Тригонометрические тождества
Тождество
Знать определение тождества.
Уметь:
-совершать преобразования простых тригонометрических выражений, зная основные тригонометрические тождества; применять способы доказательства тождеств при решении задач
Р/з «Тригонометрические тождества»
75
Синус, косинус и тангенс углов
Синус, косинус, тангенс отрицательного угла
Знать формулы sin(-)=-sin, cos(-)=cos, tg(-)=-tg
Уметь применять при решении задач
76 - 77
Формулы сложения
Формулы синуса и
косинуса, тангенса суммы и разности аргументов, вывод формул
С/р «Формулы сложения»
78
Синус, косинус и тангенс двойного угла
Формулы двойного аргумента, формулы половинного угла, формулы кратного аргумента
Знать формулы двойного угла синуса, косинуса и тангенса.
Уметь:
- применять формулы для упрощения выражений;
- объяснить изученные положения на самостоятельно подобранных конкретных примерах (
Знать формулу синуса, косинуса, тангенса суммы и разности двух углов.
Уметь:
-преобразовывать простейшие выражения, используя основные тождества, тригонометрические выражения;
-передавать информацию сжато, полно, выборочно;
-излагать информацию, интерпретируя факты, разъясняя значение и смысл теории
79
Синус, косинус и тангенс половинного угла
Знать формулу синуса, косинуса, тангенса суммы и разности двух углов.
Уметь:
- преобразовывать простейшие выражения, используя основные тождества, тригонометрические выражения;
-извлекать необходимую информацию из учебно-научных текстов;
-формировать вопросы, задачи, создавать проблемную ситуацию;
-подбирать аргументы для доказательства своего решения, оформлять и выполнять тестовые задания
80 - 81
Формулы приведения
Формулы приведения, углы перехода
Знать вывод формул приведения.
Уметь: упрощать выражения, используя основные тригонометрические тождества и формулы приведения;
Р/з «Формулы приведения»
82
Сумма и разность синусов. Сумма и разность косинусов
Знать формулу суммы и разности синусов и суммы и разности косинусов.
Уметь применять формулы для преобразования простейших тригонометрических выражений.
83
Решение задач по теме «Тригонометрические формулы»
Формулы приведения, углы перехода
Уметь:
-преобразовывать простейшие выражения, используя основные тождества, формулы приведения;
- расширять и обобщать сведения о преобразовании тригонометрических выражений, применяя различные формулы;
84
Контрольная работа № 5 «Тригонометрические формулы»
Глава IX Тригонометрические уравнения 16ч
85 - 87
Уравнение cos t = а
Уравнение cos t = a, простейшие тригонометрические
уравнения
Знать формулу решения уравнения
Уметь:
- решать простейшие уравнения cos t = а;
Р/з «Уравнение cos t = а
С/р «Уравнение cos t = а»
88 - 90
Уравнение sin х = а,
уравнение sin t = а, простейшие тригонометрические уравнения
Знать формулу решения уравнения
Уметь:
-решать простейшие уравнения
sin t = а
Р/з «Уравнение sin х = а»
91 - 93
Уравнение: tg х = a
уравнения: tg t = a,
сtg t = а, простейшие тригонометрические уравнения.
Знать формулу решения уравнения
Уметь:
-решать простейшие уравнения tg х = а и ctg х = а;
Уравнение: сtg х = а
Р/з «Уравнение: tg х = a, сtg х = а»
94 - 96
Тригонометрические уравнения, сводящиеся к алгебраическим.
Простейшие тригонометрические уравнения, метод введения новой переменной, метод разложения на множители, однородные тригонометрические уравнения, алгоритм решения однородного уравнения второй степени
Уметь:
- решать тригонометрические уравнения методом замены переменной, методом разложения на множители;
Однородные и линейные уравнения
Р/з «Тригонометрические уравнения, сводящиеся к алгебраическим»
97 - 98
Методы замены неизвестного и разложения на множители.
Простейшие тригонометрические уравнения, метод введения новой переменной, метод разложения на множители, однородные тригонометрические уравнения, алгоритм решения однородного уравнения второй степени
Уметь:
- решать тригонометрические уравнения методом замены переменной, методом разложения на множители;
Метод оценки левой и правой частей тригонометрического уравнения
99
Решение задач по теме: «Тригонометрические уравнения»
100
Контрольная работа №6 «Тригонометрические уравнения»
Глава X Повторение 5ч
101-105
Степенная функция
Логарифмическая функция
Показательная функция
Итоговая контрольная работа
Тригонометрические уравнения
содержание программы учебного курса
1.Степень с действительным показателем (13 ч.)
Действительные числа. Бесконечно убывающая геометрическая прогрессия. Арифметический корень натуральной степени. Степень с рациональным и действительным показателями.
Цель: формирование понятия степени с действительным показателем; выработка умения выполнять преобразования выражений, содержащих степень с действительным показателем.
2. Степенная функция (16 ч.).
Степенная функция, её свойства и график. Взаимно обратные функции. Сложные функции. Дробно-линейная функция. Равносильные уравнения и неравенства. Иррациональные уравнения. Иррациональные неравенства.
Цель: обобщение и систематизация знаний учащихся о степенной функции, а также знакомство с многообразием свойств и графиков степенной функции в зависимости от значений оснований и показателей степени, формирование умения решать простейшие иррациональные уравнения.
3. Показательная функция (15 ч.).
Показательная функция, её свойства и график. Показательные уравнения. Показательные неравенства. Системы показательных уравнений и неравенств.
Цель: знакомство с показательной функцией, её свойствами и графиком; формирование умения решать показательные уравнения и неравенства, системы, содержащие показательные уравнения.
4. Логарифмическая функция (20 ч.).
Логарифмы. Свойства логарифмов. Десятичные и натуральные логарифмы. Логарифмическая функция, её свойства и график. Логарифмические уравнения. Логарифмические неравенства.
Цель: знакомство с логарифмической функцией, её свойствами и графиком; формирование умения решать логарифмические уравнения и неравенства, системы, содержащие логарифмические уравнения.
5. Тригонометрические формулы (20 ч.).
Радианная мера угла. Поворот точки вокруг начала координат. Определение синуса, косинуса, тангенса угла. Знаки синуса, косинуса и тангенса. Зависимость между синусом, косинусом и тангенсом одного и того же угла. Тригонометрические тождества. Синус, косинус и тангенс углов α и -α. Формулы сложения. Синус, косинус и тангенс двойного угла. Синус, косинус и тангенс половинного угла. Формулы приведения. Сумма и разность синусов. Сумма и разность косинусов. Произведение синусов и косинусов.
Цель: формирование понятия синуса, косинуса, тангенса и котангенса произвольного угла (выраженного как в градусах, так и в радианах), знакомство с их свойствами и зависимостями, связывающими их, формирование умения применять формулы для преобразования простейших тригонометрических выражений.
6. Тригонометрические уравнения (16 ч.).
Уравнение cos x = 𝒶. Уравнение sin x = 𝒶. Уравнение tg x = 𝒶. Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения. Методы замены неизвестного и разложения на множители, метод оценки правой и левой частей тригонометрического уравнения
Тригонометрические уравнения различных видов. Системы тригонометрических уравнений. Тригонометрические неравенства.
Цель: формирование умения решать простейшие тригонометрические уравнения, знакомство с некоторыми приёмами решения тригонометрических уравнений.
СРЕДСТВА КОНТРОЛЯКонтрольная работа
Дата
1
Степень с действительным показателем
13
№ 1
2
Степенная функция
16
№ 2
3
Показательная функция
15
№ 3
4
Логарифмическая функция
20
№ 4
5
Тригонометрические формулы
20
№ 5
6
Тригонометрические уравнения
16
№ 6
7
Повторение
5
Итоговая
Всего
105
7
УЧЕБНО - МЕТОДИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ
-
Учебник: Алгебра и начала математического анализа, 10 класс. Ю.М.Колягин, М.В. Ткачева, Н.Е.Федорова, М.И.Шабунин, Просвещение,2009-2011г.
-
Алгебра и начала математического анализа. Дидактические материалы. М.И.Шабунин, М.В. Ткачева, Н.Е.Федорова, О.Н.Доброва. Просвещение, 2009 - 2011г.
-
Изучение алгебры и начал математического анализа. Книга для учителя. Н.Е.Федорова, М.В.Ткачева, Просвещение, 2011г.
-
Лысенко, Ф. Ф. Тематические тесты. Математика ЕГЭ -2015, 2016 / Ф. Ф. Лысенко. - Ростов н/Д.: Легион.
-
Таблицы по алгебре
-
Интернет - ресурсы:
- www. edu - "Российское образование" Федеральный портал.
- www. school.edu - "Российский общеобразовательный портал". -
www.school-collection.edu.ru/ Единая коллекция цифровых
образовательных ресурсов - www.mathvaz.ru - docье школьного учителя
математики
- www.it-n.ru "Сеть творческих учителей" - www
.festival.1september.ru</</u> Фестиваль педагогических
идей "Открытый урок"
Итоговая контрольная работа по алгебре и началам математического анализа
Итоговая контрольная работа по алгебре и началам математического анализа за курс 10 класса составлена в соответствии с учебником:
Алгебра и начала математического анализа: учебник для 10 класса общеобразовательных учреждений: базовый и профильный уровни /Ю.М.Колягин, М.В.Ткачёва и др./ под ред. А.Б. Жижченко - М.: Просвещение, 2009-2011.
Итоговая контрольная работа составлена с использованием заданий следующих пособий:
-
Самостоятельные и контрольные работы по алгебре и началам анализа для 10 - 11 кл. / А.П. Ершова, В.В. Голобородько. - М.: Илекса, 2012.
-
Математика. 10-й класс. Тесты для промежуточной аттестации и текущего контроля: учебно-методическое пособие. Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. / Ростов-на-Дону: Легион-М, 2016.
Цель работы: проверка уровня знаний, умений и навыков по ключевым темам курса алгебры 10 класса.
-
ВАРИАНТ 1.
Найдите значение выражения:
а)
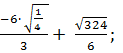 б)
б) 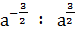 при а = 0,1 ;
при а = 0,1 ;
в)
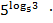
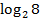 ; г) 2
; г) 2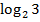 +
+ 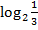 .
.
2. Найдите sin α, если cos α = - 0,6 и
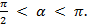
3. Вычислите: 2sin15˚۫∙cos15˚.
4. Решите уравнение:
а)
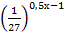 = 9 ; б)
= 9 ; б) 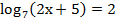 ;
;
в)
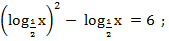 г)
г)  =
= 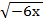 .
.
д) 2sin x - 1 = 0. Укажите наибольший отрицательный корень
в градусах.
-
Решите неравенство:
а) log3 (1 - x)
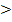 log3 (3 -
2x) ;
log3 (3 -
2x) ;
б)
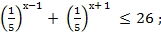
в)
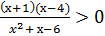
ВАРИАНТ 2.
-
Найдите значение выражения:
а)
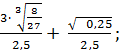 б)
б) 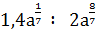 при а =
при а =  ;
;
в)
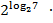
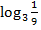 ; г)
; г) 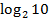 - 2
- 2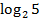 +
+ 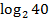 .
.
2. Найдите cos α, если sin α = 0,8 и
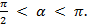
3. Вычислите: cos2 15˚ - sin2 15˚.
4. Решите уравнение:
а)
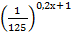 = 25 ; б)
= 25 ; б) 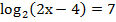 ;
;
в)
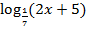
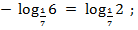 г)
г) 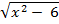 =
= 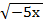 .
.
д) 2sin x + 1 = 0. Укажите ближайший к нулю корень в градусах.
5. Решите неравенство:
а)
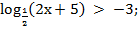
б)
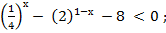
в)
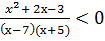 .
.
-