- Учителю
- Конспект уроков Числовая окружность на координатной плоскости
Конспект уроков Числовая окружность на координатной плоскости
Название предмета Алгебра и начала математического анализа
Класс 10
УМК Алгебра и начала математического анализа, 10-11 классы. В 2 . Ч.1. Учебник для общеобразовательных учреждений(базовый уровень) /А.Г. Мордкович. - 10-еизд., стер.- М.: Мнемозина,2012. Ч.2. Задачник для общеобразовательных учреждений(базовый уровень) /[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. - 10-еизд., стер.- М.: Мнемозина,2012.
Уровень обучения. Базовый
Тема урока Числовая окружность на координатной плоскости (3 часа)
Урок №1
Цели: ввести понятие модели числовой окружности в декартовой и криволинейной системе координат.
Задачи: формировать умение находить декартовы координаты точек числовой окружности и выполнять обратное действие: зная декартовы координаты точки, определять её числовое значение на числовой окружности.
Развивать вычислительные навыки, правильную математическую речь, логическое мышление учащихся.
Прививать самостоятельность, внимание и аккуратность. Воспитывать ответственное отношение к обучению.
Планируемые результаты:
Знать, понимать: - числовая окружность.
Уметь: - находить на окружности точки по заданным координатам; - находить координаты точки, расположенной на числовой окружности.
Уметь применять изученный теоретический материал при выполнении письменной работы.
Техническое обеспечение урока Компьютер, экран, проектор, учебник, задачник.
Дополнительное методическое и дидактическое обеспечение урока: Мордкович А. Г. М79 Алгебра и начала математического анализа. 10- 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. - М. : Мнемози- на, 2010. - 202 с. : ил
Ход урока
-
Организационный момент.
Психологический настрой учащихся.
Проверка домашнего задания 1. № 4.17 (в; г), № 4.18 (в; г), № 4.19 (в; г), № 4.20 (в; г).
Разобрать решение заданий вызвавших затруднение.
II. Устная работа.
(На слайде)
1. Назовите координаты точек плоскости:
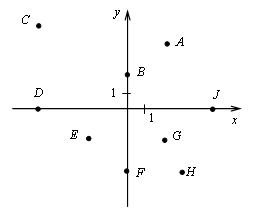
2. Назовите число, соответствующее заданной точке на числовой окружности.
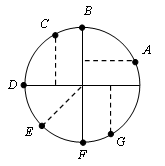
III. Объяснение нового материала.
1. Объяснение проводить согласно пункту учебника. Разместив числовую окружность в декартовой системе координат, следует подробно разобрать свойства точек числовой окружности, находящихся в различных координатных четвертях. Дело в том, что, изучая данную модель, учащиеся сталкиваются с определенными трудностями. Им необходимо учиться работать одновременно в двух системах координат - криволинейной и декартовой.
Для преодоления этой трудности авторы учебника применяют следующий методический прием: для точки М числовой окружности используют запись М(t), если речь идет о криволинейной координате точки М, или запись М (х; у), если речь идет о декартовых координатах точки.
(Мордкович А. Г. М79 Алгебра и начала математического анализа. 10- 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. - М. : Мнемози- на, 2010. - 202 с. : ил.)
2. Проводим 7-ю методическую «игру» - отыскание декартовых координат «хороших» точек числовой окружности. Речь идет о переходе от записи М(t) к М (х; у).
Можно организовать работу в парах с последующей самопроверкой (верные ответы в таблице 1 со с. 38 учебника).
3. Проводим 8-ю методическую «игру» - отыскание знаков координат «плохих» точек числовой окружности. Если, например, М(2) = М (х; у), то х 0; у 0. В процессе этой «игры» школьники фактически учатся определять знаки тригонометрических функций по четвертям числовой окружности.
Динамическая пауза
IV. Формирование умений и навыков.
1. № 5.1 (а; б), № 5.2 (а; б), № 5.3 (а; б).
Данная группа заданий направлена на формирование умения отыскивать декартовы координаты «хороших» точек на числовой окружности.
Решение:
№ 5.1 (а).
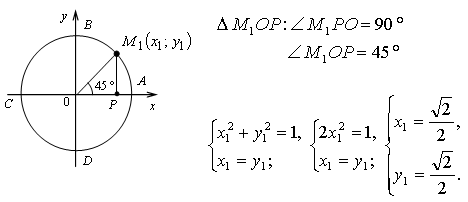
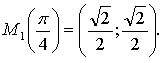
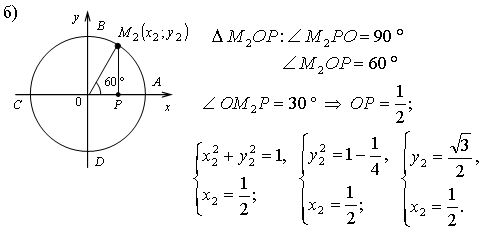
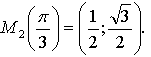
2. № 5.4 (а; б), № 5.5 (а; б).
Эта группа заданий направлена на формирование умений находить криволинейные координаты точки по её декартовым координатам.
Решение:
№ 5.5 (б).
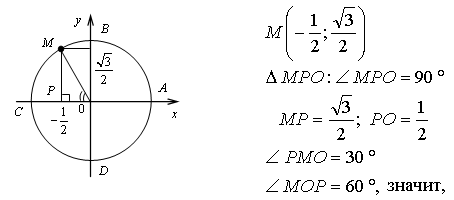
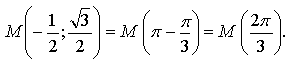
3. № 5.10 (а; б).
Данное упражнение направлено на формирование умения находить декартовы координаты «плохих» точек.
V. Итоги урока.
Вопросы учащимся:
- Что собой представляет модель - числовая окружность на координатной плоскости?
- Как, зная криволинейные координаты точки на числовой окружности, найти её декартовы координаты и наоборот?
Домашнее задание: , стр. 36. № 5.1 (в; г) - 5.5 (в; г), № 5.10 (в; г).
Урок №2
Цель: закрепить понятие модели числовой окружности в декартовой и криволинейной системе координат
Задачи: продолжить формирование умения переходить от криволинейных координат точки на числовой окружности к декартовым координатам; формировать умение отыскивать на числовой окружности точки, координаты которых удовлетворяют заданному уравнению или неравенству.
Развивать вычислительные навыки, правильную математическую речь, логическое мышление учащихся.
Прививать самостоятельность, внимание и аккуратность. Воспитывать ответственное отношение к обучению.
Планируемые результаты:
Знать, понимать: - числовая окружность.
Уметь: - находить на окружности точки по заданным координатам; - находить координаты точки, расположенной на числовой окружности.
Уметь применять изученный теоретический материал при выполнении письменной работы.
Техническое обеспечение урока Компьютер, экран, проектор, учебник, задачник.
Дополнительное методическое и дидактическое обеспечение урока: Мордкович А. Г. М79 Алгебра и начала математического анализа. 10- 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. - М. : Мнемози- на, 2010. - 202 с. : ил
Ход урока
-
Организационный момент.
-
Психологический настрой учащихся.
-
Проверка домашнего задания № 5.1 (в; г) - 5.5 (в; г), № 5.10 (в; г).
Разобрать решение заданий вызвавших затруднение.
-
Устная работа.
(на слайде)
1. Назовите криволинейные и декартовы координаты точек на числовой окружности.
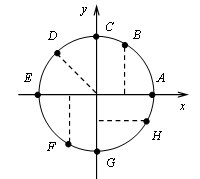
2. Сопоставьте дугу на окружности и её аналитическую запись.
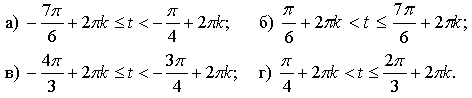
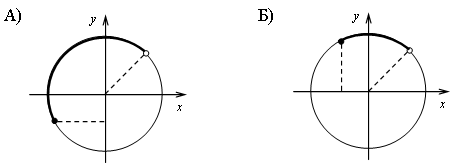
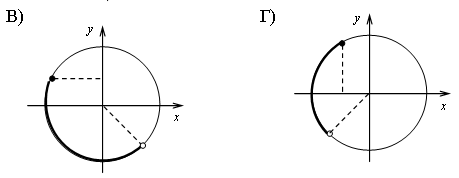
б
в
г
III. Объяснение нового материала.
1. На этом уроке учащиеся, по замыслу авторов учебника, отрабатывают две последние дидактические «игры», связанные с изучаемой моделью.
(Мордкович А. Г. М79 Алгебра и начала математического анализа. 10- 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. - М. : Мнемози- на, 2010. - 202 с. : ил.)
2. 9-я «игра» - отыскание на числовой окружности точек, координаты которых удовлетворяют заданному уравнению.
Рассматриваем примеры 2 и 3 со с. 41-42 учебника.
Важность этой «игры» очевидна: учащиеся
готовятся к решению простейших тригонометрических уравнений вида
![]() Для понимания сути дела следует прежде всего научить школьников
решать эти уравнения с помощью числовой окружности, не переходя к
готовым формулам.
Для понимания сути дела следует прежде всего научить школьников
решать эти уравнения с помощью числовой окружности, не переходя к
готовым формулам.
При рассмотрении примера на нахождение точки с
абсциссой ![]() обращаем внимание учащихся на возможность объединения ддвух серий
ответов в одну формулу:
обращаем внимание учащихся на возможность объединения ддвух серий
ответов в одну формулу:
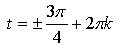
3. 10-я «игра» - отыскание на числовой окружности точек, координаты которых удовлетворяют заданному неравенству.
Рассматриваем примеры 4-7 со с. 43-44 учебника.
Решая подобные задачи, мы готовим учащихся к решению
тригонометрических неравенств вида ![]()
После рассмотрения примеров учащиеся могут самостоятельно сформулировать алгоритм решения неравенств указанного типа:
1) от аналитической модели 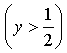 переходим к геометрической модели - дуга МР числовой окружности;
переходим к геометрической модели - дуга МР числовой окружности;
2) составляем ядро аналитической записи МР; для дуги получаем
![]()
3) составляем общую запись:
![]()
Динамическая пауза
IV. Формирование умений и навыков.
Работа в группах
1-я группа. Нахождение точки на числовой окружности с координатой, удовлетворяющей заданному уравнению.
№ 5.6 (а; б) - № 5.9 (а; б).
В процессе работы над этими упражнениями отрабатываем пошаговость выполнения: запись ядра точки, аналитической записи.
2-я группа. Нахождение точек на числовой окружности с координатой, удовлетворяющей заданному неравенству.
№ 5.11 (а; б) - 5.14 (а;б).
Главное умение, которое должны приобрести школьники при выполнении данных упражнений, - это составление ядра аналитической записи дуги.
V. Самостоятельная работа.
Вариант 1
1. Обозначьте на числовой окружности точку, которая соответствует заданному числу, и найдите её декартовы координаты:
![]()
2. Найдите на числовой окружности точки с данной
абсциссой ![]() и
запишите, каким числам t они соответствуют.
и
запишите, каким числам t они соответствуют.
3. Обозначьте на числовой окружности точки с
ординатой, удовлетворяющей неравенству ![]() и
запишите при помощи двойного неравенства, каким числам t они
соответствуют.
и
запишите при помощи двойного неравенства, каким числам t они
соответствуют.
Вариант 2
1. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты:
![]()
2. Найдите на числовой окружности точки с данной ординатой у = 0,5 и запишите, каким числам t они соответствуют.
3. Обозначьте на числовой окружности точки с
абсциссой, удовлетворяющей неравенству 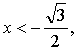 и
запишите при помощи двойного неравенства, каким числам t они
соответствуют.
и
запишите при помощи двойного неравенства, каким числам t они
соответствуют.
VI. Итоги урока.
Вопросы учащимся:
- Как найти на окружности точку, абсцисса которой удовлетворяет заданному уравнению?
- Как найти на окружности точку, ордината которой удовлетворяет заданному уравнению?
- Назовите алгоритм решения неравенств с помощью числовой окружности.
Домашнее задание: , стр. 36. № 5.6 (в; г) - № 5.9 (в; г),
№ 5.11 (в; г) - № 5.14 (в; г).
Урок №3
Цели: ввести понятие модели числовой окружности в декартовой и криволинейной системе координат.
Задачи: проверить степень усвоения ранее изученного материала,
актуализировать знания учащихся, необходимые при изучении новой темы.
Развивать вычислительные навыки, правильную математическую речь, логическое мышление учащихся.
Прививать самостоятельность, внимание и аккуратность. Воспитывать ответственное отношение к обучению.
Планируемые результаты:
Знать, понимать: - числовая окружность.
Уметь: - находить на окружности точки по заданным координатам; - находить координаты точки, расположенной на числовой окружности.
Уметь применять изученный теоретический материал при выполнении письменной работы.
Техническое обеспечение урока Компьютер, экран, проектор, учебник, задачник.
Дополнительное методическое и дидактическое обеспечение урока: Мордкович А. Г. М79 Алгебра и начала математического анализа. 10- 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. - М. : Мнемози- на, 2010. - 202 с. : ил
Ход урока
-
Организационный момент.
-
Приветствие учеников, поверка отсутствующих Психологический настрой учащихся.
-
Проверка домашнего задания № 5.6 (в; г) - № 5.9 (в; г), № 5.11 (в; г) - № 5.14 (в; г).
Разобрать решение заданий вызвавших затруднение.
II. Фронтальный опрос по теме:
-
Дайте определение числовой окружности
-
Сколько четвертей имеем в единичной окружности?
Как они называются? -
Определите знаки в каждой из четверти.
-
Проверочная работа
После выполнения заданий, учащиеся сдают листочки, а затем вместе с учителем проверяют правильные ответы.2
Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству .
3
Найдите множество чисел, которым соответствуют отмеченные на числовой окружности точки
Вариант №2
1
Найдите на числовой окружности точки, которые соответствуют данным числам: .
2
Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству .
3
Найдите множество чисел, которым соответствуют отмеченные на числовой окружности точки
Вариант №3
1
Найдите на числовой окружности точки, которые соответствуют данным числам: .
2
Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству .
3
Найдите множество чисел, которым соответствуют отмеченные на числовой окружности точки
Вариант №4
1
Найдите на числовой окружности точки, которые соответствуют данным числам: .
2
Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству .
3
Найдите множество чисел, которым соответствуют отмеченные на числовой окружности точки
Динамическая пауза
IV. Обобщение материала
1. Рассмотреть числовую окружность в декартовой системе координат.
2. Составить таблицу координат чисел числовой окружности для первого макета.
3. Составить таблицу координат чисел числовой окружности для второго макета.
У каждого из вас в тетради есть три макета числовой окружности. Каждая точка числовой окружности имеет в координатной плоскости свои координаты. Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.
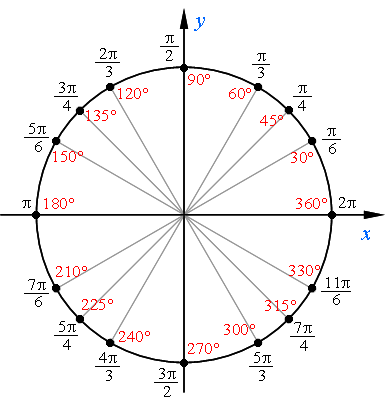
На первом макете возьмем точку M(π/4) середина I четверти. Опустим перпендикуляр MP на прямую OA и рассмотрим треугольник OMP. Так как дуга AM составляет половину дуги AB, то ∡MOP=45°. Значит, треугольник OMP - равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x=y. Так как координаты точки M(x;y) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений:
Подставив x вместо y в первое уравнение системы, получим следующее решение:
При решении учитываем, что абсцисса точки M положительна.
Получили, что координаты точки M, соответствующей числу π/4 будут M(π/4)=M(2√2;2√2)
Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу:
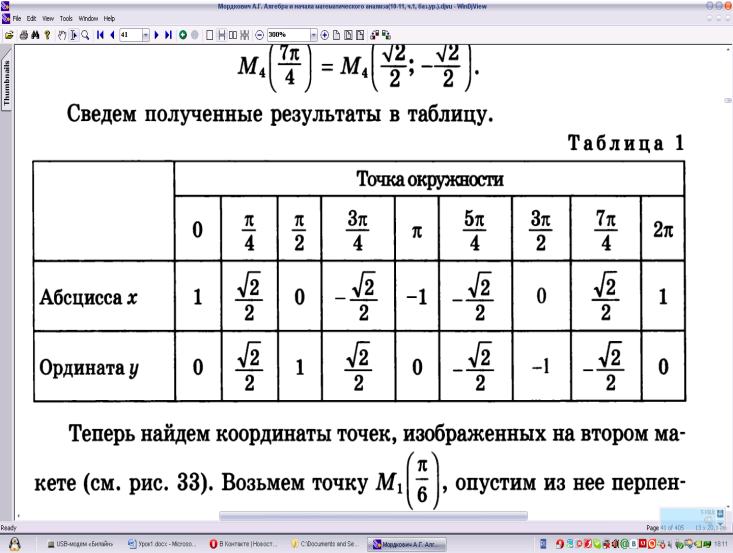
Перейдем на второй макет. Рассуждаем аналогично для точки M, если теперь она соответствует числу π/6
Треугольник MOP прямоугольный. Так как дуга AM составляет третью часть дуги AB, то ∡MOP=30°.
Катет MP лежит против угла 30 градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т.е. ордината точки M равна
MP=1/2 y=1/2
Абсциссу x точки M найдём, решив уравнение:
При решении учитываем, что абсцисса точки M положительна.
Получили, что координаты точки M, соответствующей числу π/6 будут M(π/6)=M(3√2;1/2)
Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.
На третьем макете возьмем угол в 600 или π/3. Треугольник OKF прямоугольный. Так как дуга AK составляет третью часть дуги AB, то ∡KOF=60°, а ∡OKF=30°,
Катет OF лежит против угла 30 градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т.е. абсцисса точки F равна
OF=1/2 x=1/2
Ординату y точки K найдём, решив уравнение:
При решении учитываем, что ордината точки K положительна.
Получили, что координаты точки K, соответствующей числу π/3 будут K(π/3)=F(1/2, 3√2) . Полученные данные занесем в таблицу:
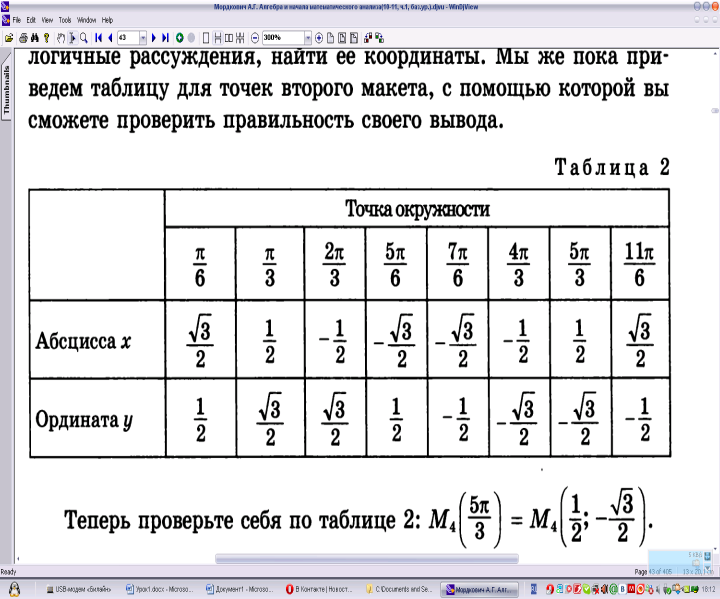
V. Подведение итогов урока, постановка домашнего задания, рефлексия.
Понятие числовой окружности вы изучали для того чтобы перейти к изучению таких важных с точки зрения математики и геометрии понятий как синус, косинус, тангенс и котангенс.
Вопросы учащимся:
Итак, что мы сегодня узнали на уроке нового?
Домашнее задание: , стр. 36. № 5.8, № 5.13 (в,г)