Учителю
Проект урока по теории вероятностей в 9 классе Тема урока: «Комбинаторные методы решения вероятностных задач»

Проект урока по теории вероятностей в 9 классе Тема урока: «Комбинаторные методы решения вероятностных задач»

Автор публикации: Шакирова А.С.

Дата публикации: 24.12.2014

Краткое описание: Данный урок соответствует программе по элективному курсу и служит в помощь учителям математики в старших классах. Целью данного урока является: Выработать умение распознавать основные типы вероятностных задач, решаемых комбинаторными методами.ЗАДАЧИ:образовательны

предварительный просмотр материала

МБОУ Моховская основная общеобразовательная школа
Чановского района Новосибирской области

Проект урока по теории вероятностей в 9 классе

Тема урока: «Комбинаторные методы решения
вероятностных задач»

Составила: Шакирова А.С.

Образование: высшее, 2006г, НГПУ

Стаж: 8 лет

Введение.

Современная школа живет в условиях реформ. Обозначены основные направления развития российского образования: совершенствование программ и стандартов; поддержка инноваций в системе образования и др. Вовремя в школьной программе появляется курс «Элементы комбинаторики, статистики и теории вероятностей». При проведении уроков по этому курсу учитель имеет возможность формировать устойчивый интерес к изучению математики, развивать интеллект воспитанников, способность ориентироваться в окружающей действительности, строить прогнозы. Этот курс знакомит учащихся со случайными величинами, они необычны для школьников и для учителей, но естественны в повседневной жизни. Многие законы природы и общества имеют вероятностный характер, реальные явления и процессы часто описываются вероятностными моделями.

В последние годы произошли положительные сдвиги к внедрению вероятностно-статистической линии в содержание школьного образования. В действующие учебники для 7-9 классов включена тема «Элементы статистики, комбинаторики и теории вероятности».

Естественные, гуманитарные и технические науки во многом используют теоретико-вероятностные методы. Стохастические модели более полно отражают реальные объекты и явления, чем детерминистские.

Но не только в науке, во многих сферах человеческой деятельности (промышленное производство, сельское хозяйство, транспорт, связь, военное дело, здравоохранение и т. д.) мы постоянно сталкиваемся со стохастическими процессами и явлениями, с необходимостью учитывать статистические закономерности и использовать их. Известны примеры, когда игнорирование стохастического характера явления оборачивается колоссальными материальными потерями - в энергосбережении, на транспорте, в других сферах народного хозяйства.

Если говорить, например, о промышленном производстве, то следует иметь в виду его характерную черту - контроль качества продукции. Идея статистического приемочного контроля возникла в связи с большой трудоемкостью сплошного контроля качества продукции, при котором на некоторых предприятиях следовало бы иметь по 2-3 контролера на каждого рабочего. Кроме того, эти методы во многих случаях приходится использовать и по другой причине: иногда испытание качества изделий приводят к их гибели или такой порче, что дальнейшее использование становиться невозможным. Полностью исключить ошибки при статистическом контроле , как известно, нельзя. Поэтому тем более важно так организовать процедуру проверки, чтобы снизить до минимум вероятность ошибок: приемки недоброкачественной партии или отклонении доброкачественной. Для этого необходимы теоретико-вероятностные познания, причем не только у работников высшей квалификации, организующих производственный процесс. Но и у работников, непосредственно осуществляющих проверку.

Правильный учет и использование статистических закономерностей в науке и практике требуют мышления особого склада - статистического. Статистическое воспитание должно начинаться со школы и осуществляться не только на уроках математики, но и ряда других предметов. Межпредметные связи между математикой и физикой, математикой и биологией и т.д., основанные на статистическом подходе, оказываются двусторонними. Физики, биология, химия изобилуют примерами случайных явлений - эти дисциплины не могут обойтись без элементов теории вероятностей для раскрытия собственных закономерностей. Например, учение Дарвина или молекулярная физики. Теоретико-вероятностные знания вовлекают в сферу межпредметных связей целый комплекс дисциплин. Уместно подчеркнуть их единую основу - вероятностный характер. Целесообразно провести параллель между ролью флуктуации в тепловых явлениях и в химических реакциях. Таким образом, представляется возможным раскрыть взаимосвязи различных форм движения материи, выявить многочисленные и глубокие связи между различными на первый взгляд задачами, создать перед мысленным взором учащихся единую картину мира.

Использование межпредметных связей, с одной стороны, обогащает теоретико-вероятностную подготовку учащихся примерами прикладного содержания, с другой стороны, оно способствует более глубокому усвоению других предметов.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Данный урок соответствует программе по элективному курсу и служит в помощь учителям математики в старших классах.

Целью данного урока является: Выработать умение распознавать основные
типы вероятностных задач, решаемых
комбинаторными методами.

ЗАДАЧИ:

образовательные

обобщить и систематизировать знания по теме «Элементы комбинаторики
и теории вероятностей»
подготовиться к контрольной работе
овладение конкретными математическими знаниями, необходимых для
применения в практической деятельности, в жизненной ситуации;

развивающие

развитие математического мышления, развитие умения сравнивать,
обобщать, выявлять закономерности;

воспитательные

воспитание чувства ответственности, такие качества личности, как
познавательная активность, самостоятельность, упорство в достижении
цели.

При проведении этого урока я использовала различные формы и методы:

индивидуальная работа;
фронтальная работа;
коллективная работа;
самостоятельная работа (тест);
применение ИКТ.

На данном уроке я предусмотрела применение 4-х технологий:

проблемно-диалогического обучения при постановке проблемы: «Выбрать алгоритм решения задачи № 13 из Демо-версии ГИА»;
оценивание учебных успехов при развитии у ученика самостоятельно оценивать результат, контролировать самого себя и исправлять собственные ошибки (при выполнении различных заданий);
формирование типа правильной читательской деятельности (при чтении текста задачи, заданий самостоятельной работы);
Проектная (на стенде формирует опорный конспект).

В результате изучения этой темы учащиеся должны

знать:

основные понятия;
формулы комбинаторики, формулы различных подходов к определению вероятности.

уметь:

распознавать основные типы вероятностных задач;
применять комбинаторные методы решения вероятностных задач.

ТЕМА: Комбинаторные методы решения вероятностных задач

ДИДАКТИЧЕСКАЯ ЦЕЛЬ УРОКА.

Выработать умение распознавать основные типы вероятностных задач, решаемых комбинаторными методами.

ЗАДАЧИ:

образовательные

развивающие

развитие математического мышления, развитие умения сравнивать,
обобщать, выявлять закономерности;

воспитательные

ОБОРУДОВАНИЕ:

презентации Microsoft Office Power Point 2003 «Комбинаторные методы решения вероятностных задач».
Индивидуальная карта учета контроля.
Карточка с буквами: - достоверное (Д), - невозможное (Н), - случайное (С), - совместное (С), - несовместные (Н).
Интерактивный тест.

ХОД УРОКА

«Теория вероятностей есть, в сущности, не то иное, как здравый смысл, сведенной к исчислению». Лаплас

Организационный момент.

Здравствуйте, ребята. Садитесь на свои
места поудобнее, прислушайтесь к своему
дыханию. Сегодня у нас в гостях учителя
преподающие математику в 9 классах со
всех школ Чановского района.

Повторение и систематизация знаний.

Сегодня утром я решила позвонить на метеостанцию, чтобы выяснить температуру, но не смогла вспомнить последовательность трех последних цифр. Помня лишь, что это цифры 3,7и 9, я набрала первые две цифры, которые я знала и наугад комбинацию из цифр 3,7,9.
Какова вероятность того, что я набрала верный номер?

Сколько человек я разбудила, если только последний звонок был удачным?

Р(А)=Р3=3!= 3·2·1=6

Конечно это шутка!

Скажите, пожалуйста, знания, каких предметов вам понадобились для ответа на мои вопросы?

- Дайте определение данным предметам.

(Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Теория вероятностей - раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними).

(Комбинаторика и теория вероятностей)

Постановка проблемы.

В настоящее время Теория вероятностей имеет статус точной науки наравне с арифметикой, алгеброй, геометрией, тригонометрии и т.д. Этот раздел математики уже входит в школьные учебники и в этом году включен в программу государственной аттестации (ГИА).

- Ребята, скажите, пожалуйста, в какой части ГИА, ваших демо-версиях ГИА по математике в этом учебном году, со структурой которого вы уже знакомы, находятся задания по теории вероятности и математической статистике? (в первой части).

- Прочтите задание под № 13 и № 14, скажите, что мы должны знать для решения задач такого типа? (классическое определение вероятности и её формулу для №13, а для №14 пригодятся знания математической статистики).

Значит для того, чтобы удачно сдать ГИА по математике, нужно хорошо знать, на ряду с изученными темами:

- Числа и вычисления,

- Алгебраические выражения,

- Уравнения и неравенства,

- Числовые последовательности,

- Функции и графики,

- Координаты на прямой и плоскости,

Геометрия, необходимы знания и Статистики и теории вероятностей.

Слайд 1.

И поэтому тема нашего сегодняшнего урока «Комбинаторные методы решения вероятностных задач».

Для того чтобы решать вероятностные задачи комбинаторными методами нужно выработать умение:

Распознавать основные типы вероятностных задач;
Знать комбинаторные методы решения вероятностных задач.

И поставим проблему сегодняшнего урока Выработать алгоритм решения задачи №13 из Демо-версии ГИА

Слайд 2.

Для того чтобы решить эту проблему, мы должны обобщить и систематизировать знания по курсу «Статистика и теория вероятностей».

На уроке мы будем выполнять разные виды работ, а т.к. любая работа оценивается на ваших оценочных листах вы будете заносить оценки за проделанную работу. (приложение 1)

Оценочный лист
по теме «Комбинаторные методы решения
вероятностных задач»

Ученика 9 класса _____________________________________

1этап «Теория» - я знаю все
определения и формулы.

2 этап «Устная работа» - быстро
решаю задачи устно.

3 этап «Тест».

4 этап «Вычисли» - знаю все
формулы и умею применять

5 этап «Решение задач» - знаю все
формулы и умею применять
для решения задач

«5» - я знаю, я умею применять все

«4 » - я знаю все, но затрудняюсь
применять

«3» - я знаю не все и затрудняюсь
применять

«2» - я не знаю, не умею
применять

«Теория»

«Устная работа»

«Тест»

«Вычисли»

«Решение задач»

Итого

III.Давайте вспомним основные понятия, как ручеек течет быстро, так и мы быстро ответим на вопросы (мя - передают друг другу).

Слайд 3.

Слайд 4.

IV.Устное решение задач.

Сегодня на уроке мы и рассмотрим некоторые задачи, которые решаются по правилам комбинаторики и теории вероятностей.

Задание №1.

Наугад называется натуральное число от 1 до 30. Какова вероятность того, что это число:

6;
не 6;
кратно 6;
не кратно 5;
простое число;
квадратное число;
не меньше 27?

Решение.

n =30/

m=1.P(A)=1/30.
m=m-1. m=29. P(B)=29/30.
m=5. (6; 12; 18; 24; 30). Р(С)=5/30=1/6.
m=30-6=24. Р(Д)=24/30=4/5.
m=10. (2,3,5,7,11,13,17,19,23,29).
Р(Е)=10/30=1/3.
m=5. (1,4,9,16,25). P(F) =5/30=1/6.
m=4/ (27,28,29,30). P(H)=4/30=2/15.

Задание №2(с карточками)

Учащимся читается условие задачи, у каждого в руках карточки с буквами.

1) С помощью карточек покажите, какое это событие - достоверное (Д), невозможное (Н), случайное (С).

а) Вы открыли книгу на любой странице и прочитали первое попавшееся существительное. Оказалось, что:

- в написании выбранного слова есть гласная буква. (Д).

- в написании выбранного слова есть буква «о». (С).

- в написании выбранного слова нет гласных букв. (Н),

- в написании выбранного слова есть мягкий знак. (С).

- слово начинается с «ъ». (Н).

2) с помощью карточек покажите , какие пары событий являются:

совместными (С) и несовместными (Н).

а) брошена игральная кость; на верхней грани оказалось:

- 6 очков; 5 очков; (Н).

- 6 очков; четное число очков; (С).

б) из полной колоды карт вынимается одна карта:

- «вынута карта красной масти» и «вынут валет»; (С).

- «вынут король» и «вынут туз»; (Н).

в) у случайным образом составленного квадратного уравнения, есть действительные корни;

- дискриминант уравнения отрицателен; (Н).

достоверное (Д)

случайное (С)

невозможное (Н)

случайное (С)

невозможное (Н)

несовместными (Н)

совместными (С)

несовместными (Н)

V. Самостоятельная работа (интерактивный тест на компьютерах)

(7 мин.)

Вариант 1

Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?

30 2) 100 3) 120 4) 5.

В 9 «Б» классе 32 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

128 2) 35960 3) 36 4) 46788.

Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

10 2) 60 3) 20 4) 30.

Вычислить: 6! - 5!

600 2) 300 3) 1 4) 1000.

Вариант 2.

Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?

100 2) 30 3) 5 4) 120.

Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?

3 2) 6 3) 2 4) 1.

Сколькими способами из 9 учебных предметов можно составить расписание учебного дня из 6 различных уроков.

10000 2) 60480 3) 56 4) 39450.

Вычислите:

2 2) 56 3) 30 4) .

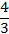Вариант 3.

Сколькими способами можно расставить 4 различные книги на книжной полке?

24 2) 4 3) 16 4) 20.

Сколько диагоналей имеет выпуклый семиугольник?

30 2) 21 3) 14 4) 7.

В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?

22 2) 11 3) 150 4) 110.

Сократите дробь:

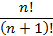
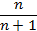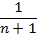1 2) 3) 4)

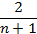
Вариант 4.

Сколькими способами могут встать в очередь в билетную кассу 5 человек?

5 2) 120 3) 25 4) 100.

Сколькими способами из 25 учеников класса можно выбрать четырех для участия в праздничном концерте?

12650 2) 100 3) 75 4) 10000.

Сколько существует трехзначных чисел, все цифры которых нечетные и различные.

120 2) 30 3) 50 4) 60.

Упростите выражение:

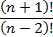
0,5 2) 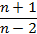3) 4)

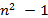
0 ошибок - «5».

1 ошибка - «4».

2 ошибки - «3».

больше 2 ошибок - «2».

VI. Решение задач.

Вычислить (на карточках по 2 задания) у доски:

8! - 6!

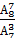
Решим задачу №13 из Демо-версии ГИА - 2012 года по математике. (решение по классическому определению вероятности)

Дополнительные задачи

1.З а д а ч а. Из 12 девушек и 10 юношей выбирают команду, состоящую из 5 человек. Сколькими способами можно выбрать эту команду, чтобы в нее вошло не более трех юношей?

2.З а д а ч а. При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов.

Слайд 5.

Слайд 6.

VII.Итог урока.

Итак, сегодня на уроке мы вспомнили основные понятия, формулы комбинаторики и теории вероятности, рассмотрена нахождение вероятности, увидели связь между комбинаторикой и теорией вероятностей.

VIII.Домашнее задание. (На карточках).

В отдел уголовного розыска поступило сообщение о том, что 5 неизвестных лиц взломали сейф и похитили крупную сумму денег. Свидетели успели заметить, что грабители сели в автобус, следующий по маршруту в соседний город. Об этом сразу же была поставлена в известность милиция. Как только автобус остановился на автовокзале, к его дверям подошел инспектор уголовного розыска и запретил кондуктору открывать дверь автобуса. Тот сообщил инспектору, что в автобусе 40 пассажиров. Обыск может привести к значительной задержке автобуса. Инспектор успокоил кондуктора: «Мне достаточно проверить человек 6 пассажиров и сможете ехать дальше!». Он предложил шестерым, наугад выбранным пассажирам, зайти в кабинет начальника вокзала. Один преступник был сразу обнаружен - в его кармане нашли пачку денег. Он назвал сообщников и дело было закончено. Что руководило инспектором: РИСК или ТРЕЗВЫЙ РАСЧЕТ? (приложение 2.)

Приложение 1.