Урок на тему Логарифмические уравнения

Государственное бюджетное профессиональное общеобразовательное учреждение

«Невинномысский энергетический техникум»

Методическая разработка открытого занятия по дисциплине «Математика»

Тема занятия:

^{Логарифмические уравнения}

Преподаватель математики:

Скрыльникова Валентина Евгеньевна

Невинномысск 2016 год.

Цели:

Обучающие:

1.Научиться решать логарифмические уравнения, используя методы решения логарифмических уравнений, определение и свойства логарифмов.

Развивающие:

1.Развитие операций мышления (обобщения, анализа, выделения главного).

2.Развитие культуры математической речи, интереса и внимания.

3. Развитие навыков сотрудничества.

Воспитательные:

1.Воспитание сознательного отношения к изучению математики.

2.Воспитание стремления к самосовершенствованию.

3.Предоставить каждому учащемуся возможность проверить свои знания и

повысить их уровень .

Тип урока: урок изучения нового материала.

Методы и приёмы: словесный и наглядный.

Форма работы: индивидуальная, групповая, коллективная, устная, письменная.

Наглядность к уроку и раздаточный материал: компьютер, мультимедийный

проектор, экран, магнитная доска, карточки для проведения самостоятельной

работы, презентация слайдов, учебник «Алгебра и начала анализа 10-11 класс».

Задачи урока: Ранее усвоенные знания применять в нестандартных ситуациях.

Ход урока

1. Организация на урок /5 минут/.

2. Повторение теоретического материала по теме " Равносильные уравнения. Решение логарифмических уравнений":
   
   а) устная работа (просмотр презентаций, обсуждение теоретических вопросов) / 10минут/;
   
   б) диктант с последующей проверкой /10минут/.

3. Работа учащихся с карточками (нахождение ошибок) (самостоятельно), обсуждение решений уравнений /15 минут/.

4. Совместная работа учащихся и учителя (решение уравнений в тетрадях и у доски) /30минут/.

5. Подготовка к экзаменам:
   
   а) разбор уравнений, решения которых заранее подготовлены учителем для просмотра через плазменный экран и решаемого учеником /10 минут/;
   
   б) самостоятельная работа учащихся (по карточкам разного уровня сложности) /20минут/.

6. Итог урока, выставление оценок /5 минуты/.

I. Организационный момент. (Приветствие)

Вступительное слово преподавателя.

Я приветствую вас на сегодняшнем уроке алгебры. Тема урока: "Решение логарифмических уравнений". Сегодня мы повторим понятие логарифма числа, свойства логарифма, закрепим умения применять эти понятия при решении уравнений.

Эпиграфом урока являются слова:

Скажи мне - и я забуду,

Покажи мне - и я запомню,

Дай мне действовать самому - и я научусь.

Древнекитайская мудрость

II. Повторение теоретического материала по теме: " Равносильные уравнения. Решение логарифмических уравнений"

Для того, чтобы решать логарифмические уравнения, следует повторить необходимые для этого теоретические сведения:

Теоретическая разминка:

Попытайтесь восстановить или дополнить недостающие элементы в

данных равенствах ( Пользуясь карточками с элементами и магнитами на

магнитной доске ):

-определение логарифма?(Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести основание a, чтобы получить число b)

-основное логарифмическое тождество?(b=b)

-чему равен логарифм произведения? (xy=x+y)

-чему равен логарифм частного? (=x-y)

-чему равен логарифм числа по этому же основанию? (1)

-чему равен логарифм единицы по любому основанию? (0)

-при возведении в степень логарифм?(=px

-формула перехода от одного основания логарифма к другому? x=)

-что значит решить уравнение?(найти все значения переменной, при которых

уравнение обращается в верное числовое равенство или доказать, что таких

значений нет.)

-что такое корень уравнения? ( значение переменной, при которой уравнение

обращается в верное числовое равенство)

-давайте вместе сформулируем, какие же уравнения называются

логарифмическими? (-уравнения, в которых переменная содержится под знаком

логарифма, называют логарифмическими).

2.Используя свойства и определение логарифма вычислите и выберите правильный ответ - устно (слайд)

log3√3 () 2 (7, 5, 8)

(2, 4, 1) (0, 2, 1)

(1, 2, 0) (4, 2, 1)

Правильные ответы:

3 8

4 1

0 4

Диктант (с последующей взаимопроверкой)

Возможные ответы: "+"-да , "-" - нет

Устная работа.

1. Укажите промежуток, которому принадлежит больший корень уравнения ln(х - 5)² = 0.

1) (-7;-5);

2)(-5;-3);

3)(2;4);

4) (5; 7).

2. Найдите произведение корней уравнения 1- lg(x² +1) = 0.

1)-99;

2)-9;

3)33;

4)-33.

3. Укажите промежуток, которому принадлежат корни уравнения log₀,₅(x - 9) = 1 + log₀,₅5.

1) (11; 13);

2) (9; 11);

3) (-12;-10);

4) [-10;-9].

4. Укажите промежуток, которому принадлежит корень уравнения log4(x - 5) = log₂₅5.

1)(-4;-2);

2) (6; 8);

3) (3; 6);

4) (-8; -6).

Ответы:

1

2

3

4

Номер ответа

4

2

1

2

-Существует несколько методов решения логарифмических уравнений, мы сегодня

познакомимся c тремя методами.

- по определению

-метод потенцирования

- введения новой переменной

Давайте решим эти уравнения вместе, используя план и методы решения:

Пример №1 показывает у доски преподаватель:

-по определению логарифма решаем

ОДЗ:8х-4>0 х>

8х-4=

8х=4+4

8х=8

Х=1

Ответ: х=1

№2.Второй пример делает обучающийся у доски:

Давайте сформулируем алгоритм решения уравнения и запишем в блокнот:

1.Записать условия, задающие ОДЗ.

2.Выбрать метод решения.

3.Решить уравнение.

4.Проверить получившиеся корни, подставив их в условия ОДЗ.

5.При записи ответа, исключить посторонние корни.

Решить уравнения, используя план и методы решения.

Пример №3,показывает решение преподаватель

-методом потенцирования,

ОДЗ:

данное уравнение будет равно уравнению вида

3х-6=4х-10

3х-4х=6-10

-х=-4

Х=4

Ответ : х=4

Пример №4,делает обучающийся у доски:(14-4x)=(2x+2)

Пример № 5 показывает преподаватель у доски:

- методом введения новой переменной

ОДЗ: х>0

Пусть =t, тогда уравнение примет вид

=0 - решаем квадратное уравнение, находим дискриминант

=16-12=4

Находим корни уравнения:

=(-b+)/2a=4+2/2=3

=(b-)/2a=4-2/2=1

вращаемся к нашей подстановке:=t,=3,х=

=,=2

Ответ:х=8,х=2.

Пример № 6 ,делает обучающийся у доски:

III. Работа учащихся с карточками. Объяснение ошибок

Учащимся на отдельных листах предлагаются уравнения с решениями, содержащими ошибки. Необходимо обнаружить эти ошибки, объяснить их и выполнить решение предложенных уравнений правильно (допускается решение уравнения иным способом после обнаружения ошибки в приведенном варианте решения).

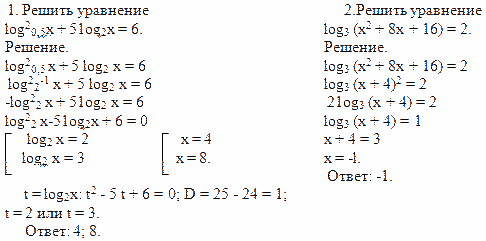
Вариант 1

1. Решите уравнение log₃(x+2)=3

1) 29;

2) 7;

3) 25;

4) 11

2. Укажите промежуток, которому принадлежит корень уравнения log₁₂(x+3)= log₁₂(6-5x)

1) (1,2;3);

2) (0,1);

3) (-3;0);

4) (1;1,2)

3. Найдите сумму корней уравнения - 5log₄x+2=0

1) 2,5;

2) 18;

3) 14;

4) 1,5

4. Решите уравнение log₁₆x+ log₄x+ log₂х=7

Часть 3

5. Найдите произведение корней уравнения

Вариант 2

1.Решите уравнение log₁₁(2x+1)=2

1) 2;

2) 11;

3) 60;

4) 5

2. Укажите промежуток, которому принадлежит корень уравнения -log₅(4-х)= log₁₅2-1

1) (0;4);

2) (-6,-4);

3) (-4;0);

4) (4;10)

3. Найдите сумму корней уравнения

1) 27;

2) ;

3) ;

4)

4. Напишите целые корни уравнения+7=2,5

Решите уравнение 3(3-)=(2+)+3

Вариант 3

1. Решите уравнение log_0,5(2x-0,75)=2

1) 4;

2) 2;

3) 0,5;

4) 1

2. Укажите промежуток, которому принадлежит корень уравнения

log₄3+ log₄(3-х)= 1+log₄(1-2х)

1) (-4;2); 2) (-2, 0); 3) (0;0,5); 4) (0,5;4)

3. Решите уравнение log₃х+14-32=0 (Если уравнение имеет более одного корня, то в бланке ответов запишите произведение всех его корней)

4. Найдите наибольший корень уравнения log₃¦х+2¦+9= log₃(х+2)⁴

5. Решите уравнение

Ответы:

1

2

3

4

5

Вариант 1

3

1

2

16

1

Вариант 2

3

1

2

49

-2

Вариант 3

4

2

81

25

-1

Проверка выполнения тестов на оценку. Анализ выполнения тестов.

V .Подведение итогов урока, выставление оценок:

Сегодня на уроке ребята, мы:

- повторили определение и свойства логарифмов,

- рассмотрели 3 метода решения логарифмических уравнений,

- составили алгоритм решения уравнений,

- используя эти знания, научились решать логарифмические уравнения.

Итог урока:

Пренебрегать теорией нельзя, в этом мы с вами убедились на уроке: без знания теоретического материала невозможно уверенно решать практические задания.

Домашнее задание

Решите уравнение (1-6).

1. + = 3.

2. log₃ х² + log₂ (2 - х) = log₂ (4 - 4х).

3. log₂ (x² + 10х + 25) = 2.

4.=0,5

5. log₃ (x + 1) + log₃ (x - 2) = log₃ (x + 6).

6. |log₂x - 1 |=(2х + 5) (log₂x - 1)