Урок математики в 5 классе «Сравнение отрезков. Длина отрезка»

Урок математики в 5 классе «Сравнение отрезков. Длина отрезка»

Учитель: Кабанова Светлана Александровна,

Тобольский район, Филиал «МАОУ Нижнеаремзянская СОШ» - «МАОУ Малозоркальцевская СОШ»

1. Образовательные:

• повторить определение середины отрезка, изображение и обозначение луча, отрезка, прямой, взаимное расположение прямых, лучей, отрезков;

• совершенствовать навыки решать задачи на нахождение длины отрезка;

• продолжить дальнейшую работу по выработке умения находить сходства и различия.

2. Развивающие:

• развивать умения наблюдать, подмечать закономерности;

• проводить рассуждения по аналогии;

• анализу и самоанализу;

• активности, принимать самостоятельные решения.

3. Воспитательные:

• содействовать воспитанию интереса к математике,

• способствовать расширению общекультурного кругозора;

• способность к эффективному общению, толерантности.

Оборудование: экран, компьютер, мультимедийный проектор (или интерактивная доска), презентация к уроку.

Тип урока: комбинированный в технологии ИКТ.

Методы обучения: словесный, визуальный, интерактивный, с элементами технологии дифференцированного обучения учащихся.

Эпиграф к уроку:

"Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!»

Д. Пойа

Ход урока:II. Проверка домашней работы.

Перед уроком необходимо сфотографировать домашнюю работу хорошоуспевающего ученика и вставить в слайд.

На уроке разобрать домашние задания.

слайд 2

3-4 мин

1 отметка

III. Постановка целей урока.

Вместе с учениками, опираясь на тему урока, ставим цели.

слайд 3

1-2 мин

IV. Актуализация знаний.

1. Индивидуальная работа:

Трое успешных учащихся решают задачи по индивидуальным карточкам и сдают работу на проверку, после чего присоединяются к классу.

Карточки см.приложение №1;

8 - 10 мин.

2-4 отметки

2. Фронтальный опрос.

Остальные учащиеся работают устно по презентации.

Выбирается учащийся - помощник на роль СОВЫ (желательно отвлекающийся или испытывающий проблемы в изучении математики)

8 - 10 мин.

1) «СОВА» задает вопросы учащимся класса, вместе обсуждаем ответы.

1. Чем отличается изображение луча от изображения отрезка?

2. Совпадают ли лучи ВС и СВ ?

3. Совпадают ли отрезки АК и КА ?

4. Сколько общих точек могут иметь две прямые?

5. Середина отрезка - это ... ?

слайд 4

2) Назовите отрезки и прямые, которые есть на рисунке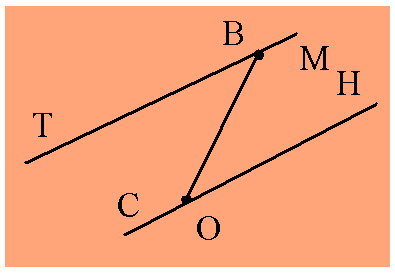

слайд 5

3) Опишите рисунок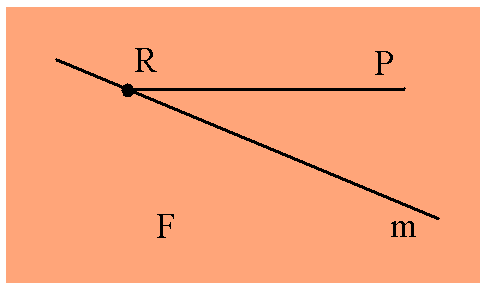

слайд 6

Работа по учебнику № 97 (а)

Одно слагаемое увеличили на 50. Как нужно изменить другое слагаемое, чтобы сумма:

• увеличилась на 80?

• увеличилась на 78?

• уменьшилась на 59?

• осталась без изменения?

слайд 7

V. Решение задач на нахождение длины отрезка.

20 -24 мин

А)

Можно разобрать фронтально ( устно).

слайд 8

Б)

Вызвать учащегося к доске.

Разобрать подробно и записать на доске.

Сравнить решение и ответ учащегося с решением и ответом на слайде.

слайд 9

5 отметка

Физкульт-минутка:

1. Нарисуйте правой рукой четыре квадрата.

2. Нарисуйте левой рукой три треугольника.

3. Нарисуйте кончиком носа букву В два раза.

2 мин

слайды 10-12

В)

Вызвать учащегося к доске.

Сравнить решение и ответ учащегося с решением и ответом на слайде.

Предложить раздаточный материал для успевающих учащихся с заданиями 4г,4д,5.

слайд 13

6 отметка

см. приложение №2

Г)

Вызвать учащегося к доске.

Сравнить решение и ответ учащегося с решением и ответом на слайде.

Рассмотреть все возможные случаи нахождения АТ.

слайд 14

7 отметка

Д)

Точка О - середина отрезка АВ = 12 см, точка D - середина отрезка АО.

Найти длину отрезка АD.

Записать решение на доске.

слайд 15

8 отметка

5) (устно) может ли:

1)длина отрезка МК быть в 3 раза больше длины отрезка МН?

2)длина отрезка МН быть в 2 раза меньше длины отрезка НК?

3)длина отрезка НК быть на 2 см меньше длины отрезка МК?

4) придумай сам вопрос по рисунку.

слайд 16

VI. Подведение итогов.

Предложить учащимся ответить на вопросы:

1. Выполнили ли мы цели урока?

2. Кто сегодня активно работал и какую отметку ему можно поставить, почему?

Если осталось время, предложить одному или нескольким учащимся проанализировать свою работу на уроке.

слайд 17

2-3 мин.

9-12 отметки

Домашнее задание.

1) С - 5.2 по вариантам;

2) §6.стр.33-34 читать;

3) №102.

Выставление отметок в дневники учащимся и журналы.

1 мин.

При подготовке урока были использованы:

• Математика. 5 класс: учебник для учащихся общеобразовательных учреждений / И.И.Зубарева, А.Г.Мордкович. - 10-е изд., стер. - М.: Мнемозина, 2010;

• Математика. 5 класс: поурочные планы по учебнику И.И.Зубаревой, А.Г.Мордковича. - 10-е изд., стер. / авт.-сост. Е. Ким. - Волгоград: Учитель, 2008;

• Коллекция Microsoft Office - cова и ослик.

Индивидуальная работа по карточкам:

КАРТОЧКА №1.

«Сравнение отрезков. Длина отрезка»

1) Выполните рисунок по описанию:

прямая ОК и луч ВС пересекаются в точке Е, а отрезок АМ пересекает прямую ОК в точке Т.2) Опишите рисунок:

3) Запишите выражение для вычисления длины отрезка ОР,

если он на 5 см короче отрезка ВС, а ВС = у см.

Раздаточный материал для успевающих учащихся с заданиями 4г,4д,5.

.

«Сравнение отрезков. Длина отрезка»

№ 4 г

АК = 32 А Т Р К

АР= 19

ТА = ?

№ 4д

Точка О - середина отрезка АВ = 12 см,

точка D - середина отрезка АО.

Найти длину отрезка АD.

№ 5

может ли :

1)длина отрезка МК быть в 3 раза больше длины отрезка МН?

2)длина отрезка МН быть в 2 раза меньше длины отрезка НК?

3)длина отрезка НК быть на 2 см меньше длины отрезка МК?

4) придумай сам вопрос по рисунку.

Дьёрдь По́йа, Джордж По́лиа - венгерский, швейцарский и американский математик.

(венг. Pólya György, англ. George Pólya или Polya; 13 декабря 1887, Будапешт, Австро-Венгрия, ныне Венгрия - 7 сентября 1985, Пало-Альто, Калифорния, США)

Окончил Будапештский университет (1912), в 1914-1940 работал в Высшей технической школе в Цюрихе (с 1928 - профессор). В 1940 переехал с женой в США, где после двух лет в университетах поступил на работу в Станфорд, в котором и прошла вся его дальнейшая научная карьера.

Основные труды по теории чисел, функциональному анализу, математической статистике (распределение Пойа) и комбинаторике (теорема Пойа</).

Живя в США, Пойа много работал со школьными учителями математики и внёс большой вклад в популяризацию науки. Он написал несколько книг о том, как люди решают задачи и как надо учить решать задачи.