Открытый урок на тему: Логарифмдік теңдеулерді шешу

Сабақтың тақырыбы: Логарифмдік теңдеулерді шешу

Сабақтың мақсаты:Білімділігі: оқушының білім, білік дағдыларын дамыту.

Дамытушылығы: Оқушылардың тез ойлау қабілеттерін арттыру, теориялық білімін практикада қолдана білу дағдысын қалыптастыру.

Тәрбиелігі: Бірлесіп жұмыс істеуге, сыйластыққа, жауапкершілікке, ұйымшылдыққа тәрбиелеу.

Сабақтың түрі: практикалық жарыс сабағы

Сабақтың көрнекілігі: тест тапсырмалары, деңгейлік тапсырмалар, бағалау парағы, слайдтар.

Сабақтың жоспары:

1. Ұйымдастыру (оқушыларды түгендеу, топқа бөлу, топ жетекшісін сайлау, бағалау парағын тарату).

2. Сабақ тапсырмаларымен таныстыру.

1-тапсырма: үй тапсырмасы бойынша қайталау сұрақтарын сұрау-

2-тапсырма: сәйкестікті тап (логарифмнің қасиеттері)

3-тапсырмаЖаңа сабақ

4-тапсырма: кім жылдам?

5-тапсырма: оқулықпен жұмыс-

6-тапсырма: тест

3. Бағалау парағы бойынша сабақты қорытындылау: топ жетекшілеріне сөз беру, оқушыларды бағалау

4. Үйге тапсырма беру

Сабақтың жүрісі:

1-тапсырма бойынша оқушыларға 10 сұрақ беріледі (әр сұрақтың жауабы-1 ұпай):

1. Қандай функцияны логарифмдік функция деп атайды?

у= (a>0, a≠1) түрінде берілген функцияны негізі а болатын логарифмдік функция деп атайды.

2. Логарифмдік функцияның анықталу облысы.

Барлық оң сандар жиыны R_+, яғни D()=(0; +∞).

3. Логарифмдік функцияның мәндерінің облысы.

Барлық нақты сандар жиыны R, яғни (-∞; +∞).

4. Логарифмдік функция қай жағдайда өспелі және кемімелі болады?

Егер a>1 болса, онда у= логарифмдік функциясы өспелі болады, егер 0</</i>

5. Қандай теңдеу логарифмдік теңдеу деп аталады?

Айнымалысы логарифм белгісінің ішінде болатын теңдеу логарифмдік теңдеу деп аталады.

2-тапсырма. Сәйкестікті тап (тақтада ілулі тұрған формулаларды сәйкестендіру):

Логарифмдердің негізгі қасиеттері

Енді логарифмдердің негізгі қасиеттерін атап өтелік. Кез келген а>0, (а≠1) және b, с оң сандары үшін

1°. log_al=0; 2°.log_ea=l;

3°. log_ab∙c=log_ab+log_ac; 4°. log, - = log_a b - log_a c;

5°. log, b^m = mlog_a b, m R; 6°. log _аⁿ b log_a b,n R,n ≠ 0;

7°. log, b = log_a c b = c; 8°. log_a

3-тапсырма.Жаңа сабақ

Қарапайым логарифмдік теңдеу log_a х = b түрінде жазылады. Бұл теңдеудің келесі түрдегі бір ғана шешімі бар: х = а^ь.

1-мысал

log₃ (х² + 4х + 4) = 2 тендеуін шешейік.

Берілген теңдеудің шешімі

х² + 4х + 4 = 3²

шартын қанағаттандыратын барлық х-тің мәндері болып табылады.

Онда келесі квадрат тендеуді шешеміз:

х²+4х-5 = 0.

1 және -5 сандары бұл теңдеудің түбірлері және алғашқы тендеудің шешімдері болыап табылады. Логарифмдік теңдеу көбінесе

log_a f(х) = log_а g(x), (a > 0, a ≠ 1) түрінде кездеседі. Мұндай теңдеулерді шешу үшін:

1. f(^x) ⁼ g(^x) теңдеуін шеігіу керек;

2. табылған түбірлер ішінен f(x) > 0 және g(x) > 0

теңсіздіктерін қанағаттандыратындарын іріктеп алу керек (логарифмдік функция тек оң сандар жиынында ғана анықталған).

Логарифмдік тендеулерді шешудің негізгі екі әдісі бар:

1) берілген тендеуді log_a f(x) = log_а g(x) түріне, содан

кейін оны f(x) = g(x) түбіне түрлендіру әдісі;

2) жада айнымалыны енгізу әдісі.

2-мысал

log₃(4x.+ 2) = log₃(x -1) тендеуін шешейік.

Берілген теңдеудің шешімін табу үшін келесі жүйені шешу қажет:

4х + 2 = х -1,

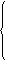4х + 2 > 0,

х-1 > 0.

х -1 саны жүйедегі теңдеу түбірі болып табылады.

болғанда, бірінші теңсіздік орындалады. Сонымен қатар болғандықтан, табылған түбір берілген теңсіздікті қанағаттандырмайдьі. Бұл түбір екінші теңсіздікті қанағаттандыратынын тексерудің қажеті жоқ.

Жауабы: берілген тендеудің түбірлері жоқ.

Логарифмдік теңдеулерді шешу кезінде логарифмнің келесі қасиеттері көбірек қолданылады:

1) көбейтіндінің логарифмі көбейткіштер логарифмдерінің қосындысына тең:

log_a(pq) = log_ap+log_aq;

2) бөлшектің логарифмі бөлшек алымының логарифмінен бөлімінің логарифмін азайтқанға тең:

3) дәреже логарифмі дәреже көрсеткішін негіздің логарифміне көбейткенге тең:

log_a р^q = q log_a p.

3-мысал

lg(x - 9) + lg(2x -1) = 2 тендеуін шешейік.

Логарифмдер қосындысы х-9 жәңе 2х-1 өрнектерінің көбейтіндісін логарифмдеу арқылы алынған:

lg(x - 9) + lg(2x -1) - lg ((х - 9)(2х -1)) Берілген теңдеуді шешу үшін логарифмдер анықтамасын пайдаланамыз:

Осы табылған түбірлер берілген тендеудің шешімдері бола ала ма, жоқ па, осыны анықтау үшін келесі теңсіздіктер жүйесін шешеміз:

х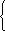-9>0,

2х-1>0.

Демек х > 9 және х > 0,5 теңсіздіктерінің қатар орындалуы қажет. Бұл жүйенің шешімі х > 9 теңсіздігі болып табылады. Осы шартты тек қана х = 13 түбірі қанағаттандырацы.

Жауабы: х- 13.

Логарифмдік теңдеулерді шешу кезінде көбінесе бір негізден екінші бір негізге ауысуға тура келеді:

4-мысал

log _x 2 - log₄ x +1 = 0 теңдеуін шешейік.

Теңдеуді шешпес бұрын бірдей бір негізге ауысу қажет. Біздің теңдеуімізде бұрыннан қатысып тұрған 4 санын жаңа негіз етіп алсақ, бұл теңдеудің шешілуін жеңілдете түседі.

Онда келесі түрдегі теңдеуді аламыз:

Тендеуге қатысып тұрған бөлшектерден құтылу үшін теңдеудің екі жағын 6 санына көбейтеміз:

Осы теңдеулерді шешсек

Жауабы:

4-тапсырма. Кім жылдамесеп беріледі, әр топтан дұрыс шығарған оқушыларға1 ұпайдан қосылып отырады

1Теңсіздікті шешіңіз: Жауабы:

2. Теңсіздікті шешіңіз: Жауабы:

3. Теңсіздікті шешіңіз: Жауабы:

4. Теңсіздікті шешіңіз: Жауабы:

5. Теңсіздікті шешіңіз: Жауабы:

6. Теңсіздікті шешіңіз: Жауабы:

7. Теңсіздікті шешіңіз: log_х(х²-2х+2) = 1 Жауабы: х =2.

8. Теңсіздікті шешіңіз: 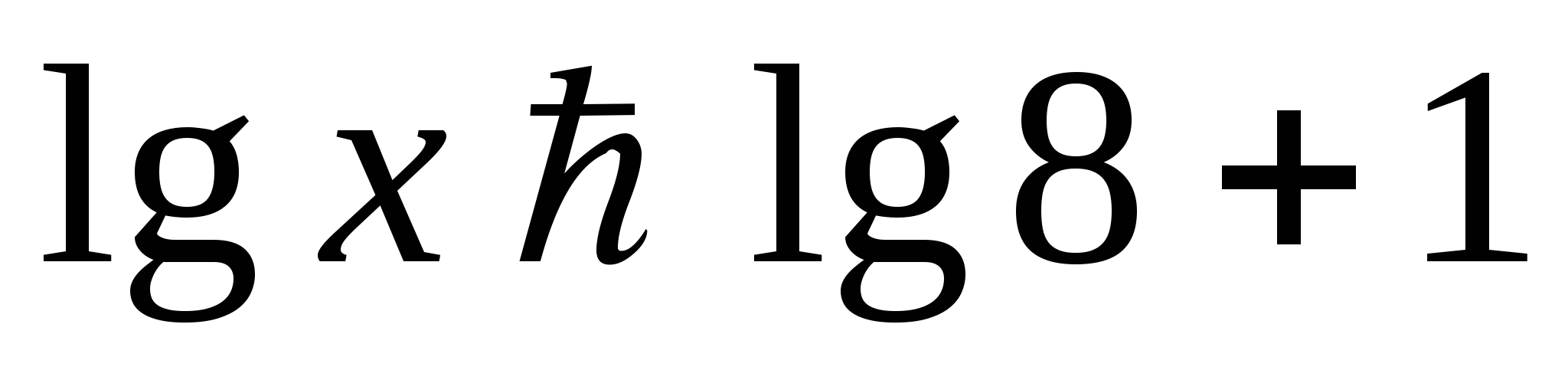Жауабы: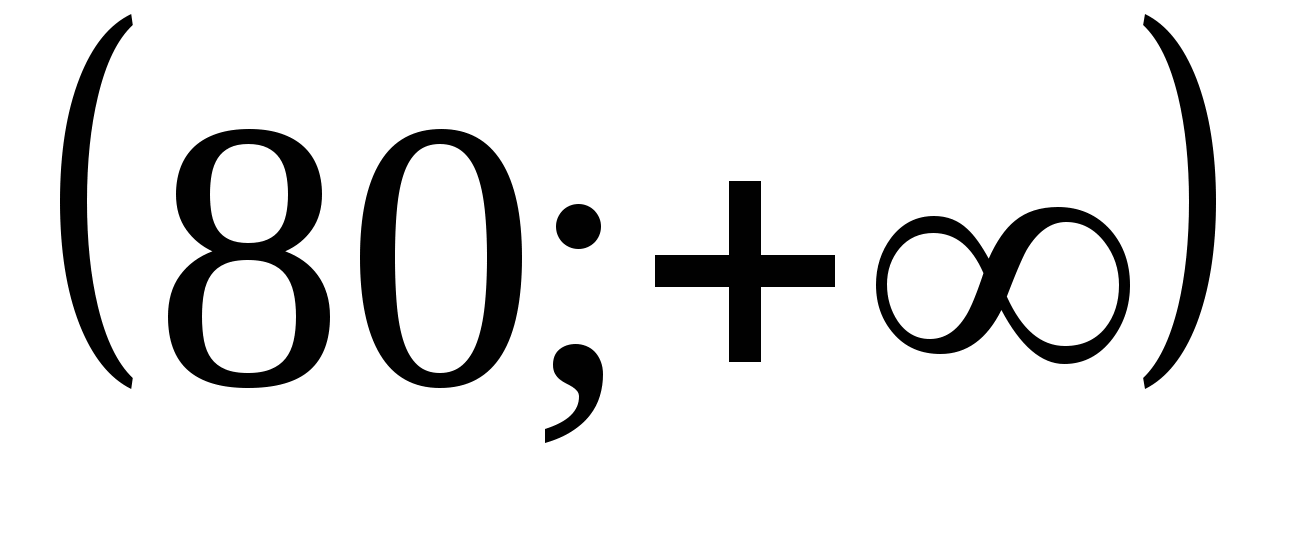

5-тапсырма. Оқулықпен жұмыс:

1-топ:№678 (а,ә).

2-топ: №680 (а,ә).

3-топ: №681(а,ә).

6-тапсырма. Тест есептері бойынша білім деңгейін тексеру:

1.Амалларни бажаринг.

1. 111,286154

2. 71,724

3. 217,62

2.Хисобланг.

1. 14,7

2. 22,05

3. 45,55

3.Хисобланг.

1. 91,57

2. 14,12

3. 90,927

4.Айиришни бажаринг.

5.Тенгламани ечинг.7

1. 

2. 

3. 2

3. Бағалау парағы бойынша

сабақты қорытындылау: топ жетекшілеріне сөз беру, оқушыларды бағалау.

4. Үйге тапсырма беру: № 677-6778

Бағалау парағы 1-топ

Оқушының аты-жөні

Сабақ барысы

+

Ұйымдастыру кезеңі

Өткен сабақты пысықтау

Сәйкесін тап

Жаңа сабақ

Кім жылдам

Оқулықпен жұмыс

тест