Разработка урока по математике на тему ' Бесконечно убывающая геометрическая прогрессия' (9 класс)

"Бесконечно убывающая геометрическая прогрессия"

Цели урока:

1. ознакомление учащихся с новым видом последовательности - бесконечно убывающей геометрической прогрессией;

2. формулирование начального представления о пределе числовой последовательности;

3. знакомство с ещё одним способом обращения бесконечных периодических дробей в обыкновенные с помощью формулы суммы бесконечно убывающей геометрической прогрессии.

Ход урока

1. Проверка домашнего задания.

1) Проверка основных формул, связанных с арифметической и геометрической прогрессиями. Два ученика готовят записи формул у доски.

2) Остальные учащиеся выполняют математический диктант по теме «Формулы суммы».

Задания:

№1. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен 6 (1-й вариант), -20 (2-й вариант), а пятый член -6 (1-й вариант), 20 (2-й вариант).

№2. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен -20(1-й вариант), 6 (2-й вариант), а разность равна 10(1-й вариант), -3(2-й вариант).

№3. Найдите сумму первых пяти членов геометрической прогрессии, если её первый член равен 1(1-й вариант), -1 (2-й вариант), а знаменатель равен -2(1-й вариант), 2(2-й вариант).

1. Изучение новой темы. (1)

Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого - половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего.

В результате, мы получили последовательность сторон квадратов 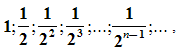образующих геометрическую прогрессию со знаменателем .

И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,

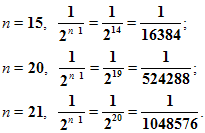
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.

Фронтальная работа.

Записать определение: геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.

С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.

Задача №1.

Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой:

а)

б) (самостоятельно)

данная последовательность не является бесконечно убывающей геометрической прогрессией.

Рассмотрим сумму n первых слагаемых.

По формуле суммы n первых членов геометрической прогрессии, она равна .

Если n неограниченно возрастает, то

Тренировочные упражнения.

Задача №2. Найти сумму бесконечно убывающей геометрической прогрессии с первым членом 3,вторым 0,3.

Задача №3. учебник [1], стр. 160, №433(1)

Найти сумму бесконечно убывающей геометрической прогрессии:

Задача №4. учебник [1], стр. 160, №434(1)

Найти сумму бесконечно убывающей геометрической прогрессии, если

Задача №4. Записать бесконечную периодическую десятичную дробь 0,(5) в виде обыкновенной дроби.

1Задача №5. учебник [1], стр. 162, №445(3) (самостоятельное решение)

Записать бесконечную периодическую десятичную дробь 0,(12) в виде обыкновенной дроби.

Подведение итогов.

1. С какой последовательностью сегодня познакомились?

2. Дайте определение бесконечно убывающей геометрической прогрессии.

3. Как доказать, что геометрическая прогрессия является бесконечно убывающей?

4. Назовите формулу суммы бесконечно убывающей геометрической прогрессии.

Домашнее задание.

№435(1;3), 445(4), 436. [1]