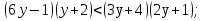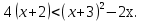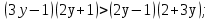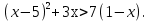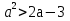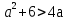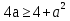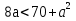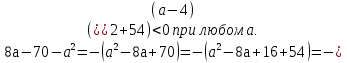Конспект урока по математике на тему 'Доказательство числовых неравенств'

Конспект урока по алгебре для 8 «А» класса

МОУ «СОШ №33» на тему:

«Доказательство числовых неравенств»

Цель урока:

• образовательная: продолжить формирование умения доказывать числовое неравенство по его определению, формирование умение решать задачи на составление и доказательство числового неравенства;

• развивающая: развитие внимания, памяти, наблюдательности;

• воспитательная: воспитание аккуратности, настойчивости, умения работать в коллективе.

Тип урока: комбинированный урок.

Методы обучения: дедуктивно-репродуктивный.

Требования к ЗУН:

Учащиеся должны знать:

• определение числового неравенства.

• правило сравнения чисел с использованием определения числового неравенства.

• правило доказательства неравенств с использованием определения числового неравенства.

Учащиеся должны уметь:

• применять определения числового неравенства для сравнения чисел.

• применять определения числового неравенства для доказательства неравенств.

Оборудование: чертежные инструменты.

Литература:

1. Алгебра: учебник для 8 классов общ-х учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и С. Б. Суворова; под ред. С. А. Теляковского - М.: Просвещение, 2010. - 287 с.

2. Алгебра: Поурочные планы по учебнику Макарычева Ю.Н., Н. Г. Миндюк, К. И. Нешкова и С. Б. Суворовой/ авт.-сост. Т.Ю. Дюмина, А. А. Махонина. - Волгоград: 8 класс. - М.: Просвещение, 2010. - 399 с.

3. Саранцев Г. И. «Методика обучения математике в средней школе: Учебное пособие для студентов мат. спец. пед. вузов и университетов» М.: Просвещение, 2002 - 224с.

План урока

1. Организационный момент (1 минута);

2. Сообщение темы и целей урока (1 минута);

3. Актуализация знаний (15 минут);

4. Формирование умений и навыков (25 минут);

5. Подведение итогов и Д/З. (3 мин.)

Ход урока

Организационный момент:

Включает в себя приветствие учителем класса, проверку готовности кабинета к проведению урока, проверку отсутствующих.

Сообщение темы и целей урока:

Учитель: Сегодня на уроке мы продолжим изучать числовые неравенства. Закрепим материал «Доказательство числовых неравенств». Это и будет тема сегодняшнего занятия.

Актуализация опорных знаний:

Учитель: Прежде чем приступить к решению заданий на закрепление темы числовых неравенств решим устно несколько примеров.

Сравните числа a и b, если дана разность a - b

Запись на доске:

а) -3; б) 0,2; в) 0;

г) (-3)⁶; д) b-a; e) .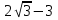

Ученик1: а) ab; в) a=b.

Ученик2: г) a>b; д) a=b; е) a>b.

Учитель: Расположите в порядке возрастания числа

Запись на доске:

1,2;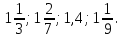

Учитель: Сравните числа

Запись на доске:

а)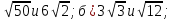

в)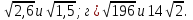

Ученик1: а) 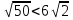; б)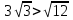

Ученик2: в)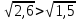; г).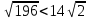

Учитель: Теперь решим самостоятельно небольшую проверочную работу.

Ученикам раздаются карточки с заданиями:

Ученики выполняют задания самостоятельно.

Решение проверочной работы:

Вариант 1

1. .

2. 

Вариант 2

Формирование умений и навыков:

Учитель: Теперь перейдем к сегодняшней теме. Открываем тетради и записываем сегодняшнее число, и тему.

Запись на доске и в тетрадях:

Дата «…»

Тема: «Доказательство числовых неравенств»

Учитель: Сегодня на уроке мы с вами закрепим понятие о числовых неравенствах и их доказательств.

Как известно, чтобы сравнить два числа нужно взять их разность и сравнить с 0. Если разность двух чисел больше нуля, то первое число больше второго, если меньше - первое число меньше, если равна нулю - числа равны. Теперь решим примеры из учебника.

Запись на доске:

№731(а, в), №733, №735 (б), №736(а), №737.

Учитель: Итак, начнем с № 731(а,в)

Учитель вызывает учащихся к доске.

(Ученики по очереди начинают выходить к доске).

а)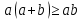

Ученик: Чтобы доказать неравенство, нужно вычислить разность левой и правой частей, тогда получим:

Запись на доске и в тетрадях:

а)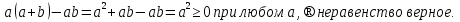

в)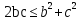

Ученик: Чтобы доказать неравенство, нужно вычислить разность левой и правой частей, тогда получим:

Запись на доске и в тетрадях:

в)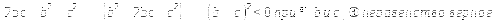

Учитель: Следующий №733

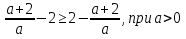
Ученик: Чтобы сравнить эти два числа, нужно вычислить их разность, тогда получим:

Запись на доске и в тетрадях:

Учитель: Следующий решаем №735 (б)

б)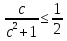

Ученик: Чтобы доказать неравенство, нужно вычислить разность левой и правой частей, тогда получим:

Запись на доске и в тетрадях:

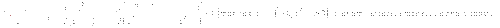
Учитель: Следующий №736(а)

а)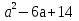

Ученик: нам нужно оценить выражение. Если внимательно посмотреть на выражение, можно заметить, что оно похоже на формулу квадрата разности. Сделаем так, чтобы выражение содержало в себе эту формулу. Получим:

Запись на доске и в тетрадях:

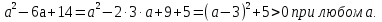
Учитель: Следующий №737. Этот номер будут решать четыре ученика одновременно. Затем мы определим общий ответ

Ученики одновременно решают у доски

Запись на доске и в тетрадях:

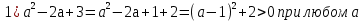
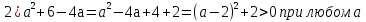
Учитель: Итак, мы решили каждое из четырех неравенств. Какое же из является неверным?

Ученики(хором): неравенство № 3

Подведение итогов:

Учитель: А сейчас давайте подведем итоги нашего урока:

- Дайте определение числового неравенства

Ученик: Числовым неравенством называется соотношение между числами, указывающее на то, какое из двух чисел больше другого

Учитель:

- Сформулируйте основное правило сравнения двух чисел

Ученик: Для того чтобы сравнить два числа, нужно рассмотреть их разность: если она больше нуля, то первое число больше другого; если меньше нуля - второе число больше первого; если равна нулю - числа равны.

Учитель: За активную работу на уроке, я ставлю следующие отметки …

На этом урок окончен, можете быть свободны.

…

Домашнее задание

Учитель: Откройте дневники и запишите задание на дом.

Запись на доске и в дневниках:

№ 735 (а), № 736 (б), № 740.

№ 735. Верно ли неравенство

а) ,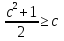

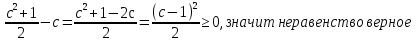
№ 736. Оценить выражение:

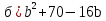
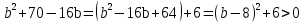
№ 740. Что больше: a³ + b³ или ab(a+b), если a и b - неравные положительные числа?

a³+b³ - ab(a+b)= a³+b³-a²b-ab²= (a³- a²b)-( ab² -b³)=a²(a-b)-b²(a-b)=(a-b)( a²-

-b²)=(a-b)(a-b)(a+b)=(a-b)²(a+b)>0 (т.к. (a-b)²>0, a и b - положительные неравные числа)⇒ a³+b³> ab(a+b).