- Учителю
- Урок по математике для 9 класса по повторению темы «Треугольники»
Урок по математике для 9 класса по повторению темы «Треугольники»
Повторение темы «Треугольники»
(9 класс, геометрия)
Цель урока: Повторить основные понятия и теоремы по теме «Треугольники».
Задача урока: уметь применять на практике теоремы и свойства различных видов треугольников.
Ход урока:
Вопросы и задания:
-
С какими видами треугольников вы встречаетесь при решении задач чаще всего? (равносторонний, равнобедренный, прямоугольный).
-
Какой треугольник называется равносторонним? (треугольник, все стороны которого равны).
-
Какой треугольник называется равнобедренным? Как называются его стороны? ( если две его стороны равны; равные стороны называются боковыми, а третья - основанием).
-
Сформулировать теоремы о свойствах равнобедренного треугольника ( а) В равнобедренном треугольнике углы при основании равны).
Задание: Найти величину неизвестного угла:

б) В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой).
5) Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? (Отрезок, соединяющий вершину треугольника с серединой противоположной стороны; три медианы).
Задание: Построить на доске медианы в данном треугольнике.
6) Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? (отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны).
Задание: Построить на доске биссектрисы в данном треугольнике.
7) Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону).
8) Поясните понятие «замечательные точки треугольника». Сколько их? (точки пересечения биссектрисс, медиан, высот, серединных перпендикуляров).
9) Какая прямая называется серединным перпендикуляром к отрезку? (прямая, проходящая через середину отрезка и перпендикулярная к нему)
Задание: Построить на доске серединные перпендикуляры в треугольнике.
10) Как связаны некоторые из этих точек с центром вписанной и описанной окружности? (точка пересечения биссектрисс - центр вписанной окружности, точка пересечения серединных перпендикуляров - центр описанной окружности).
11) Что такое периметр треугольника? (сумма длин трёх сторон).
12). Составьте формулы для вычисления периметров треугольников?

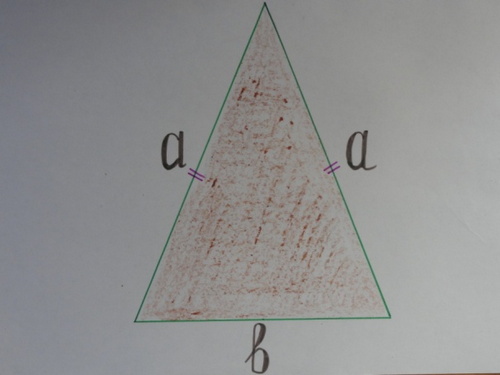
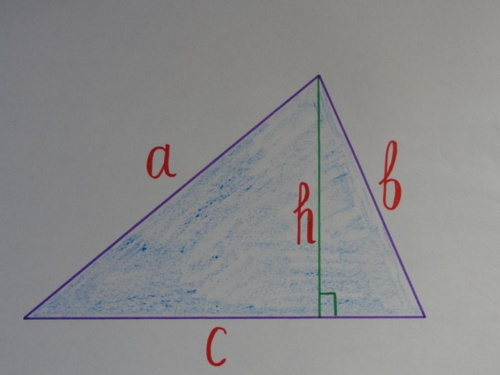
13) Какие теоремы для нахождения площади треугольников вы знаете?
( 1) Площадь треугольника равна половине произведения его основания на высоту; 2) Площадь треугольника равна половине произведения его катетов;
3) Площадь треугольника равна половине произведения двух его сторон на синус угла между ними).
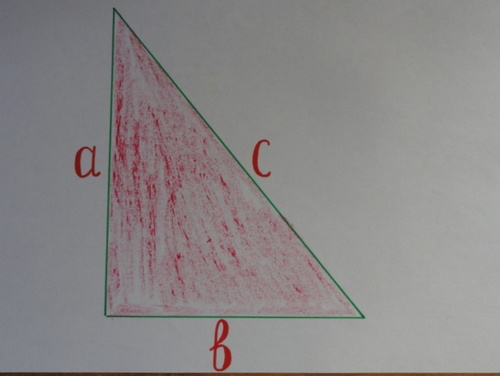
14) Вычислите площади треугольников:
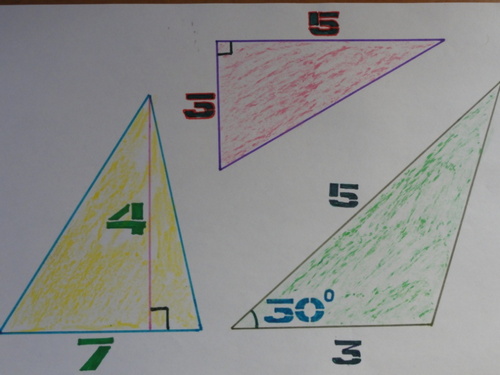
Ответ: (14; 7,5; 3, 75)
15) Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника? (Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.)
16) По данным рисунка найдите sin A, cos A, tg A.
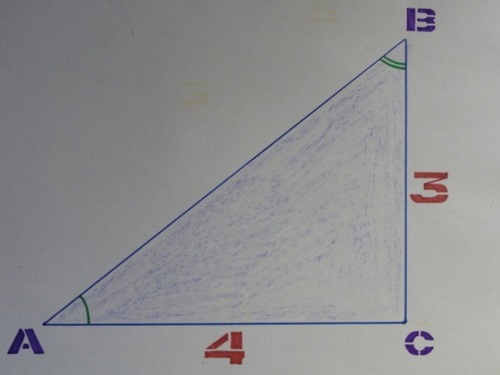
17) Как назвается прямоугольный треугольник со сторонами 3, 4, 5? (Египетский. Сообщение ученикапо «Египетскому треугольнику»; он использовался в Древнем Египте для построения прямого угла. 3,4,5 - «Пифагорова тройка»; удовлетворяют соотношению a2+b2=c2: 5, 12, 13; 6, 8, 10).
18) Что значит «Решить треугольник»? (найти все его неизвестные элементы, т.е. стороны и углы).
19) Какие теоремы мы используем при «решении треугольника»? (Теорема синусов: «Стороны треугольника пропорциональны синусам противоположных углов»; Теорема косинусов: «Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними»).
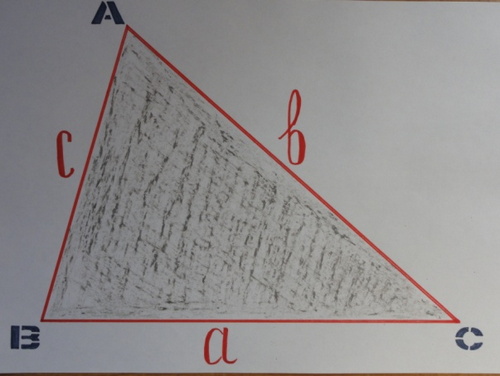
20) а) Дан треугольник МNР. Прочитайте, как используя теорему косинусов найти квадрат каждой стороны.

б) Применить теорему синусов к данному треугольнику.
21) Вычислить, используя формулы приведения и «Таблицу Брадиса» значения sin 160° ; cos 140°.
( sin 160°= sin 180°-20°)= sin20°;
cos 140°= cos 180°-40°)= - cos 40°).
22) Самостоятельная работа (дифференцированно): Задание из учебника «Геометрия 7-9, Л.С. Атанасян» № 1025 по теме «Решение треугольников» - хорошо успевающим учащимся;
задание на карточке - слабоуспевающим: (под каждым треугольником подписать необходимые геометрические термины)
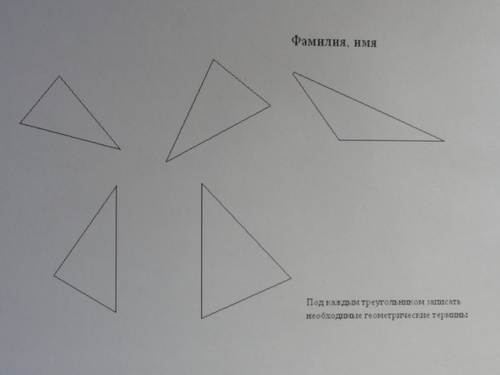
23) Взаимопроверка (ответы к заданиям даны на доске).
Подведение итога урока, выставление оценок учащимся.