- Учителю
- Урок геометрии На тему: ' Развертка пирамиды и площадь поверхности'
Урок геометрии На тему: ' Развертка пирамиды и площадь поверхности'











 Предмет:геометрия
Предмет:геометрия
Класс:11 «А»
Дата проведения:17. 10. 2014
Тема урока: Развертка пирамиды и ее площадь.
Цели и задачи урока:
Научить учащихся находить площадь пирамиды;
Совершенствовать навыки моделирования геометрических тел;
Развивать навыки работы с чертежными инструментами;
Воспитывать любовь к прекрасному;
Развивать пространственное воображение и логическое мышление.
Оборудование и ресурсы: листы А 3, листы А 4, интерактивная доска, стикеры, маркеры, презентация PowerPoint, программа aktivstudio;
Ожидаемые результаты: учащиеся умеют по данным задачи находить площадь фигуры, умеют отличать элементы пространственных тел на плоскости, умеют строить фигуры с помощью циркуля.
Тип урока: изучение новой темы;
Ход урока:
Этапы урока
Действия учителя
Действия учащихся
Орг. момент
Проверка и контроль подготовки к уроку. 1 мин
Готовятся к уроку, готовят тетради, учебники и другие принадлежности
Деление на группы
Раздает рисунки (см приложение «Рисунки»
Раздает оценочные листы.
разъясняет
1мин
Делятся на группы. Избирают роли в группе:
Координатор, контролер-оценщик,
исполнитель, спикер, таймкипер
Проверка домашнего задания
Открывает домашнее задание на интерактивной доске. 3 мин
Проверяют друг у друга
Повторение пройденных тем
Раздает задания группам.5 мин
1: домино
2: морской бой
3: соответствие и определения.
Выполняют задания в группе
Логическая минутка
Каждой группе дается одно логическое задание.
1: корова;
2: время приготовления торта;
3: зарплата компании.
5 мин
В группе обсуждают, находят решение.
Стадия вызов
Каждой группе раздает задания:
Приложение «Задание 1»
2 мин
Определяют название новой темы.
Работа с учебником
Показывает формулу площади пирамиды. 2 мин
Записывают в тетради
Стадия осмысление
Раздает листы А3
Дает задание сделать из бумаги модель пирамиды. 20 мин
На бумаге рисуют развертку пирамиды, вырезают ее, и склеивают пирамиду. Измеряют линейные измерения пирамиды и вычисляют площадь модели.
Защита моделей
3 мин
Два человека защищают модель. Отвечают на вопросы.
Показывают расчеты. Объясняют.
Д/З
1 мин
Записывают в дневники
Рефлексия. Обратная связь
2 мин
Заполняют стикеры.
Оценочный лист Название группы:
ФИ ученика
Дом зад
Повторение
Работа с моделями
Вычисление площади
Итоги урока
Кто в группе отличился больше всего(один человек):
Оценщик:
Оценочный лист Название группы:
ФИ ученика
Дом зад
Повторение
Работа с моделями
Вычисление площади
Итоги урока
Кто в группе отличился больше всего(один человек):
Оценщик:
Оценочный лист Название группы:
ФИ ученика
Дом зад
Повторение
Работа с моделями
Вычисление площади
Итоги урока
Кто в группе отличился больше всего(один человек):
Оценщик:

2. Дано:
Правильная
3-х угольная
усеченная пирамида
a= 4 дм
b=2 дм
AA1=2 лм
H -?
L=?
Pешение:
h=OO1, OA=R, O1A1=R1;R, R1-радиусы окружностей, описанных около оснований пирамиды.
 ;
;
 ;
;
Из трапеции АОО1А1
А1К ОО1
ОО1  h;
h;
AK = AO-А1О1= =
=
Из треугольника АКА1 по теореме Пифагора:
H
Из трапеции ВСС1В1
L=В1М
BM=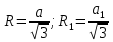
Из треугольника ВВ1М по теореме Пифагора:
L=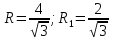
Ответ: H L=
L=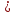
Задание 1
Ребус
Расшифровка
5555, 4, 6, 2, 5, 4, 3, 8888
Переведи
and its area
Стереометрия
Планиметрия
Раздел геометрии
Площадь прямоугольника
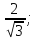
Геометрия в пространстве
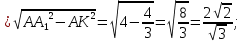
Площадь треугольника
Пифагор
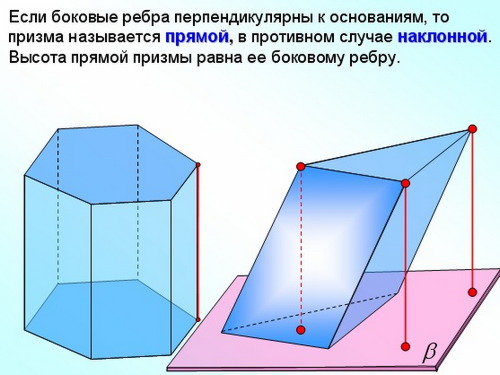
Призма
Параллелограмм
Его именем названа формула для нахождения площади треугольника с помощью полупериметра.
Автор теоремы:
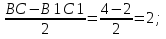

Герон
Апофема
Древне
греческий ученый
Миля
Единица измерения
Геометрия на плоскости
Фигура из трех точек, не лежащих на одной прямой
1 метр
Площадь четырех
угольника, у которого все углы прямые
Приложение «Повторение»
Морской бой
Теорема Пифагора
Площадь призмы
а=3
а=8
Sбок=40
Sбок=32
b=4
c=
c=
Sосн=40
Sполн=
Sполн=
b=6
c=
c=
Sосн=25
Sполн=
Sполн=
b=
c=7
c=12
Sосн=
Sполн=86
Sполн=124
Соответствие
№
1
-
prism
геометр. перпендикуляр, опущенный из центра правильного многоугольника на любую из его сторон, а также длина этого перпендикуляра.
2
-
apothem
многогранник, основание которого - многоугольник, а остальные грани - треугольники, имеющие общую вершину.
3
-
pyramid
самая длинная сторона прямоугольного треугольника, противоположная прямому углу.
4
area of a prism
многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани - параллелограммами, имеющими общие стороны с этими многоугольниками.
5
-
leg
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
6
-
hypotenuse
S= 2Sосн+ Sбок
7
-
sine
.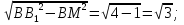
8
Pythagorean theorem
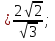
9
area of a triangle
отношение противолежащего катета к гипотенузе
10
area of a circle
сторона прямоугольного треугольника, образующая прямой угол.
Приложение «Рисунки»















Критерии оценивания
-
Проверка домашнего задания
1 задание
-
все элементы указаны правильно 2 балла
-
правильный чертеж 2 балла
-
Все определения правильны 2 балла
-
Оформление задачи
2 задание
-
Оформление задачи 2 балла
-
Правильные чертежи 2 балла
-
Решение задачи 2 балла
10-12 баллов «5»
8-10 баллов «4»
4-8 баллов «3»
-
Практическое задание
-
Красота модели 2 балла
-
Правильность модели 2 балла
-
Вычисление площади 3 балла
-
Креативность выполнения задания 2 балла
9 баллов «5»
6 баллов «4»
4 баллов «3»
Критерии оценивания
-
Проверка домашнего задания
1 задание
-
все элементы указаны правильно 2 балла
-
правильный чертеж 2 балла
-
Все определения правильны 2 балла
-
Оформление задачи
2 задание
-
Оформление задачи 2 балла
-
Правильные чертежи 2 балла
-
Решение задачи 2 балла
10-12 баллов «5»
8-10 баллов «4»
4-8 баллов «3»
-
Практическое задание
-
Красота модели 2 балла
-
Правильность модели 2 балла
-
Вычисление площади 3 балла
-
Креативность выполнения задания 2 балла
9 баллов «5»
6 баллов «4»
4 баллов «3»