- Учителю
- Сценарий занятия элективных курсов в 11 классе по теме «Методы решения алгебраических уравнений с модулем»
Сценарий занятия элективных курсов в 11 классе по теме «Методы решения алгебраических уравнений с модулем»
Сценарий занятия элективных курсов в 11 классе по теме
«Методы решения алгебраических уравнений с модулем»
В программе средней школы знакомство с модулем начинается с 6 класса при изучении темы «Рациональные числа». Даётся определение: модулем или абсолютным значением числа называют расстояние от начала отсчёта до точки, изображающей число.
Предлагается решить уравнения такого типа:
│x│= 10, │x│ = - 5, │x + 5│ = 8,
│x│ = 0, │x│ + 5 = 0.
В 7 классе модуль встречается при изучении тем: «Решение линейных уравнений», « Построение графиков вида y = kx».
Предлагается построить график функции y = │x│; y = 3│x│.
В 8 классе модуль встречается при изучении темы «Квадратный корень из степени», доказывается теорема: при любом значении x верно равенство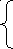 
= │x│.
Таким образом, в курсе алгебры 7 - 9 классов задачи с модулем встречаются редко, уравнения с модулями решаются самые простые, методы решения таких уравнений не рассматриваются. На ЕГЭ есть задание, содержащее модули, это С5.
Поэтому, Сегодня на занятиях мы рассмотрим тему «Методы решения алгебраических уравнений с модулем» для того, чтобы вы имели возможность лучше подготовиться к ЕГЭ.
Определение: │x│ = 
1. Решение простейших уравнений.
│ ƒ (x)│ = a
Если a > 0, то ƒ (x) = a,
ƒ (x) = - a.
Если а = 0, то ƒ (x) = 0.
Если а < 0, то корней нет.
Пример:
│2x - 3│ = 11
2x - 3 = 11, x = 7,
2x - 3 = - 11; x = - 4.
Ответ: - 4; 7.
Практикум:
1) │x│ = 3, 3) │x² + x│ = 0,
2) │x² - 4│ = 0, 4) │x² - 4x│ = 5.
2. Решение уравнений сведением к простейшему.
Пример:
│x² + x - 1│ = 2x - 1
2x - 1 ≥ 0, x ≥ 1
2
x² + x - 1 = 2x - 1, x² - x = 0,
x² + x - 1 = - 2x +1, x² +3x -2 =0.
x ≥ 1,
2
x = 0,
x = 1,
x = 
, x = 1,
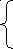x =
,
x = .
Ответ: 1; .
Практикум:
1) │x + 4│ = 2x 3) │x² + 16│ = -8x
2) │x + 4│ = -3x 4) │x² - x +3│ = x + 2
3. Решение «красивейших» уравнений.
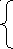ƒ (x) ≥ 0 и 
ƒ (x) ≤ 0.
Пример:
│x² - x - 2│ = x² - x - 2, │x² - 9│ = 9 - x²,
x² - x - 2 ≥ 0 x² - 9 ≤ 0.
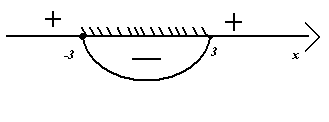
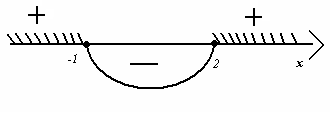
Ответ: 
Ответ: 
Практикум:
1) 7 - 4x = │4x - 7│ 3) │25x² - 1│ - 1+ 25x² = 0
2) 3x - 5 = │3x - 5│
4. Решение уравнений раскрытием модулей по определению.
Пример:
x² - 5x - │x - 6│ +9 = 0
x - 6 ≥ 0, x ≥ 6,
x² - 5x - (x - 6) + 9 = 0; x² - 6x +15 = 0; x = 3,
x - 6 < 0, x < 6, x = 1.
x² - 5x + (x - 6) + 9; x² - 4x + 3 =0
Ответ: 1; 3.
Практикум:
1) x² - │3x - 5│ = 5, 3) x² - 6x + │x - 4│ + 8 = 0,
2) x² - x - │x + 5│ - 3 = 0, 4) │x + 3│ = x² + x - 6.
5. Решение уравнений вида │ƒ (x)│ = │φ (x)│
ƒ (x) = φ (x)
ƒ (x) = - φ (x)
Пример:
│x + 3│ = │2x - 1│ x + 3 = 2x - 1 x = 4
x + 3 = - 2x + 1 x =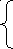 
Ответ: 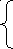; 4
Практикум:
1) │x│ = 5 - 2x 3) │x - 2│ = │2x² - 4x│
2) │x + 5│ = │10 + 4x│ 4) │x - 3│ = │3 x + 3│
6. Решение уравнений вида │ƒ (x)│ = - │φ (x)│ ƒ (x) = 0
φ (x) = 0
Пример:
│x² - 4│ = - │x ² - x - 2│ x² - 4 = 0, x = 2, x = 2
x²+ x - 2 = 0; x = - 2,
x = 2,
x = - 1;
Ответ: 2.
Практикум:
1) │x² - 9│ + │x² - 4x + 3│ = 0
2) │x² - 1│ + │x² + 6x - 7│ = 0
3) │x² + 2x - 3│ + │x² + 7x +12│ = 0
4) │x + x -2│ + │x² + 4x - 5│ = 0
7. Решение уравнений методом интервалов.
Пример:
│x + 2│ + │x - 3│ = 5
-
Найдём значение переменных x, при которых каждый из модулей равен нулю:
x = - 2, x = 3.
-
Отметим эти точки на числовой прямой. Выделим интервалы.
Определим, с каким знаком раскрывается каждый из модулей на каждом из интервалов.
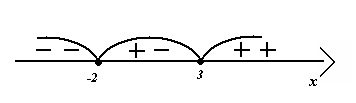
Получаем для решения этого уравнения совокупность трёх систем (так как получилось три интервала):
x < - 2, x < - 2,
- x -2 - x + 3 = 5; x = - 2;
- 2 ≤ x < 3, - 2 ≤ x < 3, x € [- 2; 3]
x + 2 - x + 3 = 5; 5 = 5;
x ≥ 3, x ≥ 3,
x + 2 + x - 3 = 5; x = 3;
Практикум:
1) │x - 3│ + 2 │x + 1│ = 4,
2) │5 - x│ + │x - 1│ = 10,
3) │x - 2│ - │5 + x│ = 3.