- Учителю
- Итоговая контрольная работа по математике для учащихся 8 класса
Итоговая контрольная работа по математике для учащихся 8 класса
Годовая контрольная работа по математике для учащихся 8 класса,
обучающихся в общеобразовательном классе, по учебникам Ш.А.Алимов и Атанасян Л.С.
Пояснительная записка
Данная контрольная работа составлена в формате ГИА по курсу математики 8 класса. Использовать её можно в качестве итогового контроля. Работа состоит из 10 заданий базового и повышенного уровня сложности. Базовая часть состоит из восьми заданий. Вторая часть - две задачи повышенного уровня сложности. В работе представлены курсы алгебры и геометрии. Темы курсов следующие:
-
Действия с дробями
-
Числовые неравенства
-
Арифметический квадратный корень
-
Решение квадратных уравнений
-
Исследование квадратного трёхчлена
-
Решение квадратных неравенств.
-
Решение систем уравнений
-
Четырёхугольники
-
Окружность и касательная, проведённая к ней.
-
Текстовая задача.
Контрольная работа рассчитана на 60 минут. Задания первой части с 1 - 7 оцениваются по одному баллу. Задание № 8 оцениваем двумя баллами. К заданиям первой части ученик даёт только краткий ответ, а к заданиям второй части развёрнутое решение. Задания 9 и 10 оцениваем по три балла. Общая максимальная сумма баллов - 15.Оценку «3» ученик получит, если наберёт от 4 - 7 баллов, оценку «4» ученик получит, если наберёт от 8 - 12баллов, выше 12 баллов оценка - «5».
Критерии оценивания задания №9
Если ученик при решении допустил вычислительную ошибку, но довёл решение до конца, то можно поставить за это задание 1балл.
Если ученик решил задание верно, то 3 балла.
Критерии оценивания задания №10
Если ученик допустил вычислительную ошибку в решении уравнения, но довёл решение до конца, то можно поставить за это задание 1балл.
Если ученик решил задание верно, то 3 балла.
№п/п
Тема задания
Примерное время выполнения
1
Действия с дробями
5мин
2
Числовые неравенства
2мин
3
Арифметический квадратный корень
2мин
4
Решение квадратных уравнений
4мин
5
Исследование квадратного трёхчлена
5мин
6
Решение квадратных неравенств.
8мин
7
Решение систем уравнений
7мин
8
Четырёхугольники
7мие
9
Окружность и касательная, проведённая к ней.
10мин
10
Текстовая задача.
10мин
Вариант№1
Первая часть
-
Найдите значение выражения
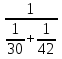
2. На координатной прямой отмечено число а.
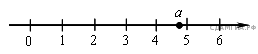
Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
1) -a 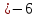
2) 5 - a 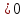
3)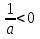
4)a - 7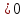
3. Какому промежутку принадлежит 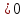
1) [3;4] 2) [4;5] 3) [5;6] 4) [6;7]
4. Найдите корни уравнения 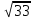
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. На рисунке изображены графики функций вида y = ax2 +вх+ c. Установите соответствие между графиками и знаками коэффициентов a и c.
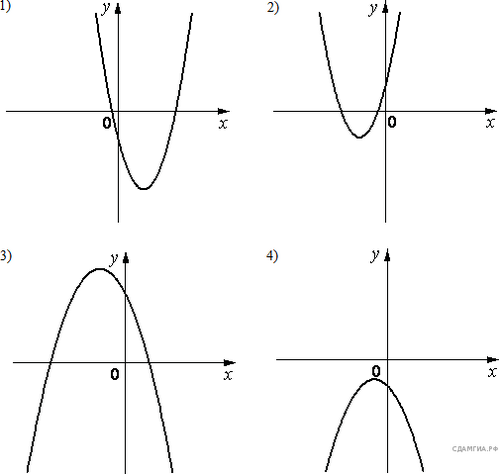
ЗНАКИ КОЭФФИЦИЕНТОВ
а) a > 0, c < 0 б) a < 0, c > 0 в) a > 0, c > 0 г) a < 0, c < 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
а
б
в
г
6. Решите неравенство 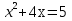
В ответе укажите номер правильного варианта.
-
(-∞; -1) (0;+∞)
-
[0;1]
-
(0;1)
-
(-∞; 0] [1;+∞)
7. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 14 см, AO = 50 cм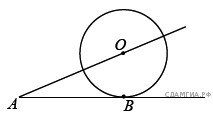 .
.
8. Основания трапеции равны 1 и 11. Найдите бóльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
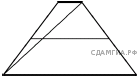
Вторая часть
9. Решите систему уравнений
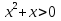
10. Из пункта А в пункт В, расстояние между которыми 19 км, вышел пешеход. Через полчаса навстречу ему из пункта В вышел турист и встретил пешехода в 9 км от В. Турист шёл со скоростью, на 1 км/ч большей, чем пешеход. Найдите скорость пешехода, шедшего из А.
Вариант2
Первая часть
1. Найдите значение выражения (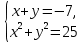
2.На координатной прямой отмечены точки x и y.
![]()
Какое из следующих неравенств верно?
-
-x
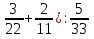
-
X + y
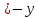
-
1 - x
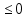
-
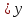
В ответе укажите номер правильного ответа
3. 3.Какому промежутку принадлежит 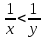
1) [8;9] 2) [7;8] 3) [6;7] 4) [9;10]
4.Найдите корни уравнения 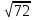
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5.На рисунке изображён график функции Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
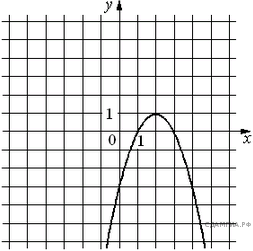
УТВЕРЖДЕНИЯ
ПРОМЕЖУТКИ
А) Функция возрастает на промежутке 1) [0; 3)
Б) Функция убывает на промежутке 2) (-∞; 2]
3) [2; 4]
4) [1; 4]
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: А Б
6. Решите неравенство 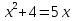 В ответе укажите номер правильного варианта.
В ответе укажите номер правильного варианта.
-
(-∞;-19) (19;+∞)
-
(-∞;-19] [(19;+∞)
-
(- 19; 19)
-
[- 19; 19]
7. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
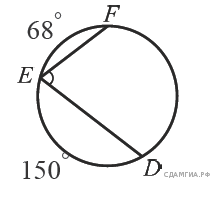
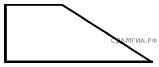
8.Тангенс острого угла прямоугольной трапеции равен 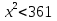 . Найдите её бóльшее основание, если меньшее основание равно высоте и равно 14.
. Найдите её бóльшее основание, если меньшее основание равно высоте и равно 14.
Вторая часть
9. Решите систему уравнений 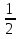
10. Расстояние от города до посёлка равно 120 км. Из города в посёлок выехал автобус. Через час после этого вслед за ним выехал автомобиль, скорость которого на 10 км/ч больше скорости автобуса. Найдите скорость автобуса (в км/ч), если известно, что в пути он сделал остановку на 24 минуты, а в посёлок автомобиль и автобус прибыли одновременно.
Вариант№3
Первая часть
1.Найдите значение выражения (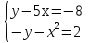
2. На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?
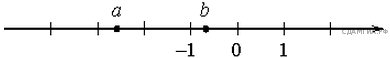
-
а + b
-
- 4
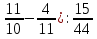
-
-
-b
В ответе укажите номер правильного варианта.
3. 3.Какому промежутку принадлежи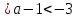
1) [6;7] 2) [7;8] 3) [8;9] 4) [9;10]
4. Найдите корни уравнения 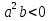
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5, Найдите значение с по графику функцииy = a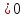 , изображенному на рисунке.
, изображенному на рисунке.
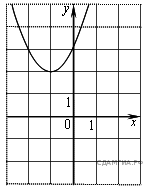
1) -2 2) 1 3) 2 4) 3
6.Решение какого из данных неравенств изображено на рисунке?
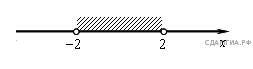
1). 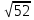 +4
+4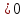
2). 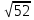 -4
-4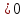
3). 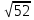 +4
+4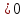
4).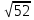 - 4
- 4
В ответе укажите номер правильного варианта.
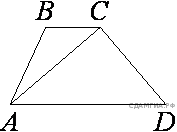
7. Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.
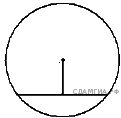
8.В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
Вторая часть
9. Решите систему уравнений
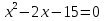
10. Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 6 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 5 км/ч?
Ответы к годовой контрольной работе для 8 класса в форме ГИА
№ вар.
1
1б
2
1б
3
1б
4
1б
5
1б
6
1б
7
1б
8
2б
9
3б
10
3б
1
17,5
1
3
-5; 1
1а;
2в;
3-б;
4-г
1
48
3
(-4;-3)и
(-3;-4
2
2,1
1
1
1;4
А-2
Б-4
1
71
28
(1;-3)и
(-6;-28)
40
3
2,16
4
2
-3;5
4
4
24
5,5
(1;3)и
(-1;3)
8,4