- Учителю
- Проект 'Виды симметрии'
Проект 'Виды симметрии'






 Научно-практическая конференция
Научно-практическая конференция
МОУ «Средняя общеобразовательная школа № 23»
города Вологды
секция: естественно - научная
проектно-исследовательская работа
ВИДЫ СИММЕТРИИ
Выполнила работу ученица 8 «а» класса
Кренёва Маргарита
Руководитель: учитель математики высшей
категории Мочалыгина Ирина Анатольевна
2014 год
Структура проекта:
1. Введение.
2. Цели и задачи проекта.
3. Виды симметрии :
3.1. Центральная симметрия;
3.2. Осевая симметрия;
3.3. Зеркальная симметрия (симметрия относительно плоскости);
3.4. Поворотная симметрия;
3.5. Переносная симметрия.
4. Выводы.
Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.
Г. Вейль
Введение.
Тема моей работы была выбрана после изучения раздела «Осевая и центральная симметрия» в курсе «Геометрия 8 класса». Меня очень заинтересовала эта тема. Я захотела узнать: какие виды симметрии существуют, чем они отличаются друг от друга, каковы принципы построения симметричных фигур в каждом из видов.
Цель работы: Знакомство с различными видами симметрии.
Задачи:
-
Изучить литературу по данному вопросу.
-
Обобщить и систематизировать изученный материал.
-
Подготовить презентацию.
В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота». В переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей чего-либо по противоположным сторонам от точки, прямой или плоскости.
Существуют две группы симметрий.
К первой группе относится симметрия положений, форм, структур. Это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией.
Вторая группа характеризует симметрию физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать физической симметрией.
Я остановлюсь на изучении геометрической симметрии.
В свою очередь, геометрической симметрии существует тоже несколько видов: центральная, осевая, зеркальная (симметрия относительно плоскости) радиальная (или поворотная), переносная и другие. Я рассмотрю сегодня 5 видов симметрии.
-
Центральная симметрия
Две точки А и А1 называются симметричными относительно точки О, если они лежат на прямой, проходящей через т О и находятся по разные стороны от неё на одинаковом расстоянии. Точка О называется центром симметрии.

Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры, говорят, что фигура обладает центральной симметрией.
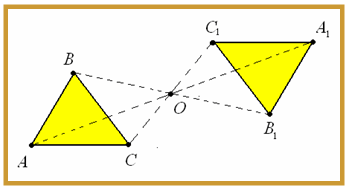
Примерами фигур, обладающими центральной симметрией является окружность и параллелограмм.


Фигуры, изображённые на слайде симметричны, относительно некоторой точки
2. Осевая симметрия
Две точки X и Y называются симметричными относительно прямой t, если эта прямая проходит чрез середину отрезка ХУ и перпендикулярна к нему. Также следует сказать, что каждая точка прямой t считается симметричной сама себе.
Прямая t - ось симметрии.
Фигура называется симметричной относительно прямой t, если для каждой точки фигуры симметричная ей точка относительно прямой t также принадлежит этой фигуре.
Прямая t называется осью симметрии фигуры, говорят, что фигура обладает осевой симметрией.
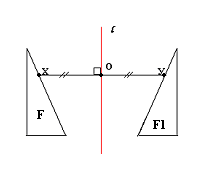
Осевой симметрией обладают неразвёрнутый угол , равнобедренный и равносторонний треугольники, прямоугольник и ромб, буквы (смотри презентацию).

-
Зеркальная симметрия (симметрия относительно плоскости)
Две точки Р1 и Р называются симметричными относительно плоскости а если они лежат на прямой, перпендикулярной плоскости а, и находятся от неё на одинаковом расстоянии
Зеркальная симметрия хорошо знакома каждому человеку. Она связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура зеркально симметрична другой.
На плоскости фигурой с бесчисленным множеством осей симметрии был круг. В пространстве бесчисленное множество плоскостей симметрии имеет шар.
Но если круг является единственным в своем роде, то в трехмерном мире имеется целый ряд тел, обладающих бесконечным множеством плоскостей симметрии: прямой цилиндр с кругом в основании, конус с круговым основанием, шар.
Легко установить, что каждая симметричная плоская фигура может быть с помощью зеркала совмещена сама с собой. Достойно удивления, что такие сложные фигуры, как пятиконечная звезда или равносторонний пятиугольник, тоже симметричны. Как это вытекает из числа осей, они отличаются именно высокой симметрией. И наоборот: не так просто понять, почему такая, казалось бы, правильная фигура, как косоугольный параллелограмм, несимметрична.
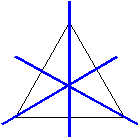
4. Поворотная симметрия (или радиальная симметрия)
Поворотная симметрия - это симметрия, сохраняющаяся форму предмета при повороте вокруг некоторой оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … Указанную ось называют поворотной осью n-го порядка.
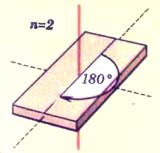
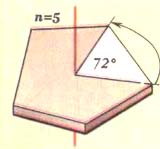
При п=2 все точки фигуры поворачиваются на угол 1800 (3600 /2 = 1800 )вокруг оси, при этом форма фигуры сохраняется, т.е. каждая точка фигуры переходит в точку той же фигуры(фигура преобразуется сама в себя). Ось называют осью второго порядка.
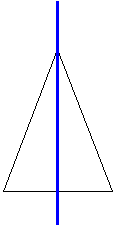
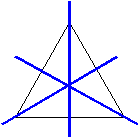
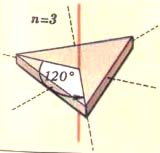
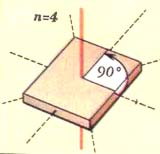
На рисунке 2 показана ось третьего порядка, на рисунке 3 - 4 порядка, на рисунке 4 - 5-го порядка.
Предмет может иметь более одной поворотной оси: рис.1 - 3оси поворота, рис.2 -4 оси, рис 3 - 5 осей, рис. 4 - только 1 ось
Всем известные буквы «И» и «Ф» обладают поворотной симметрией Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой. Иными словами, буква «И» симметрична относительно поворота на 180°, 180°= 360° : 2, n =2 , значит она обладает симметрией второго порядка.
Заметим, что поворотной симметрией второго порядка обладает также буква «Ф».
Кроме того буква и имеет центр симметрии, а буква Ф ось симметрии
Вернемся к примерам из жизни: стакан, конусообразный фунтик с мороженым, кусочек проволоки, труба.
Если мы повнимательней присмотримся к этим телам, то заметим, что все они, так или иначе состоят из круга, через бесконечное множество осей симметрии которого проходит бесчисленное множество плоскостей симметрии. Большинство таких тел (их называют телами вращения) имеют, конечно, и центр симметрии (центр круга), через который проходит по меньшей мере одна поворотная, ось симметрии.
Отчетливо видна, например, ось у конуса фунтика с мороженым. Она проходит от середины круга (торчит из мороженого!) до острого конца конуса-фунтика. Совокупность элементов симметрии какого-либо тела мы воспринимаем как своего рода меру симметрии. Шар, без сомнения, в отношении симметрии является непревзойденным воплощением совершенства, идеалом. Древние греки воспринимали его как наиболее совершенное тело, а круг, естественно, как наиболее совершенную плоскую фигуру.
Для описания симметрии конкретного объекта надо указать все поворотные оси и их порядок, а также все плоскости симметрии.
Рассмотрим, например, геометрическое тело, составленное из двух одинаковых правильных четырехугольных пирамид.
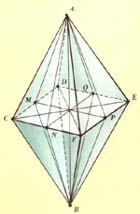
Оно имеет одну поворотную ось 4-го порядка (ось АВ), четыре поворотные оси 2-го порядка (оси СЕ, DF, MP, NQ), пять плоскостей симметрии (плоскости CDEF, AFBD, ACBE, AMBP, ANBQ).
5. Переносная симметрия
Ещё одним видом симметрии является переносная симметрия.
О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние «а» либо расстояние, кратное этой величине, она совмещается сама с собой Прямая, вдоль которой производится перенос, называется осью переноса, а расстояние «а» - элементарным переносом, периодом или шагом симметрии.
а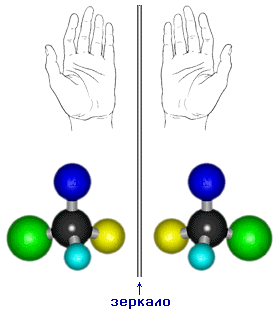
Периодически повторяющийся рисунок на длинной ленте называется бордюром. На практике бордюры встречаются в различных видах (настенная роспись, чугунное литье, гипсовые барельефы или керамика). Бордюры применяют маляры и художники при оформлении комнаты. Для выполнения этих орнаментов изготавливают трафарет. Передвигаем трафарет, переворачивая или не переворачивая его, обводим контур, повторяя рисунок, и получается орнамент (наглядная демонстрация).
Бордюр легко построить с помощью трафарета (исходного элемента), сдвигая или переворачивая его и повторяя рисунок. На рисунке изображены трафареты пяти видов: а) несимметричный; б, в) имеющие одну ось симметрии: горизонтальную или вертикальную; г) центрально-симметричный; д) имеющий две оси симметрии: вертикальную и горизонтальную.

Для построения бордюров используют следующие преобразования:
а) параллельный перенос; б) симметрию относительно вертикальной оси; в) центральную симметрию; г) симметрию относительно горизонтальной оси.
Аналогично можно построить розетки. Для этого круг делят на n равных секторов, в одном из них выполняют образец рисунка и затем последовательно повторяют последний в остальных частях круга, поворачивая рисунок каждый раз на угол 360°/n .
Наглядным примером применения осевой и переносной симметрии может служить забор, изображённый на фотографии.

Вывод: Таким образом, существуют различные виды симметрии, симметричные точки в каждом из этих видов симметрии строятся по определённым законам. В жизни мы повсюду встречаемся тем или иным видом симметрии, а часто у предметов, которые нас окружают, можно отметить сразу несколько видов симметрии. Это создаёт порядок, красоту и совершенство в окружающем нас мире.
ЛИТЕРАТУРА:
-
Справочник по элементарной математике. М.Я. Выгодский. - Издательство « Наука». - Москва 1971г. - 416стр.
-
Современный словарь иностранных слов. - М.: Русский язык, 1993г.
-
История математики в школе IX - X классы. Г.И. Глейзер. - Издательство «Просвещение». - Москва 1983г. - 351стр.
-
Наглядная геометрия 5 - 6 классы. И.Ф. Шарыгин, Л.Н. Ерганжиева. - Издательство «Дрофа», Москва 2005г. - 189стр.
-
Энциклопедия для детей. Биология. С. Исмаилова. - Издательство «Аванта+». - Москва 1997г. - 704стр.
-
Урманцев Ю.А. Симметрия природы и природа симметрии - М.: Мысль
-
Гильде В. Зеркальный мир. - М.: Мир, 1982г.
-
Ресурсы сети Интернет. , sapr.mgsu.ru/biblio/arxitekt/arhkomp2.htm, , ru.wikipedia.org/wiki/