Рабочая программа платных образовательных услуг по математике Математика для увлечённых

Зеленогайский филиал

муниципального бюджетного общеобразовательного учреждения Заворонежской средней общеобразовательной школы

«Утверждена»

на заседании

методического совета школы

Протокол №_______________

от___________________ года

РАБОЧАЯ ПРОГРАММА

ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ

(платные образовательные услуги)

«Математика для увлечённых»

(общеинтеллектульное направление)

возраст обучающихся 10 - 11 лет

срок реализации 1 год

Составитель:

учитель математики

Конюхова Елена Евгеньевна

2016-2017 учебный год

Пояснительная записка

Сделать серьёзные занятия

занимательными - вот задача

первоначального обучения.

К.Д.Ушинский.

Программа «Математика для увлечённых» реализуется по общеинтеллектуальному направлению внеурочной деятельности. Программа направлена на то, чтобы вызвать у обучающихся интерес к математике, на формирование и развитие способностей и личности ребёнка.

К числу наиболее актуальных проблем относятся высокие темпы обновления научных знаний, технологий и технических систем, применяемых не только на производстве, но и в быту, сфере досуга человека. Поэтому впервые в истории образования необходимо учить личность, постоянно самостоятельно обновлять те знания и навыки, которые обеспечивают ее успешную учебную и внеучебную деятельность, формировать готовность к освоению требований основного и полного среднего образования, совершать в будущем обоснованный выбор своего жизненного пути и соответствующей способностям, общественным потребностям профессии. Школа становится учреждением, формирующим навыки самообразования и самовоспитания.

Необходимость введения курса «Математика для увлечённых» обусловлена с внедрением Федеральных государственных образовательных стандартов нового поколения, призванных обеспечивать развитие системы образования в условиях изменяющихся запросов личности и семьи, ожиданий общества и требований государства в сфере образования. Следствием быстрого обновления знаний становится требование непрерывного образования на основе умения учиться. В современном обществе смысл и значение образования меняются. Теперь это не просто усвоение знаний, а импульс к развитию способностей и ценностных установок личности обучающегося. Сегодня происходит изменение парадигмы образования - от парадигмы знаний, умений и навыков к парадигме развития личности обучающегося. Главной целью образования становится не передача знаний и социального опыта, а развитие личности обучающегося.

Изучение данного курса тесно связано с такими дисциплинами, как математика и информатика.

Новизна программы состоит в том, что данная программа дополняет и расширяет математические знания, прививает интерес к предмету и позволяет использовать эти знания на практике. Программа делает системную разработку приёмов и форм работы развивающего характера в процессе обучения школьников, что даёт возможность сделать доступным для обучающихся освоение учебного материала при меньшей затрате времени и с большей эффективностью.

Актуальность программы определяется рядом факторов практического характера: ориентирование на исследовательскую, творческую самореализацию обучающегося, на общение учителя и обучающегося, и немаловажное - занятость ученика во внеурочное время.

В настоящее время математике отводится ответственная роль в развитии и становлении активной, самостоятельной мыслящей личности, готовой конструктивно и творчески решать возникающие перед обществом задачи. Именно математика вносит большой вклад в развитие логического мышления детей, воспитание таких важных качеств научного мышления, как

критичность и обобщённость, формирование способности к анализу и синтезу, умений выдвинуть и сформулировать логически обоснованную гипотезу. Математикой воспитываются и такие качества ума и речи, как точность, чёткость и ясность. Развитие мышления повышает интерес к знаниям, воспитывает пытливость мысли и увлечённость детей.

Педагогическая целесообразность программы объясняется формированием приёмов умственной деятельности: анализа, синтеза, сравнения, классификации, аналогии и обобщения.

Программа «Математика для увлечённых» способствует у младших школьников формированию:

• способности использования начальных математических знаний для описания и объяснения окружающих предметов, процессов, явления, а также оценки их количественных и пространственных отношений;

• пространственного воображения и математической речи, измерения, пересчёта, прикидки и оценки;

• умение активно использовать речевые средства для решения коммуникативных и познавательных задач.

Данная программа позволяет обучающимся познакомиться со многими интересными вопросами математики на данном этапе обучения, выходящими за рамки школьной программы. В программе выделены три блока: «Математика вокруг нас», «В мире задач», «Путешествие в страну Геометрия».

Решение нестандартных задач позволяет обучающимся накапливать опыт сопоставления и наблюдения, выявлять несложные закономерности, высказывать гипотезы. Основным принципом построения курса является: связь с жизнью; наиболее распространённые формы работы с детьми - работа в парах, в группах, индивидуальная.

С помощью специально подобранных задач хочется показать обучающимся красоту и простоту логического рассуждения, приводящего к решению задачи. Что способствует эстетическому воспитанию обучающихся и повышению их математической культуры. Важно, развивая интерес школьников к предмету, учить их самостоятельно работать, развивать свои способности.

В основе заданий, которые предлагается выполнить детям, лежит игра, преподносимая на фоне познавательного материала. Данная программа построена так, что большую часть материала обучающиеся не просто активно запоминают, а фактически сами открывают, разгадывают, расшифровывают, составляют. При этом идёт развитие основных интеллектуальных качеств: умения анализировать, синтезировать, обобщать, конкретизировать, абстрагировать, переносить, а также развиваются все виды памяти, внимания, воображение, речь, расширяется словарный запас.

Цель программы «Математика для увлечённых» - развитие самостоятельного поискового, исследовательского мышления, формирование творческой активности обучающихся.

Главным условием реализации этой цели в учебных заданиях выступает их направленность на то, чтобы обучающиеся применяли полученные знания в новых, нестандартных условиях.

Основные задачи программы:

1. Воспитывать интерес к предмету через занимательные упражнения.

2. Обучить методике выполнения логических заданий.

3. Формировать усидчивость, терпение.

4. Научить анализировать представленный объект невысокой степени сложности, мысленно расчленяя его на основные составные части.

5. Создать прочную основу для дальнейшего обучения этому предмету.

Формы организации учебного процесса

Организация обучения и благожелательных отношений как между педагогом и обучающимся, так и между самими обучающимися в ходе реализации методов обучения определяет характер духовных отношений в ученическом коллективе, формируют его психологический климат.

Программой предусмотрены различные типы занятий:

• Уроки-исследования

• Уроки - викторины

• Ролевые игры

• Уроки праздники

• Практическая работа

• Олимпиады

Организация деятельности школьников на занятиях основывается на следующих принципах:

• занимательность;

• научность;

• сознательность и активность;

• наглядность;

• доступность;

• связь теории с практикой;

• индивидуальный подход к учащимся.

Режим занятий:

Программа рассчитана на 1 год обучения , 66 учебных часов.

Периодичность занятий - 2 раза в неделю по 1 часу.

Ожидаемые результаты обучения по программе:

В результате обучения у обучающихся должны быть сформированы:

• умения организовывать свою деятельность - определять ее цели и задачи, выбирать средства реализации целей и применять их на практике, взаимодействовать с другими людьми в достижении общих целей, оценивать достигнутые результаты;

• умения на основе приобретенных знаний объяснять явления действительности - природной, социальной, культурной, технической среды, т. е. выделять их существенные признаки, систематизировать и обобщать, устанавливать причинно-следственные связи, оценивать их значимость, выдвигать и проверять гипотезы;

• умения ориентироваться в мире социальных, нравственных и эстетических ценностей - различать факты, суждения и оценки, их связь с определенной системой ценностей, формулировать и обосновывать собственную позицию;

• умения решать проблемы, связанные с выполнением человеком определенной социальной роли (избирателя, потребителя, пользователя, жителя определенной местности и т. д.), - обладать способностью анализировать конкретные жизненные ситуации и выбирать и реализовывать способы поведения, адекватные этим ситуациям;

• ключевые (универсальные) навыки - решения проблем, принятия решений, работы с информацией, ее поиска, анализа и обработки, коммуникации, сотрудничества;

• способность ориентироваться в мире профессий, в ситуации на рынке труда и в системе профессионального образования, в собственных интересах и возможностях, экономических условиях;

Обучающиеся должны уметь:

• самостоятельно пополнять знания по математике;

• пользоваться справочной и дополнительной литературой;

• выполнять операции сравнения и обобщения, синтеза и анализа;

• строить умозаключения, уметь рассуждать, догадываться, доказывать предлагаемое суждение.

• предполагается участие детей в конкурсах различного уровня;

• воспринимать и осмысливать полученную информацию, владеть способами обработки данной информации;

• определять учебную задачу;

• ясно и последовательно излагать свои мысли, аргументировано доказывать свою точку зрения;

• сознательно управлять своей памятью и регулировать ее проявления, владеть рациональными приемами запоминания;

• владеть навыками поисковой и исследовательской деятельности;

• использовать основные приемы мыслительной деятельности;

• самостоятельно мыслить и творчески работать;

• владеть нормами нравственных и межличностных отношений.

Программа по математике направлена на формирования следующих умений:

Интеллектуальные умения:

• умение вести доказательные рассуждения;

• умения выдвигать гипотезы;

• умение осуществлять на конкретных примерах переход от общих утверждений к частным и наоборот;

• умение составления алгоритма, работа с ними и др.

Практические умения:

• умения пользоваться математическим языком, делать записи;

• умение выполнять вычислительные операции с выражениями различной природы;

• умение проводить исследования, применяя методы математического анализа.

Формирование универсальных учебных действий (УУД)

Личностные - личностное самоопределение; действие смыслообразования, действие нравственно-этического оценивания.

Регулятивные - способность принимать, сохранять цели и следовать им в учебной деятельности;

умение действовать по плану и планировать свою деятельность

умение контролировать процесс и результаты своей деятельности, включая осуществление предвосхищающего контроля в сотрудничестве с учителем и сверстниками;

умение адекватно воспринимать оценки и отметки;

умение различать объективную трудность задачи и субъективную сложность;

умение взаимодействовать со взрослым и со сверстниками в учебной деятельности.

Познавательные - самостоятельное выделение и формулирование познавательной цели;

поиск и выделение необходимой информации;

применение методов информационного поиска, в том числе с помощью компьютерных средств;

знаково-символические - моделирование; умение структурировать знания; умение осознанно и произвольно строить речевое высказывание в устной и письменной форме;

выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;

рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности;

определение основной и второстепенной информации;

синтез, выбор оснований и критериев для сравнения, классификации объектов;

установление причинно-следственных связей; построение логической цепи рассуждений; доказательство.

Коммуникативные - умение договариваться, находить общее решение практической задачи (приходить к компромиссному решению) даже в неоднозначных и спорных обстоятельствах (конфликт интересов);

умение не просто высказывать, но и аргументировать свое предложение, умение и убеждать, и уступать;

способность сохранять доброжелательное отношение друг к другу в ситуации спора и противоречия интересов, умение с помощью вопросов выяснять недостающую информацию;

способность брать на себя инициативу в организации совместного действия, а также осуществлять взаимный контроль и взаимную помощь по ходу выполнения задания.

Обучающиеся освоят следующие УУД:

Личностные - профессиональное, жизненное самоопределение.

Регулятивные - целеустремленности и настойчивости в достижении целей, готовности к преодолению трудностей и жизненного оптимизма:

преодоление импульсивности, непроизвольности;

волевая саморегуляция.

Познавательные - постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера;

анализ объектов с целью выделения признаков;

выдвижение гипотез и их обоснование;

формулирование проблемы;

самостоятельное создание способов решения проблем творческого и поискового характера.

Коммуникативные - распределение начальных действий и операций, заданное предметным условием совместной работы;

обмен способами действия, заданный необходимостью включения различных для участников моделей действия в качестве средства для получения продукта совместной работы;

взаимопонимание, определяющее для участников характер включения различных моделей действия в общий способ деятельности;

коммуникация (общение), обеспечивающая реализацию процессов распределения, обмена и взаимопонимания;

планирование общих способов работы, основанное на предвидении и определении участниками адекватных задаче условий протекания деятельности и построения соответствующих схем (планов работы);

рефлексия, обеспечивающая преодоление ограничений собственного действия относительно общей схемы деятельности.

Учебно-тематический план

66 часовк/ч

теории

к/ч

практики

Всего часов

1. Математика вокруг нас (21 ч)

1

Из истории мер длины.

1

1

2

Из истории мер массы. Разнообразие весов.

1

1

3

Арифметика со счётами.

1

1

4

Игры с таблицей умножения.

1

1

5

Решаем уравнения с увлечением.

1

1

6

Расставь знаки арифметических действий.

1

1

7

Происхождение математических знаков.

1

1

8

Числовые ребусы. Магические квадраты.

1

1

9

Составляем кроссворды.

1

1

10

Умножение и деление круглых чисел.

1

1

11

Арифметические ребусы и лабиринты.

1

1

12

Запись цифр и действий у других народов.

1

1

13

Действия с римскими цифрами.

1

1

14

Интересные приёмы устных и полуписьменных вычислений..

1

1

15

Закономерности в числах и фигурах. Многозначные числа.

1

1

16

Игры на развитие наблюдательности. Прикидка суммы и разности при работе с многозначными числами.

1

1

17

Числа великаны и числа малютки.

1

1

18

Множества.

1

1

19

Виды алгоритмов. Линейные алгоритмы. Алгоритмы с ветвлением. Алгоритмы с повторениями.

1

1

20

Поиск альтернативных способов действий. Арифметические действия с круглыми числами.

1

1

21

Олимпиада по разделу «Математика вокруг нас»

1

1

2. В мире задач (23ч)

22

Графическое моделирование.

1

1

23

Задачи на переливание.

1

1

24

Задачи с лишними или недостающими данными.

1

1

25

Решение задач с помощью таблицы.

1

1

2

26

Старинные задачи на дроби.

1

1

2

27

Комбинаторные задачи.

Комбинации и расположения.

1

1

28

Задачи на взвешивание.

1

1

29

Задачи на планирование действий.

1

1

2

30

Игры с числами. Решение задач на нахождение части числа , числа по его части.

1

1

31

Отважный путешественник. Решение задач на нахождение скорости, времени и расстояния.

1

1

2

32

Старинные задачи на движение.

1

1

2

33

Решение задач на развитие смекалки и сообразительности.

1

1

34

Задачи на составление уравнения.

1

1

2

35

Задачи с многовариантными решениями.

1

1

2

36

Решение нестандартных задач.

1

1

37

Олимпиада по разделу «В мире задач»

1

1

3. Путешествие в страну Геометрия (22ч)

38

Урок- путешествие «Страна Геометрия»

1

1

39

Линейные орнаменты (бордюры).

1

1

40

Оригами.

1

2

3

41

Геометрические фигуры. Площадь и периметр.

1

1

2

42

Задачи на разрезание и складывание фигур, приближенное вычисление их площадей.

1

1

2

43

Площадь. Вычисление площади фигур сложной конфигурации.

1

1

2

44

Волшебный квадрат. Нахождение объёма фигур.

1

1

2

45

Конструирование узоров из геометрических фигур.

1

1

46

Игры на развитие конструкторских способностей.

1

1

47

Построение симметрических фигур - узоров. Осевая симметрия. Поворотная симметрия.

1

1

48

Зеркальное отражение. Симметрия Симметричное вырезание.

2

2

49

Путешествие по числовому лучу. Координаты на числовом луче.

1

1

2

50

Числовой луч. Координаты на луче. Сетки. Игра «Морской бой».

1

1

51

Олимпиада по разделу «Путешествие в страну Геометрия»

1

1

Всего:

17

49

66

Содержание изучаемой программы

1. Математика вокруг нас (21 ч)

Историческая справка из истории мер длины и массы. Раскрытие смысла арифметической операции на конкретной основе в процессе выполнения операций над группами предметов. Введение соответствующей символики и терминология. Табличные случаи умножения.

Составление математических кроссвордов. Составление арифметических ребусов, лабиринтов. Решение уравнений с загадкой.

Запись цифр и действий разных народов. Римская нумерация. Установление закономерностей в числах и фигурах. Игры на развитие наблюдательности. Игры с числами великанами и числами малютками. Составление множеств. Работа с алгоритмами.

Практические работы (17ч); теория (4ч); олимпиада по разделу «Математика вокруг нас».

2. В мире задач (23ч)

Решение задач, требующих от учащихся внимательной работы с текстом, с оформлением в виде таблицы. Решение задач, в которых требуется проверить, какие из высказанных предположений соответствуют действительности.

Составление занимательных и нестандартные задач. Решение логических задач с помощью таблиц. Решение старинных задач на дроби. Решение задач с помощью уравнений. Затруднительные положения: задачи на переливания, взвешивания. Составление задач на одновременное движение, встречное движение и движение в противоположном направлении.

Планирование действий при решении различных видов задач. Решение различных видов задач на движение. Моделирование задач. Задача и уравнение. Решение олимпиадных задач международного конкурса «Кенгуру».

Практические работы (16ч); теория (7ч); олимпиада по разделу «В мире задач».

3. Путешествие в страну Геометрия (22ч).

Старинные меры измерений. Составление таблиц известных мерок и придумывание новых мерок, исследовательские творческие задания. Преобразование геометрических фигур на плоскости по заданной программе и составление своих подобных заданий. Конструирование геометрических фигур.

Оценка периметра и площади. Приближённое вычисление площадей. Конструирование фигур. Вычисление площади составных фигур. Конструирование узоров. Построение симметрических фигур-узоров.

Решение задач на разрезание и складывание фигур. Нахождение объёма фигур. Путешествие по числовому лучу, определение координат. Знакомство с игрой «Морской бой». Стратегии.

Практические работы (16ч); теория (6ч); олимпиада по разделу «Путешествие в страну Геометрия»

Формы организации образовательного процесса:

• ролевые игры;

• уроки праздники;

• соревнования;

• практическая работа;

• олимпиада.

Методическое обеспечение программы

• Методические разработки занятий.

• Подробный и обогащённый материал по темам курса.

• Методическая литература по математике.

• Сборник игр и упражнений для проведения тренингов.

• Методика организации групповых, практических занятий с учётом индивидуальных особенностей.

Дидактический материал

• Модели объёмных геометрических фигур.

• Модели плоских геометрических фигур.

• Математические таблицы.

• Компьютерные программы.

• Дидактический материал по темам программы.

• Дидактические игры для повышения мотивации.

Условия реализации программы

Для реализации данной программы необходимы следующие условия:

• Кабинет с хорошей вентиляцией и качественным освещением.

• Наличие рабочих мест, соответствующих возрасту и количеству обучаемых.

• Учебная доска (функциональная при работе с мелом и магнитами).

• Аудио-видео-аппаратура.

• Канц. товары.

• Учебные пособия.

Литература и средства обучения

Литература для учителя

1. Бабкина Н.В. Нетрадиционный курс "Развивающие игры с элементами логики" для первых классов начальной школы. // Психологическое обозрение. 1996. № 2 (3), с. 47-52.

2. Зайцев Т.Г. Теоретические основы обучения решению задач в начальной

школе. - М.: Педагогика, 1983.

3. Зак А.З. 600 игровых задач для развития логического мышления детей.

Ярославль: "Академия развития", 1998.

4. Зак А.З. Развитие умственных способностей младших школьников. М.:

Просвещение, Владос, 1994.C. 48

5. Липина И. Развитие логического мышления на уроках математики //

Начальная школа. - 1999. - № 8. С. 37-39.

6. Лихтарников Л.М. Занимательные логические задачи. Для учащихся начальной школы. - СПб.: "Лань", "Мик", 2005.

7. Мельченко И.В. Примерные задания для детей, мотивированных к

интеллектуальной деятельности, в возрасте от 6 до 10 лет //

macschool.narod.ru/metod/ssm/appendix.html

8. Моро М.И., Пышкало А.И. Методика обучения математике в 1 - 3 кл. - М.:

Просвещение, 1988.

9. Муранов А.А., Муранова Н.Ф. Игры с кругами - Минск,2003.

10. Пиаже Ж. Избранные психологические труды. - СП-б: Изд-во «Питер», 1999.

11. Сухомлинский В.А. Избранные педагогические сочинения. Т. 3. М.:

Педагогика, 1981.

12. Сухин И.Г. 800 новых логических и математических головоломок. - СПб.: Альфа, 2004.

13. Формирование учебной деятельности школьников. / Под. ред. Давыдова.

В.В., Ломпшера Й., Марковой А.К. М.: Просвещение, 1999.

Литература для обучающихся

1. Зазулина Н., Цыпурский В. Занимательные игры, упражнения, задания для учащихся I-III классов. - М., 1974.

2. Арутюнян Е.Б., Левитас Г.Г. Занимательная математика: Книга для учащихся, учителей и родителей /1-5 класс. - М.: АСТ-ПРЕСС, 1999

3. Баврин И.И., Фрибус Е.А. Старинные задачи. - М.: Просвещение, 1994.

4. Сайты : vneuroka.ru/matmir/ege, logika.vobrazovanie.ru/</</u>

Приложения

Контроль и учёт знаний

по разделу

«Математика вокруг нас»

Задание 1.

Квадрат состоит из 9 различных фигур. Четыре из них раскрашены разным цветом: красным, желтым, зеленым, синим.

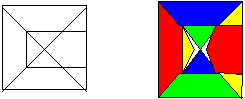
Надо раскрасить остальные фигуры этими цветами так, чтобы соседние фигуры (они имеют хотя бы одну общую точку) были раскрашены разными цветами. Известно, что желтым цветом должно быть раскрашено наибольшее число фигур.

Задание 2.

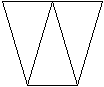
Нарисовано три одинаковых четырехугольника. Под ними написано: красный, зеленый, красный или зеленый. Надо раскрасить каждый из этих четырехугольников красным, зеленым или синим цветом так, чтобы ни одна из подписей не соответствовала действительности.

Задание 3.

1. Сколько получится, если из наименьшего двузначного числа вычесть наибольшее однозначное? (10 - 9 = 1).

2. Как сложить из 7 палочек три треугольника?

3. Как двумя отрезками разделить четырехугольник на 3 части? На 4 части?

3. Как расставить 8 стульев у четырех стен комнаты так, чтобы у каждой стены стояло по 3 стула?

Контроль и учёт знаний

по разделу

«В мире задач»

Задача 1. Знайка сказал: «Позавчера был тот же день недели, что и день сразу после субботы». В какой день недели сказал эту фразу Знайка, если он всегда говорит правду?

Задача 2. В коробке шоколадные конфеты расположены в виде квадрата в один слой. Костя съел весь первый ряд - всего 6 конфет. А Рома после этого съел весь левый ряд. Сколько конфет съел Рома?

Задача 3. Крош, Ёжик и Бараш зарыли секретики.

Крош сказал: «Я зарыл синий секретик!».

Ёжик сказал: «Нет, это Бараш зарыл синий секретик!».

А Бараш промолчал. Кто зарыл синий секретик, если синий секретик только один и все сказали неправду?

Задача 4. Посадил Дед вдоль одной тропинки три березы. Бабка между каждыми соседними березами посадила липы. А Внучка между каждыми соседними деревьями посадила по розе. Сколько роз посадила Внучка?

Задача 5. Мама купила 4 ленты красного и голубого цвета. Красных лент было больше, чем голубых. Сколько лент каждого цвета купила мама?

Задача 6. Какое наименьшее число одинаковых палочек надо взять, чтобы с помощью их составить 3 квадрата?

Контроль и учёт знаний

по разделу

«Путешествие в страну Геометрию»

Задание 1.

Соедини стрелками изображение фигуры её название.

Точка

Прямая линия

Незамкнутая кривая линия

Луч

Прямой угол

Треугольник

окружность

.

Кривая замкнутая линия

Ломаная линия

Отрезок

Тупой угол

Острый угол

Прямоугольник

Круг

квадрат

Задание 2.

Нарисуй замкнутую кривую линию, закрась цветным карандашом её внутреннюю область. Обозначь точку К , лежащую внутри этой области, точку В - вне области, точку С - на границе.

Задание 3.

Отрезок АМ длиннее, чем отрезок МТ. Отрезок МТ длиннее, чем отрезок ОК. Выполни построения.

Задание 4.

Заполни пустые клетки в квадрате , не нарушая закономерности.

Контроль и учёт знаний

по разделу

«Математика вокруг нас»

1. Пользуясь только сложением, запиши число 28 при помощи пяти двоек.

2. Сумма трёх чётных чисел равна 12. Напиши эти числа, если известно , что слагаемые не равны между собой.

____+____+_____= 12

3. Поставь между цифрами знаки «+» или «-» так, чтобы в результате получились равенства.

1 2 3 4 5 = 54

1 2 3 4 5 = 168

4. Верёвку разрезали в пяти местах. Сколько частей получилось? Обведи правильный ответ.

10 5 6 4

Контроль и учёт знаний

по разделу

«В мире задач»

1. В стакан, кружку и чашку налили молоко, простоквашу и кефир. В кружке не кефир. В чашке не кефир, и не простокваша. Что куда налили? Напиши ответ.

В кружку - _____________________________

В стакан - _____________________________

В чашку - ______________________________

2. Нарисуй , как из 4 палочек . не ломая их, получить 15?

3. У Незнайки было пять целых груш, шесть половинок да восемь четвертинок. Сколько всего груш было у Незнайки? Напиши ответ.

__________________________________

4. Портной имеет сукна на 16 м, от которого он отрезает ежедневно по 2м. По истечении скольких дней он отрежет последний кусок? Напиши ответ.

_________________________________________________

Контроль и учёт знаний

по разделу

«Путешествие в страну Геометрию»

Задание 1. Рассмотри геометрические фигуры. Раскрась те многоугольники, у которых есть хотя бы один прямой угол.

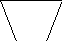
Задание 2. Определи, на сколько нужно увеличить каждую сторону квадрата, чтобы его периметр увеличился на 32 см

_____________________________________________

Ответ: ________________________________________

Задание 3. Начерти квадрат такой же площади, как прямоугольник со сторонами 2 см и 8 см. Найди периметр квадрата.

Контроль и учёт знаний

по разделу

«Математика вокруг нас»

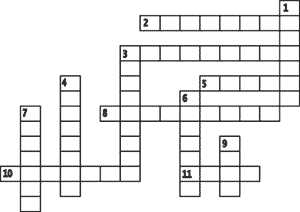
По горизонтали: 2. Математическое действие. 3. Какое математическое действие нужно выполнить, чтобы найти произведение? 5. Промежуток времени в 24 часа. 8. Число, которое умножается на другое. 10. Результат деления. 11. Единица измерения объема жидкости.

По вертикали: 1. Математическое действие. 3. Равенство с одним неизвестным. 4. Сумма длин всех сторон. 6. Прибор для построения окружности. 7. Произведение длины на ширину прямоугольника. 9. Единица длины.

Контроль и учёт знаний по разделу «В мире задач»Задача 1. Верные друзья

Пятачок хочет вставить в три разные рамки портреты Винни-Пуха, Тигры и Иа-Иа. Он может разместить портрет Винни-Пуха в розовой рамочке, Тигры - бирюзовой, а Иа-Иа - в коричневой. А сколько всего разных способов есть у Пятачка, чтобы разместить портреты своих друзей ?

a) 1 способ b) 2 способа; c) 3 способа; d) 4 способов; e) 5 способов; f) 6 способов;

Задача 2. Конфеты и логика

Мой дедушка очень любит розыгрыши. Он закрыл дверь комнаты, где моя бабушка хранит конфеты, на ключ. Ключ он положил в одну из коробочек, которые он замаркировал так: А, Б, В.

Затем он прикрепил записочки к каждой коробочке:

А) Ключ не в коробке Б

Б) Ключ не в этой коробке

В) Ключ в этой коробке

Бабушка сказала мне, что некоторые из этих утверждений правильные, а некоторые - ложные.

Но если, не заглядывая в коробочки, я протяну дедушке коробочку, в которой будет лежать ключ, у меня будет столько конфет, сколько я захочу.

Какую коробочку надо протянуть дедушке ?

(a) А; (b) Б; (c) В; (d) Невозможно определить.

Задача 3. Улитка поднимается вверх

Улитка за 2 мин. проползает по грибу 2 см вверх. Затем 1 мин. отдыхает и моментально соскальзывает вниз на 1 см.

После этого она снова начинает подниматься вверх все в той же манере.

На какой высоте она будет через 5 минут?

(a) 2 см; (b) 3 см; (c) 4 см; (d) 5 см;

Задача 4. Погонщики верблюдов

Одно и двугорбые верблюды пересекают пустыню. У всех у них 14 горбов и 40 ног.

На каждом втором двугорбом верблюде сидит погонщик.

Сколько всего погонщиков путешествуют вместе с верблюдами ?

a) 1 погонщик ; b) 2 погонщика; c) 3 погонщика; d) 4 погонщика; e) 5 погонщиков;

Контроль и учёт знаний

по разделу

«Путешествие в страну Геометрию»

1. Начерти прямоугольник, площадь которого 12 см², а сумма длин сторон 26см.

2. Сколько требуется проволоки, чтобы изготовить каркас куба с ребром 7см?

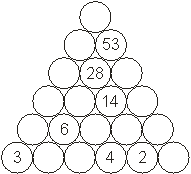
3. В этой фигуре сумма двух соседних кругов равна кругу лежащему над ними. Впишите цифры и числа в свободные круги, соблюдая симметрию в каждой строчке.

4. Считаем ступеньки Сережа поднимается по лестнице. Каждый раз он перепрыгивает через одну ступеньку.

Сейчас он - на третьей ступеньке.

На какой ступеньке он окажется, сделав три своих "шага"?

Если вы уже посчитали, поищите свое число в списке ответов :

(a) 9; (b) 8; (c) 6; (d) 5;

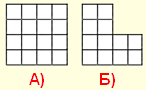
5. Посчитаем квадратики

На рисунке А можно увидеть больше квадратиков, чем на рисунке Б. На сколько ?

(a) 1; (b) 4; (c) 5; (d) 8; (e) 10; (f) 13;

Контроль и учёт знаний

по разделу

«Математика вокруг нас»

1.Расставь скобки так, чтобы получились верные равенства.

12 * 16 + 128 : 8 + 24 = 240

12 * 16 + 128 : 8 + 24 = 196

12 * 16 + 128 : 8 + 24 = 323

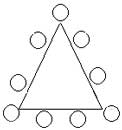
2. Расставить вдоль сторон треугольника цифры 1, 2, 3,..., 9 так, чтобы сумма цифр вдоль каждой стороны равнялась 20-ти. Цифра, стоящая в вершине треугольника, принадлежит каждой из сторон, выходящих из этой вершины.

3. Шестизначное число оканчивается цифрой 4. Если эту цифру переставить из конца числа в начало, т.е. приписать ее перед первой, не изменяя порядка остальных пяти, то получится число, которое в 4 раза больше первоначального. Найдите это число.

4. Не меняя порядка расположения чисел, поставьте между ними математические знаки (+, -, х, :) так, чтобы в результате этих действий в каждом ряду получился ответ 1. Если понадобится, две рядом стоящие цифры превращайте в двузначные числа. Можно применять скобки.

1 2 3 =1

1 2 3 4 =1

1 2 3 4 5 =1

Контроль и учёт знаний

по разделу

«В мире задач»

1. Попрыгунья - Стрекоза половину времени каждых суток красного лета спала, третью часть времени каждых суток - танцевала, шестую часть - пела. Остальное время она решила посвятить подготовке к зиме. Сколько часов в сутки Стрекоза готовилась к зиме?

2. Поставили подряд 8 мешков. Вес первого мешка - 88 кг, а вес каждого следующего - на 8 кг меньше предыдущего. Найди массу всех мешков.

3. Расстояние от города А до города Б 32 км, а от А до С - 40 км, от Б до С - 28 км. Выполни чертеж. Курьер находится в городе А, но ему надо посетить города Б и С, не возвращаясь назад в город А. Какой наикратчайший путь ему выбрать?

4. Из куска проволоки согнули квадрат, S которого 36 см кв. Затем проволоку разогнули и согнули из неё треугольник с равными сторонами. Какова длина сторон треугольника?

5. Петя собирал в саду яблоки. 6 яблок, что составило десятую часть собранного, он положил в карман, остальные высыпал в корзину. Сколько яблок в корзине?

6. Сумма двух чисел равна 462. Одно из них оканчивается нулём. Если этот нуль зачеркнуть, то получится второе число. Найди эти числа.

7. По тропинке вдоль кустов шло 11 хвостов. Насчитать я также смог, что шагало 30 ног. Это вместе шли куда-то индюки и жеребята. А теперь вопрос таков: сколько было индюков?

8. В семье четверо детей: им 5. 8, 13 и 15 лет, а зовут их Таня, Юра, Света, Лена. Сколько лет каждому из них, если одна девочка ходит в детский сад, Таня старше, чем Юра, а сумма лет Тани и Светы делится на 3?

Контроль и учёт знаний

по разделу

«Путешествие в страну Геометрию»

Задача 1. Геометрия на шахматной доске

У нас была квадратная доска, подобная шахматной. На каждую клетку по краям этой доски и на каждую клетку одной из диагоналей мы поставили по одной шахматной фигуре.

Нам для этого понадобилось 64 фигуры.

Сколько пустых клеток все еще осталось на этой доске ?

(a) 132; (b) 196; (c) 208; (d) 225;

Задача 2 . Шоколад и Поварята

Пять Маленьких Поварят решили разделить между собой большую прямоугольную шоколадку.

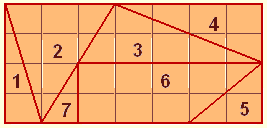
Но она упала на пол и когда они развернули ее, то увидели, что шоколадка разбилась на 7 кусков. Николай съел самый большой кусок. Света и Маша съели одно и тоже количество шоколада, но Света съела три куска, а Маша только один кусок. Белла съела 1/7 часть целой шоколадки, и Катя съела все остальное. Какой кусок шоколадки достался Кате ?

(a) 1; (b) 2; (c) 3; (d) 4; (e) 5; (f) 7;