Үшбұрыш және трапецияның орта сызығы қмж

Күні: 11.11.2016 Тексерілді 11.11.2016

Сыныбы: 8 «Б» ____________________

Пәні: Геометрия

Сабақ тақырыбы: Үшбұрыштың және трапецияның орта сызықтары

Сабақ мақсаты: Теоремаларды дәлелдеу арқылы үшбұрыш және трапецияның орта сызықтарын табуды үйрену, тақырыптың мазмұнын игеру арқылы, топпен талқылау арқылы ойын толық жеткізіп сөйлеу дағдылары мен жазбаша тілдерін жетілдіруге дағдыланады.

Күтілетін нәтиже: Оқушылар тақырыппен жұмыс істеу тәсілдерін еркін пайдаланады, түсінеді және тапсырмаларды қатесіз орындайды, тақырыппен жұмыс жасау арқылы танымдық қабілеттерін арттырады

Сабақ әдісі: «Жұптық жұмыс», «Топтық жұмыс», «Жеке жұмыс», «Джигсо», «Деңгейлік тапсырмалар», «Досыма хат»

Пайдаланған дереккөздер мен ресурстар: И. Бекбонв геометрия 8 Алматы «Мектеп» 2008, Погорелов 7-11 Алматы «Мектеп» 2001ж, Бейсеков Ж «Планиметриядан есептерді шығаруға арналған әдістемелік құрал» Шыныбеков Геометрия 8 Алматы «Мектеп» 2004, www.ustaz.kz, www.youtube.com , www.google.kz, сызғыш, циркуль, интербелсенді тақта, плакат.

Кіріспе

2 мин

Ынтымақтастық атмосферасын қалыптастыру

Шаттық шеңберінде математикалық тілде тілек айтады

2 мин

Топтарға бірігу

Оқушылар стикерлер арқылы 4 топқа бөлінеді

6 мин

Жұптық жұмыс жасау арқылы үй тапсырмасын тексеру

Интербелсенді тақтада дұрыс жауаптары шығады

Критериалды бағалау

«5» - Егер 2 есептің де шешу жолдары дұрыс, сызбасы бар, жауабы дұрыс болса

«4» - Егер есептердің шешу жолдарының біреуі болмаса, немесе сызбасы сызылмаса бірақ жауабы дұрыс болса.

«3» - Егер 2 есептің де шешу жолдары дұрыс, сызбасы бар, бірақ жауабы дұрыс болмаса

«2» - Егер 2 есептің де шешу жолдары дұрыс болмаса, сызбасы жоқ, жауабы қате болса

№70 Берілгені: Шешуі:

ABCD - тең бүйірлі AB=CD=10 см

Трапеция BC=EF=8 см

BC=8 см ⁰;

AB=10 см AE=FD=AB/2=10 см/2=5 см

⁰ AD=AE+EF+FD=

Т/к P_ABCD =5 см+8 см+5 см=18 см

P_ABCD=AB+BC+CD+AD=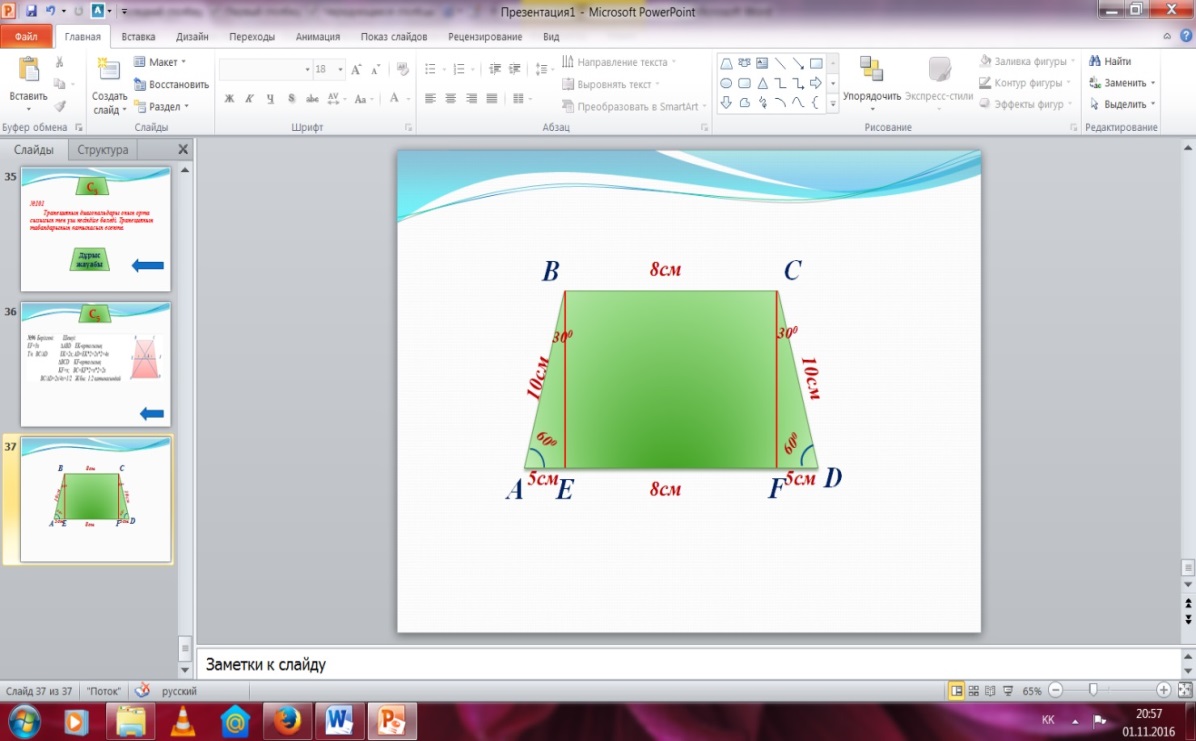

=10 см+8 см+10 см+18 см=46 см

Ж/бы: 46 см

№71 Берілгені: Шешуі:

ABCD - тең бүйірлі

=56⁰ +<С=y

Т/к </</i>D

2x=236 x=118⁰

118⁰ +y=180⁰

y=62⁰

Ж/бы: 118⁰ ; 62⁰; 118⁰; 62⁰;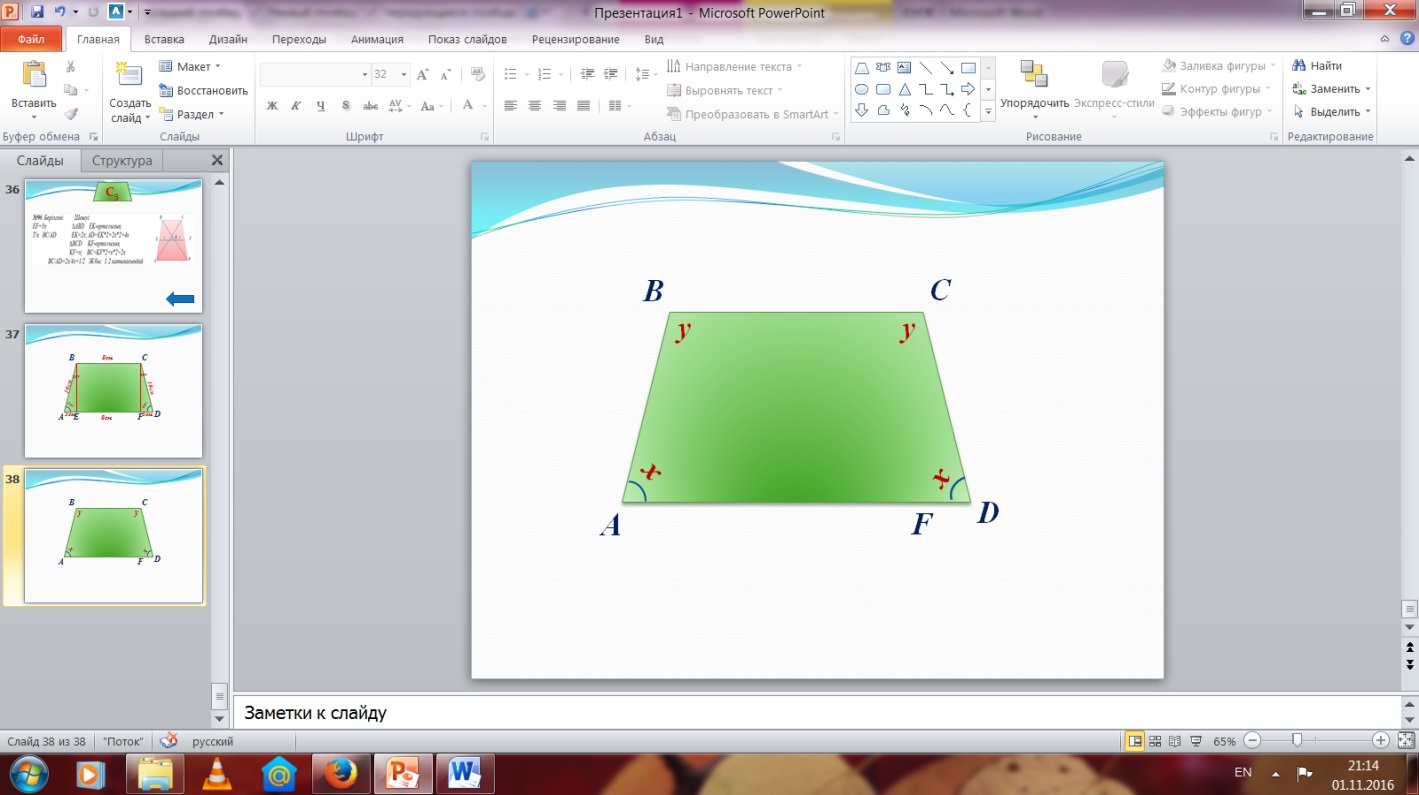

Таныстырылым

4 мин

Бейнебаян арқылы тақырып мағынасын ашу

Түсінгендерін айтады

Термин сөздердің қазақшасын жазады.

Бас бармақ

What is a triangle?

One of the three points is not a straight line, and points to a figure called a triangle of strokes that.

Қолдану

7 мин

Постер қорғау арқылы теоремаларды дәлелдеу

Теоремаларды 2 бөлікке бөліп дәлелдейді.

2 жұлдыз

1 тілек

Теорема 1. Үшбұрыштың екі қабырғасының ортасын қосатын орта сызық үшінші қабырғаға параллель және оның жартысына тең.

Дәлелдеу(1 бөлігі)АВС үшбұрыш берілсін.DЕорта сызығын жүргізіп, DЕ║АВ болатынын дәлелдейміз.

DЕ сәулесінің бойына Е нүктесінен әрі жалғастырып ЕF=DE кесіндісін өлшеп саламыз. Сонда ∆CED=∆BEF болады. Үшбұрыштар теңдігінің бірінші белгісі бойынша. Бұл жерде EF=DE, CE=BE және <1 = <2 вертикаль бұрыштар. Бұдан DC=BF (1) және <3 = <4 (2). Сондықтан AD=DC=BF (3) Айқыш бұрыштардың теңдігінен, яғни (2)-ден DС║BF немесе AD║BF шығады. (4) Сонда (3)пен (4) - тен ABFD төртбұрышы параллелограмм болып тұр. Олай болса, DЕ║АВ

(2 бөлігі) DF=AB болғандықтан, Е нүктесі DF кесіндісінің қақ ортасын болғандықтан DE= болады. Теорема дәлелденді.

Теорема 2. Трапецияның орта сызығы табандарына параллель және табандарының қосындысының жартысына тең.

Дәлелдеу. (1 - бөлігі) ABCD трапециясы берілген болсын. EF орта сызығы болсын. ЕF║АВ, ЕF║DC болатынын дәлелдейміз.

AD бүйір қабырғасының ортасы Е нүктесі арқылы AB және DC табандарына параллель түзу жүргізсек, ол ВС бүйірін F нүктесінде қиып отеді. AE=ED болғандықтан, Фалес теоремасы бойынша BF=FC. Олай болса, EF - трапецияның орта сызығы. Өзіміздің сұрауымыз бойынша, ЕF║АВ, ЕF║DC. Демек, теореманың бірінші бөлігі дәлелденді.

Трапецияның BD диагоналін жүргізсек Фалес теоремасы бойынша О нүктесі BD кесіндісінің ортасы болады. Ендеше, FO және OF кесінділері сәйкесінде ABD, BCD үшбұрыштарының орта сызықтары: оларды қоссақ, аламыз. Теореманың 2 - бөлігі дәлелденді.

8 мин

Оқулықпен жұмыс.

№77 - №98 есептерді шығару

Деңгейлік тапсырмалар. Әр оқушы өз деңгейіне қарай отырып интербелсенді тақтадағы есептерді таңдап шығарады.

Критериалды бағалау

№77

1. Берілгені: Шешуі:

АВС - үшбұрыш

АВ=12дм

Т/к EF-? Ж/бы: 6 дм

«5» - Егер есептің шешу жолдары дұрыс, сызбасы бар, жауабы дұрыс болса

«4» - Егер есептердің шешу жолдарының біреуі болмаса, немесе сызбасы сызылмаса бірақ жауабы дұрыс болса.

«3» - Егер 2 есептің де шешу жолдары дұрыс, сызбасы бар, бірақ жауабы дұрыс болмаса

«2» - Егер 2 есептің де шешу жолдары дұрыс болмаса, сызбасы жоқ, жауабы қате болса

№77

2. Берілгені: Шешуі:

АВС - үшбұрыш

EF=4.5 см AB=2EF=2*4.5=9см

Т/к AB-? Ж/бы: 9см

№78 Берілгені: Шешуі:

АВ=6м

BC=9м

AC=13м

Т/к DE, EF, FD - ? Ж/бы: 6,5м; 3м; 4,5м;

№79 Берілгені: Шешуі:

DE=5дм AB=EF*2=7*2=14дм

EF=7дм BC=FD*2=10*2=20дм

FD=10дм AC=DE*2=5*2=10дм

Т/к AB, BC, AC - ? Ж/бы: 14дм; 20дм; 10дм;

№80 Берілгені Шешуі

Ж/бы: 12м

№81 Берілгені Шешуі

P₁ =2P₂=2*15дм=30дм Ж/бы: 30дм

№83 Берілгені Шешуі

AB=4x P_ABC= P_DEF*2=3.6дм*2=7.2дм

BC=3x 4x+3x+5x=7.2

AC=5x 12x=7.2 x=0.6

P_DEF=3.6 дм AB=4*0.6=2.4дм

Т/к x-? BC=3*0.6=1.8дм

AC=5*0.6=3дм Ж/бы: 2,4 дм; 1,8 дм; 3 дм;

№84 Берілгені Шешуі: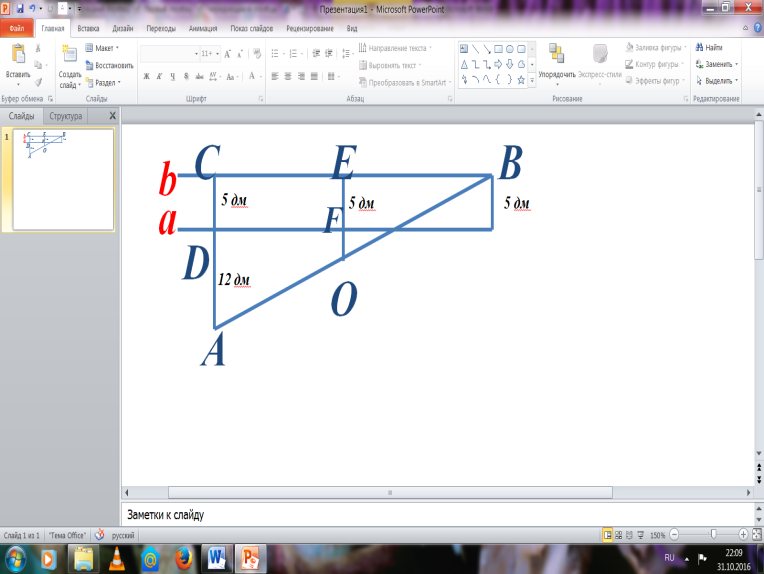

AD=12 дм BE=EF=CD=5дм

BE=5 дм AC=AD+DC=17 дм

Т/к OF - ? ∆ABC үшбұрыш

EO - орта сызық

OF=8.5-5=3.5дм Ж/бы: 3,5 дм

№88 Берілгені Шешуі: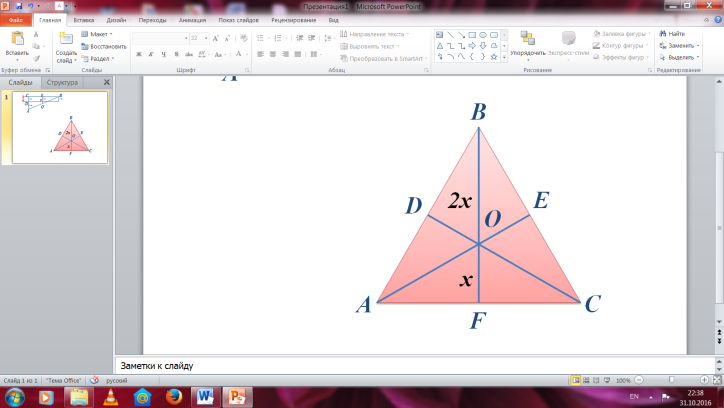

∆ABC үшбұрыш BO=2x

BF=6 м OF=x

т/к BO, OF-? 2x+x=6

3x=6 x=2

OF=2м, BO=2*2м=4м Ж/бы: 2м; 4м;

№91 Берілгені : Шешуі: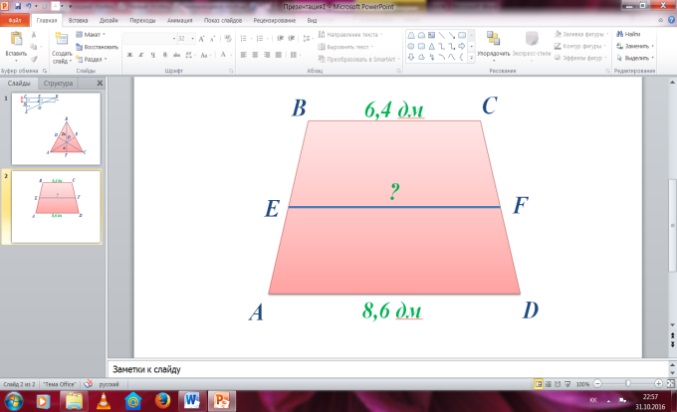

ABCD - трапеция

BC=6.4дм

AD=8.6 дм Ж/бы: 7,5 дм

Т/к EF - ?

№92 Берілгені: Шешуі: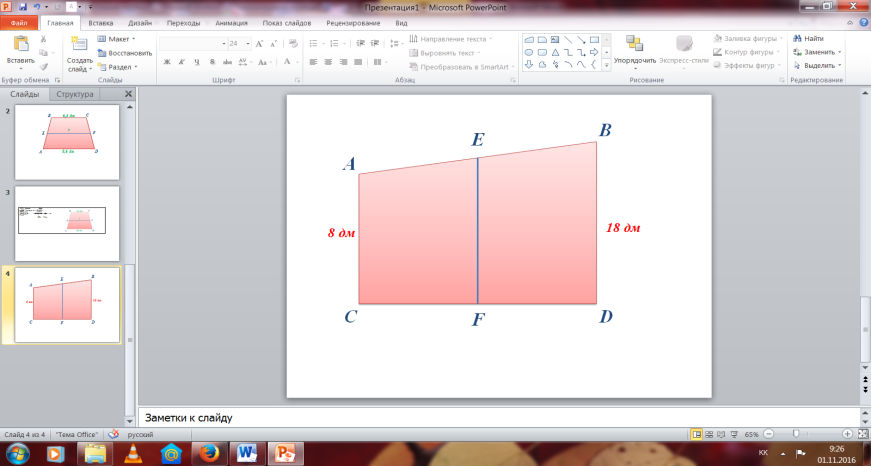

1. Жағдай

AC=8 дм

BD=18 дм Ж/бы: 13 дм

Т/к EF - ?

2. Жағдай Шешуі:

Берілгені AF=KB=8 дм

AE=18 дм EF=AE+AF=18 дм+8 дм=26 дм

KB=8 дм OL=EF/2=26/2=13 дм

Т/к OD - ? OD=OL-DL=13 дм-8 дм=5 дм Ж/бы: 5 дм

№93 Берілгені: Шешуі: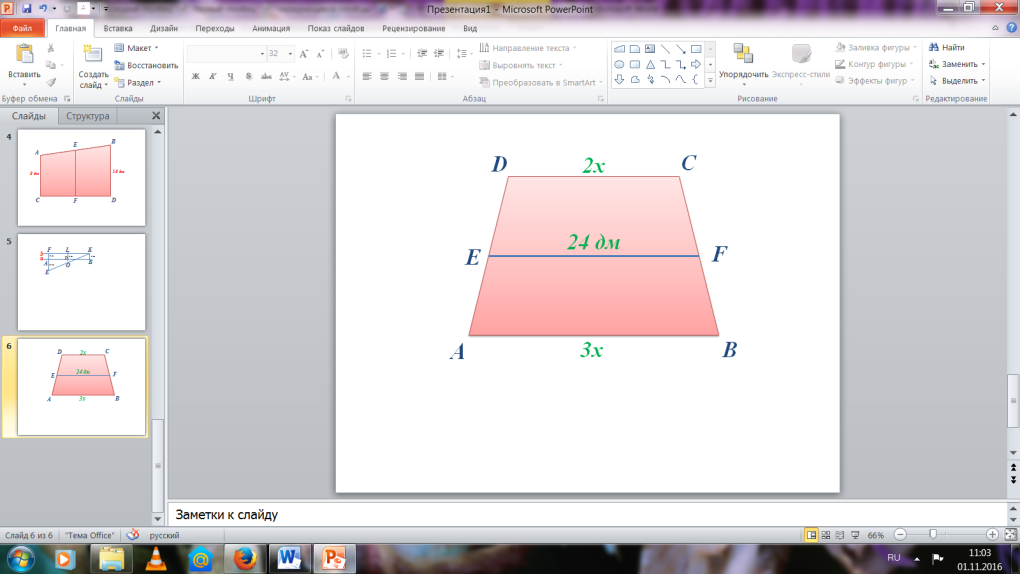

DC=2x EF=(DC+AB)/2

AB=3x (2x+3x)/2=24 дм

EF=24 дм 5x/2=24

Т/к DC, AB - ? 5x=48 x=9.6

DC=2*9.6=19.2 дм

AB=3*9.6=28.8 дм

Ж/бы: 19,2 дм; 28,8 дм

№95 Берілгені: Шешуі: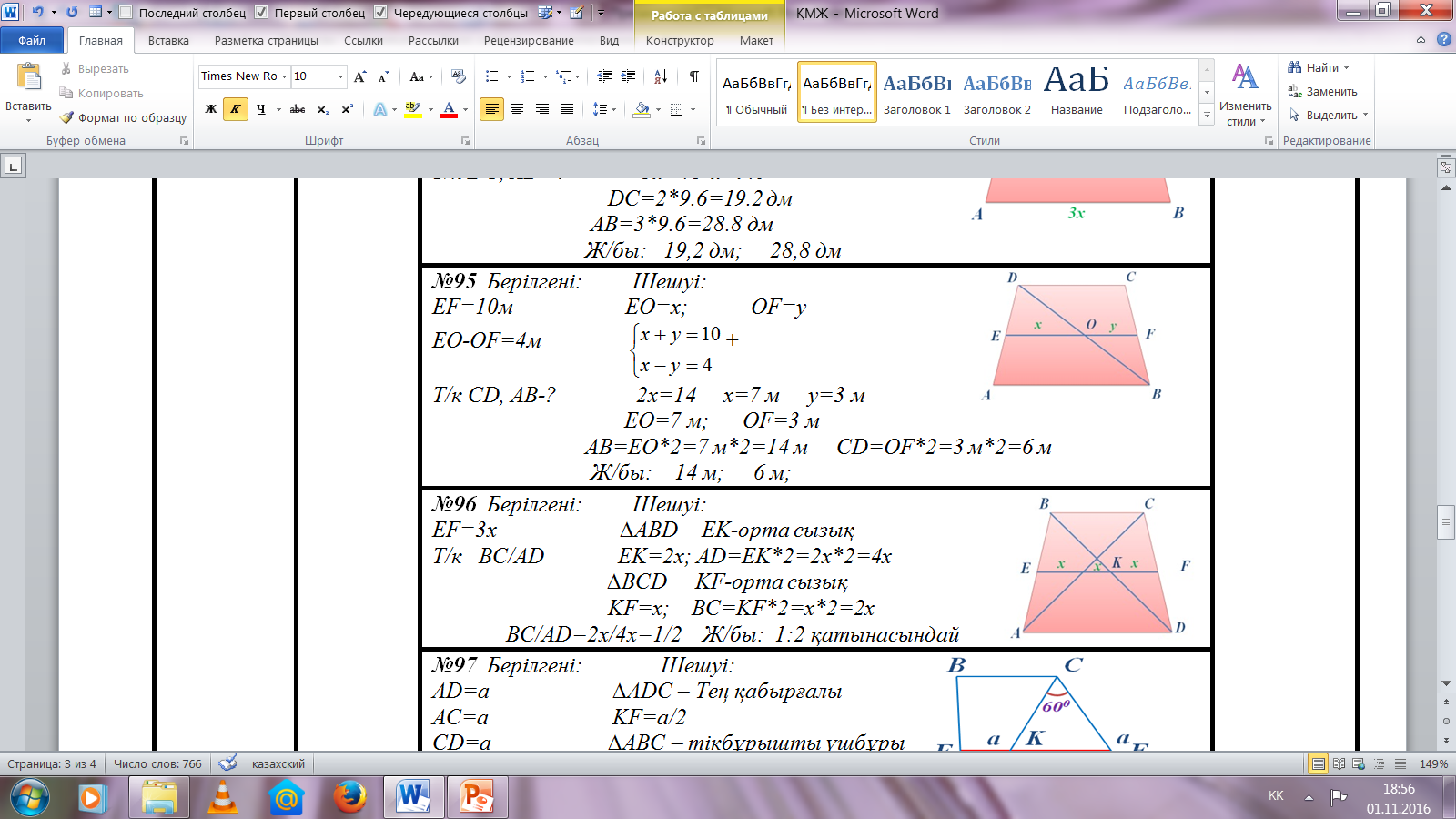

EF=10м EO=x; OF=y

EO-OF=4м +

Т/к CD, AB-? 2x=14 x=7 м y=3 м

EO=7 м; OF=3 м

AB=EO*2=7 м*2=14 м CD=OF*2=3 м*2=6 м

Ж/бы: 14 м; 6 м;

№96 Берілгені: Шешуі:

EF=3x ∆ABD EK-орта сызық

Т/к BC/AD EK=2x; AD=EK*2=2x*2=4x

∆BCD KF-орта сызық

KF=x; BC=KF*2=x*2=2x

BC/AD=2x/4x=1/2 Ж/бы: 1:2 қатынасындай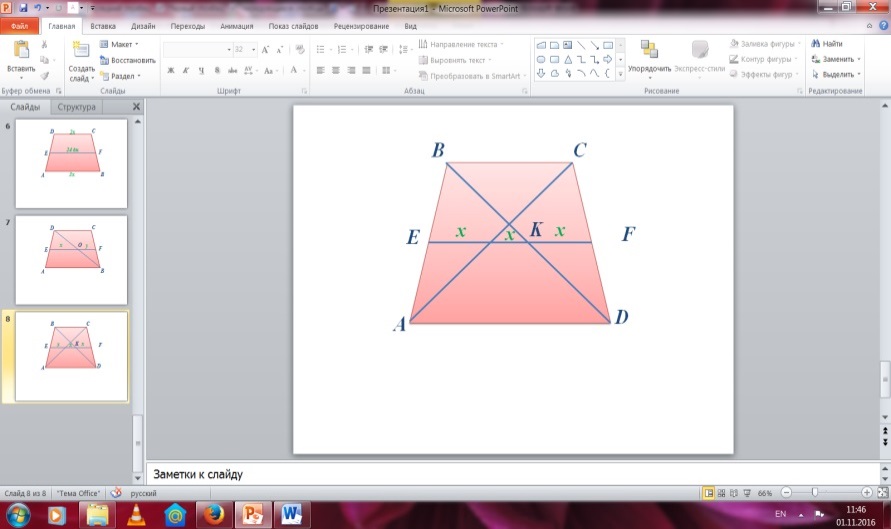

№97 Берілгені: Шешуі: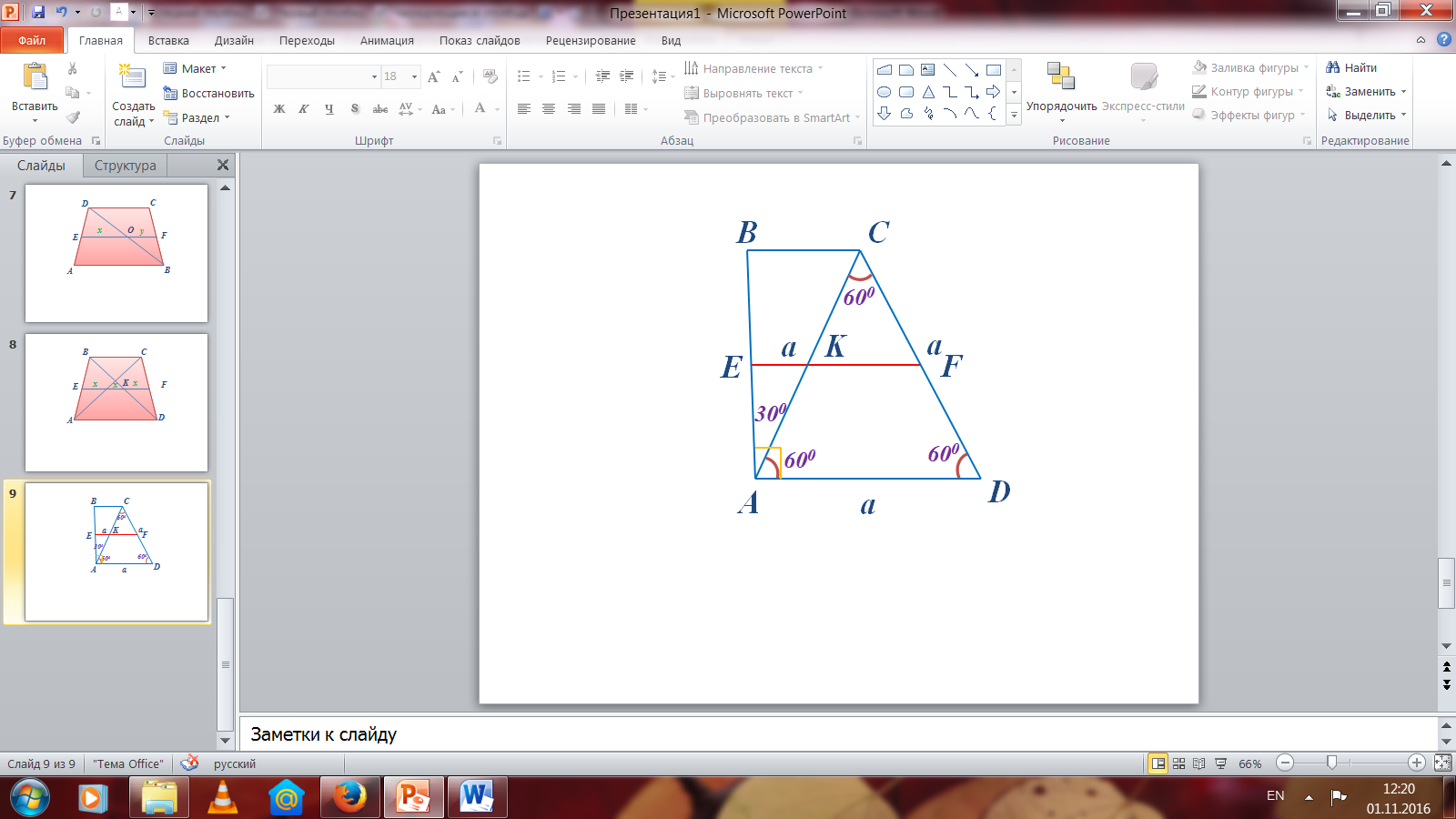

AD=a ∆ADC - Тең қабырғалы

AC=a KF=a/2

CD=a ∆ABC - тікбұрышты үшбұрыш

Т/к EF-? BC=AC/2=a/2

EK=a/2:2=a/4

EF=EK+KF=a/2+a/4=3a/4

Ж/бы: 3а/4

№101 Берілгені: Шешуі: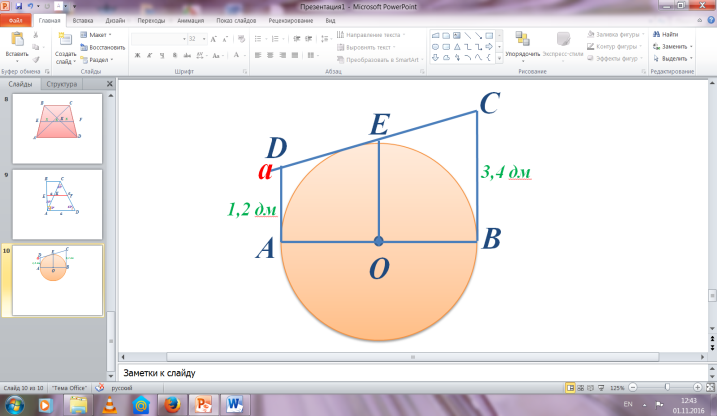

AD=1.2 дм ABCD - трапеция

BC=3.4 дм EO - орта сызық,

Т/к AB-? шеңбердің радиусы

EO=(AD+BC)/2=(1.2 дм +3.4 дм)/2=

=4.6 дм /2=2.3 дм

AB=EO*2=2.3 дм*2=4.6 дм

Ж/бы: 4,6 дм

№6 Берілгені: Шешуі: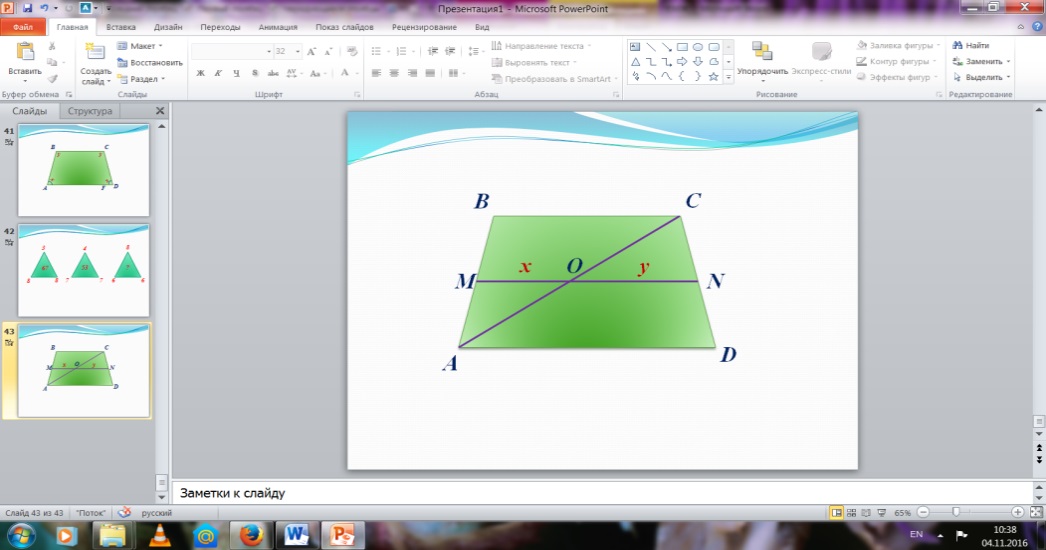

ABCD трапеция, BC║AD ∆ABC - нан:

BC=4cм, AD=10 cм x=BC/2=4/2=2 cм

Т/к: x-? y-? ∆ACD - нан:

y=AD/2=10/2=5 cм

Ж/бы: 2 cм; 5 cм;

Қорытынды

7 мин

Жеке жұмыс

Оқушыларға үшбұрыштың және трапецияның пішіндері беріледі.

Қабырғаларын сызғышпен өлшеп олардың орта сызықтарын табады.

Бірін - бірі бағалайды

3 мин

Сергіту сәті.

Логикалық тапсырмалар

«Тест на психику»

Логикалық сұрақтарға жауап береді.

Ынталандыру

4 мин

Жаңа тақырыпты «Досыма хат» әдісі бойынша пысықтау

Сабақта алған білімдерін параққа қысқаша жазып бір бірімен алмасады.

Бас бармақ

1 мин

Рефлекция

Стикерге жазып үміт ағашына жапыстырады

1 мин

Үйге №99 - №100 есептерді шығаруға және әр түрлі пішінде үшбұрыш және трапеция жасап келуге нұсқау беру.

Күнделіктеріне жазып алады.

Ұпайды мектеп бағасына айналдыру шкаласы

Баға

Ұпайлар

2

0-1 - «2»

3

2-3 - «3»

4

4-5 - «4»

5

6-7 - «5»

Ең жоғары ұпай саны - 7

5 ұпайлық шкаладағы бағаның сипаты

5 ұпай - үздік

4 ұпай - жақсы

3 ұпай - қанағаттандырылған

2 ұпай - қанағатсыздандырылған