- Учителю
- Контрольная работа в 10 классе
Контрольная работа в 10 классе
Вариант 1.
1. В прямоугольном параллелепипеде ![]() известно, что
известно, что ![]()
![]()
![]() Найдите длину ребра
Найдите длину ребра ![]() .
.
2. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота - 2
3. В правильной четырехугольной пирамиде ![]() точка
точка ![]() - центр основания,
- центр основания, ![]() - вершина,
- вершина, ![]() ,
, ![]() . Найдите боковое ребро
. Найдите боковое ребро ![]() .
.
4. В правильной треугольной пирамиде ![]() точка
точка ![]() - середина ребра
- середина ребра ![]() ,
, ![]() - вершина. Известно, что
- вершина. Известно, что ![]() =3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка
=3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка ![]() .
.
Вариант 2.
1.В прямоугольном параллелепипеде ![]() известно, что
известно, что ![]()
![]()
![]() Найдите длину ребра
Найдите длину ребра ![]() .
.
2.Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
3. В правильной четырехугольной пирамиде ![]() точка
точка ![]() - центр основания,
- центр основания, ![]() - вершина,
- вершина, ![]()
![]() Найдите длину отрезка
Найдите длину отрезка ![]() .
.
4. В правильной треугольной пирамиде SABC точка L - середина ребра AC, S - вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
Вариант 3.
1. В прямоугольном параллелепипеде ABCDA1B1C1D1 D1В = 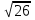 , ВВ1 = 3, А1D1 = 4. Найдите длину ребра А1В1.
, ВВ1 = 3, А1D1 = 4. Найдите длину ребра А1В1.
2. В правильной четырехугольной пирамиде SABCD точка О - центр основания, S - вершина, SO = 10, BD = 48. Найдите боковое ребро SA.
3. В правильной треугольной пирамиде SABC М - середина ребра АВ, S - вершина, ВС = 4, SМ = 3. Найдите площадь боковой поверхности пирамиды.
4. Площадь поверхности куба равна 200. Найдите его диагональ.
Вариант 4.
.
1.. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 32 и 42. Площадь поверхности параллелепипеда равна 6240. Найдите его диагональ.
2. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 40, и боковым ребром, равным 55.
3. В правильной четырехугольной пирамиде ![]() точка
точка ![]() - центр основания,
- центр основания, ![]() - вершина,
- вершина, ![]() ,
, ![]() . Найдите боковое ребро
. Найдите боковое ребро ![]() .
.
4. В правильной треугольной пирамиде ![]() точка
точка ![]() - середина ребра
- середина ребра ![]() ,
, ![]() - вершина. Известно, что
- вершина. Известно, что ![]() =3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка
=3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка ![]() .
.
Вариант 5.
1. В прямоугольном параллелепипеде ![]() известно, что
известно, что ![]()
![]()
![]() Найдите длину ребра
Найдите длину ребра ![]() .
.
2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
3. В правильной четырехугольной пирамиде ![]() точка
точка ![]() - центр основания,
- центр основания, ![]() - вершина,
- вершина, ![]() =12,
=12, ![]() =18. Найдите боковое ребро
=18. Найдите боковое ребро ![]()
4. В правильной треугольной пирамиде SABC точка L - середина ребра AC, S - вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
Вариант6.
1. В прямоугольном параллелепипеде ABCDA1B1C1D1 С1А = 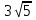 , СС1 = 2, А1D1 = 5. Найдите длину ребра CD.
, СС1 = 2, А1D1 = 5. Найдите длину ребра CD.
2. В правильной четырехугольной пирамиде SABCD точка О - центр основания, S - вершина, SD = 13, BD = 10. Найдите длину отрезка SО.
3. В правильной треугольной пирамиде SABC К - середина ребра СВ, S - вершина, ВА = 6, а площадь боковой поверхности равна 63. Найдите длину отрезка SК.
4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 5 и 12, и боковым ребром, равным 17.
Вариант 7.
1. В прямоугольном параллелепипеде ABCDA1B1C1D1 АС1 = 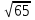 , DD1 = 5, В1С1 = 6. Найдите длину ребра D1C1.
, DD1 = 5, В1С1 = 6. Найдите длину ребра D1C1.
2. В правильной четырехугольной пирамиде SABCD точка О - центр основания, S - вершина, SO = 7, АС = 48. Найдите боковое ребро SВ.
3. В правильной треугольной пирамиде SABC Р - середина ребра ВС, S - вершина, АВ = 7, SР = 16. Найдите площадь боковой поверхности пирамиды.
4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 5 и 12, и боковым ребром, равным 16.
Вариант 8.
1. Найдите квадрат расстояния между вершинами C и A1прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 12. Площадь поверхности параллелепипеда равна 576. Найдите его диагональ.
3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
4. Высота правильной треугольной пирамиды равна 2√3, радиус окружности, описанной около её основания, 4. Найдите а) апофему пирамиды; б) угол между боковой гранью и основанием; в) площадь боковой поверхности; г) плоский угол при вершине пирамиды.