Урок- исследование Геометрические задачи практического содержания (8-9 класс)

ОТКРЫТЫЙ УРОК-ИССЛЕДОВАНИЕ В 9 КЛАССЕ

Тема. Повторение. Геометрические задачи практического содержания

Цель урока:

Образовательный аспект:

• показать многообразие подходов к решению одной задачи,

• формировать умение видеть рациональные способы решения,

• создать условия для повторения и систематизации знаний учащихся по темам «Признаки подобия», «Прямоугольные треугольники»,

• разработать модель решения геометрических задач практического содержания из вариантов ГИА 9 класса,

• закрепить умения и навыки использования признаков подобия при решении различных геометрических задач практического содержания,

• исследовать способы решения задач практического содержания,

• показать красоту и значимость геометрии.

Развивающий аспект:

• создать условия для индивидуализации обучения и саморазвития учащихся,

• развивать навыки исследовательской деятельности,

• развивать умения учебного труда;

• развивать познавательные процессы: память, воображение, мышление, внимание, наблюдательность, сообразительность;

• развивать способность к оценке своей работы и работы товарища;

• повысить интерес учащихся к решению нестандартных задач;

• формировать культуру речи;

Воспитательный аспект:

• создать у учащихся положительную мотивацию к изучению математики путем вовлечения каждого ученика в активную познавательную деятельность;

• создать условия для воспитания коммуникативных качеств учащихся;

• воспитывать ответственность учащихся за результаты обучения;

• воспитывать личностные качества: воля, самостоятельность, ответственность.

Методы: творческо-поисковый, исследовательский

Оборудование: проектор, компьютер, демонстрационные рисунки, раздаточный материал (карточки с заданиями), мел, доска.

Формы работы: самостоятельная работа в парах, фронтальная работа, индивидуальная работа.

План урока:

1.Организационный момент

2.Теоретический опрос в виде теста к №13 экз. материалов по темам а) признаки подобия треугольников, б) пропорциональные отрезки, в) прямоугольные треугольники

3.Выступление учащихся о различных способах решения одной задачи, презентация, заполнение сравнительной таблицы

4.Работа в парах: анализ сравнительной таблицы, подведение итогов сравнительной таблицы, решение задачи по прототипу №17 КИМов

ХОД УРОКА

1. Слово учителя о цели этого урока

Эпиграф

На свете столь много подобных вещей.

Наш мозг перестал удивляться!

Исследовать суть, разобрать, обобщить…

По-моему, стоит пытаться.

И на уроке сейчас повторим

Проблему, не глядя в пособие.

Из КИМов задачу успешно решим,

Используя свойства подобия.

Цель

Рассмотрим стандартную задачу из КИМов ГИА, решим ее различными способами, проанализируем и выберем наиболее оптимальные способы

На уроке будет рассмотрена задача практического содержания, решить которую помогут приобретенные геометрические знания. Поэтому наш урок является уроком повторения: повторяются темы: «Признаки подобия», «Прямоугольные треугольники». Все предлагаемые задания являются прототипами заданий №13 и №17 экзаменационного теста.

Повторение теории проведем в форме устного тестирования, решим задачу практического содержания несколькими способами, исследуем представленные способы, а в конце урока произведём анализ полученных результатов.

2. Устный тест (5 минут)

(Признаки подобия треугольников, пропорциональные отрезки, прямоугольные треугольники)

1. Какие из следующих утверждений верны?

1)Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

2)Любые два равнобедренных треугольника подобны.

3)Равенство двух отношений называется пропорцией. 4)Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

5)Отношение площадей подобных треугольников равно их коэффициенту подобия.

6) Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. 7)Любые два равносторонних треугольника подобны. 8)Если острый угол одного прямоугольного треугольника равен углу другого прямоугольного треугольника, то такие треугольники равны. 9)Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Таблица ответов: (134679)

3. Презентация и оформление решения задач в тетрадях. Проводят ученики1.Человек ростом 1,8 м видит верхушку дерева и край крыши дома. Высота дерева 3,6 м, расстояние от человека до дерева 3,6 м, от дерева до дома 7 м. Определите высоту дома (в метрах).

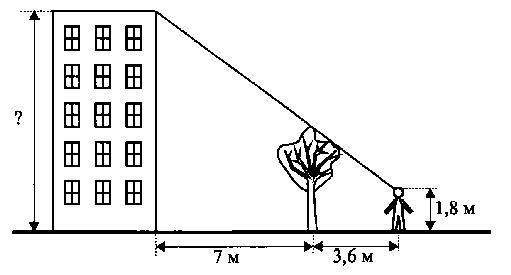
Исходные данные:

Рост человека - 1,8 м, высота дерева - 3,6 м, расстояние от человека до дерева - 3,6 м, от дерева до дома 7 м.

Результат:

Высота дома (в метрах).

!!!!!!!!

Перед каждым из вас лежит бланк отчета для анализа представленных решений. Во время очередного выступления вносите информацию в соответствующие колонки, а в конце просуммируйте «плюсы» по строкам. Сделайте вывод о самом оптимальном для вас решении. Подумайте об актуальности темы сегодняшнего урока. Ответьте, зачем надо искать различные способы решения одной задачи, не лучше ли было решить за это время несколько различных задач.

Создание математи-

ческой модели

Дано: AC CN, KM CN, LN CN; LN=1,8 м; KM=3,6 м; MN=3,6 м; CM=7 м.

Найти: AС

Вычисли-тельный этап

1 способ «Подобие»

Теоретический минимум:

Первый признак подобия треугольников (по двум углам).

Длина отрезка равна сумме длин частей, из которых состоит этот отрезок.

Решение:

1) Д.П. найдём точку пересечения прямых АL и СN. Получим точку В. Пусть NB=x м, тогда MB=(3,6+x) м

2)ΔMKB~ΔNLB (по двум углам).

2) ΔCAB~ΔNLB (по двум углам).

Ответ: м

2 cпособ «Средняя линия»

1. Д.п.: построим треугольник LNB: прямые KL и MN пересекаются в точке В

2. Рассмотрим треугольник KMB: LN || KM; LN=KM, т. к. LN=1,8м и KM=3,6м=> LN - средняя линия, => BN=NM=3,6м

3. BC=BN+MN+CM=3,6+3,6+7=14,2 м

4. Треугольник ABC подобен треугольнику LBN по двум углам. Так как в подобных треугольниках стороны, лежащие против равных углов, пропорциональны, то

Ответ: м

3 способ «Тангенс»

Теоретический минимум:

Определение тангенса в прямоугольном треугольнике

Решение:

1) Д.П. найдём точку пересечения прямых АL и СN. Получим точку В. Пусть АС=x м, а NB=y м

2)Находим тангенс угла В в трех прямоугольных треугольниках:

ΔCAB; ΔMKB; ΔNLB:

tg B=tg B=

3) ;2y=3,6+y; y=3,6

4)

Ответ: м

4 способ «Ступеньки»

Теоретический минимум:

Первый признак подобия треугольников (по двум углам).

Пропорциональность отрезков

Решение:

1)Проведем KP||BC; LS||BC;

2)PK=CM=7; SM=LN=1,8; KS=3,6-1,8=1,8; SL=MN=3,6

3) Пусть AP=x м;

4)ΔPAK~ΔSKL, как прямоугольные по острому углу, т.к. ےAKP=ےKLS, как односторонние =>

5)AC=AP+PC=3,5+3,6=7,1

Ответ: м

5 способ «Равенство»

Теоретический минимум:

Признаки равенства прямоугольных треугольников (по катету и острому углу). Первый признак подобия треугольников (по двум углам).

Пропорциональность отрезков

Решение:

1)ΔSKL=ΔNLB (по катету и острому углу), т.к. ےKLS=ےLBN; KS=LN=1,8 м

2) =>NB=3,6 м

3) ΔCAB~ΔN LB, как прямоугольные с общим углом

Ответ:

6 способ «Пропорциональность»

Теоретический минимум:

Первый признак подобия треугольников (по двум углам).

Пропорциональность отрезков

Решение:

1) k=2, =>

MB в 2 раза больше NB и

MB на 3,6 м больше NB, => MB=7,2

2) ΔCAB~ΔMKB (по двум углам).

Ответ: м

Анализ полученных результатов

СРАВНИТЕЛЬНАЯ ТАБЛИЦА

Способ решения задачи

Выступа-ющие

Актуальность, значимость

Наглядность

Полнота раскрытия

Оригинальность

Доходчивость

Эффективность Убедительность

Артистизм, выразительность

Предпочтение

ИТОГ

+

+

+

+

+

+

+

+

1

«Подобие»

Шелухина, Козлова

2

«Средняя линия»

Гвоздева, Тарасова

3

«Тангенс»

Биндюков,

4

«Ступеньки»

Кретова, Константинова

5

«Равенство»

Баскакова, Бабина

6

«Пропорцио-нальность»

Гончарова

7

ИТОГ УРОКА: 1. Для анализа взяли стандартную задачу из КИМов 2015 года. При этом были рассмотрены разные способы ее решения, в том числе и нестандартные подходы. Тем самым произвелось мини-исследование различных способов решения задач. Что дало нам исследование?

А) умение видеть за абстрактными чертежами и сухими числовыми величинами конкретную жизненную ситуацию

5.Обсуждение Д/З: повт п.п.56-61, № 579,580, 581

6.ИТОГ УРОКА

Итак, исследование задачи № 1 дает представление о том, что имеется целый ряд задач практического содержания, решаемых несколькими способами, в том числе и устными. Перейдем к обсуждению представленных способов в решении задачи. Обсуждение состоится после анализа каждой группой каждого метода. Во всех способах присутствовала «Наглядность», «дополнительные построения», что ещё можно добавить?

6. Подведение итогов урока. Рефлексия

Закончить урок хочу словами Мориса Клайна:

«Музыка может возвышать или умиротворять душу,

Поэзия - пробуждать чувства,

Философия - удовлетворять потребности разума,

Интересное дело - совершенствовать материальную сторону жизни людей,

Математика - способна достичь всех этих целей»

Литература: Открытый банк заданий по математике ГИА 2015 www.mathgia.ru</</font>