Тема урока: «Техника дифференцирования»

Тип урока: урок комплексного применения знаний, умений и навыков.

Цель урока:

• организация деятельности учащихся по закреплению и самостоятельному применению знаний, умений, навыков нахождения производных функций;

• развитие логического мышления;

• формирование общих трудовых умений;

Оборудование:

1) карточки-задания тестового контроля (№1);
2) разноуровневые карточки-задания (№2).

Логика урока:

1. Организационный момент

2. Актуализация опорных знаний (карточки №1)

3. Применения комплекса знаний

4. Контроль и самоконтроль (карточки №2 - самостоятельная работа)

5. Домашнее задание

6. Итоги урока

7. Рефлексия

Ход урока

1. Организационный момент

Здравствуйте! Тема нашего урока «Техника дифференцирования». Сегодня на уроке мы будем применять полученные знания по теме «Производная» к решению задач. Решение задач - практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь. Выдающийся математик Д.Пойа говорил:

"Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их", - пусть эти слова станут девизом урока.

Сегодня на уроке мы с вами сначала повторим теоретический материал по теме, т.е. формулы для нахождения производных; затем будем решать задачи с использованием этих формул; в заключении урока проведём небольшую самостоятельную работу, где каждый из вас сможет показать свои знания.

II. Актуализация опорных знаний

Итак, с чего начинаем? Да, повторим теоретический материал:

Возьмите карточку под номером 1. (карточки заранее лежат на партах у каждого учащегося). Один человек с карточкой выходит к доске и на отвороте записывает формулы и ответы. Остальные выбирают правильные ответы из трех предложенных вариантов. В вашем распоряжении 4 минуты. (На другом отвороте доски заранее записаны ответы (б, в, а, б, в, б, а, б)).

Учащиеся сами оценивают своё решение (1 задание - 1 балл) и выставляют на карточке количество набранных баллов.

Итак мы с вами повторили формулы вычисления производных для чего? Для того, чтобы перейти к решению задач

III. Показ образца применения комплекса знаний:

Теперь посмотрим как можно применить ваши знания формул дифференцирования к решению задач. Давайте рассмотрим следующую задачу: (заранее записана с решением на доске). Разбирается задача:

Решите неравенство: , если

Решение:

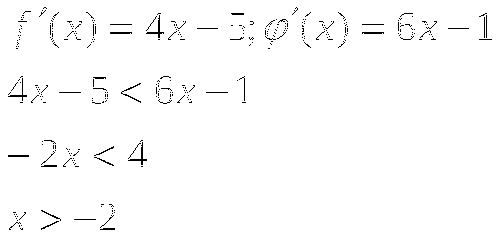
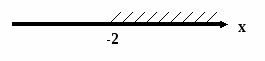
Ответ: х  (-2; +)

А теперь попробуйте решить аналогичную задачу в тетрадях. Под образцом записаны 2 задачи. Кто затрудняется, перепишите решение в тетрадь, а само задание а) решите дома. В вашем распоряжении 5 минут. Ответ заготовлен заранее на плакате. Учащиеся проверяют ответ. Те кто справился с заданием а), задание б) записывают на дом.

а) Решите неравенство: , если

Ответ: х  (- ; 1)

б) Решите неравенство: , если

Ответ: х  (- 4; 3)

Итак, мы с вами применили знания формул дифференцирования к решению более сложных заданий.

IV. Контроль и самоконтроль:

Чем сейчас будем заниматься, что у нас дальше по плану? Правильно настало время проверить и оценить ваши знания. Возьмите карточку №2, на ней задания для самостоятельного решения. Приступайте. Через 20 минут будем проверять ваши работы. Ответы сверим устно. Каждое правильно выполненное задание - 1 балл. (Учащиеся сами подсчитывают количество баллов за работу.)

V. Домашнее задание:

Повторить формулы дифференцирования, решить задания а), б), желающие могут получить дополнительно задания на карточке.

VI. Итоги урока:

Итак, мы сегодня с вами повторяли формулы дифференцирования; вспомним их:

? Производная любого числа равна: нулю

? Производная функции у = х равна: единице

? Производная степенной функции у = хⁿ равна: n х^n-1

? Производная произведения числа на функцию, которая имеет производную, равна: произведению числа на производную функции

? Производная суммы двух функций, каждая из которых имеет производную, равна: сумме производных этих функций

? Производная произведения двух функций u и v, каждая из которых имеет производную, равна: сумме произведений каждой функции на производную другой функции

? Производная частного двух функций u и v, каждая из которых имеет производную, находится по формуле:

? Производная сложной функции вычисляется по формуле:

Подсчитайте, пожалуйста, количество баллов за обе карточки: и оцените свою работу по следующим критериям (открываются на доске).

10 б и более - "5"

8 - 9 б - "4"

6 - 7 б - "3"

Поднимите руки, у кого получилось «5»; «4»; «3». Сдайте тетради на проверку, через 2 урока я их вам верну.

VII. Рефлексия:

В заключение урока я попрошу вас, ответить на вопрос: Получили ли вы удовлетворение от проделанной работы, от урока в целом? И поставить при выходе из кабинета значок на листке, соответствующем вашим ощущениям.

Красный: Настроение улучшилось, прибавилось уверенности в своих знаниях

Зелёный: Никаких изменений в настроении

Синий: Настроение ухудшилось, ощущаю неуверенность в своих знаниях.

Спасибо! До свидания!

Карточка №1 (тестовые задания)

1. Производная числа с равна:

а) с

б) 0

в) 1