- Учителю
- Открытый урок по математике по теме Последовательности 9 класс
Открытый урок по математике по теме Последовательности 9 класс
МБОУ «Ямбухтинская средняя общеобразовательная школа Спасского муниципального района Республики Татарстан»
Муниципальный конкурс методических разработок «Мой лучший урок математики»
Конспект-модель урока
на тему «Последовательности»
по предмету «Математика»
в 9 классе
Учитель: Сафина Гульчачак Гафурбаевна
Стаж работы - общий педагогический - 20лет,
в данной должности - 7 лет
Категория - I
Предмет - Математика
2015 год
Пояснительная записка
Тема урока. " Последовательности"
Место урока в учебном курсе. Урок по теме "Последовательности" подготовлен для обучающихся 9 класса и проводится в разделе "Арифмитические и геометрические прогрессии". На тему "Последовательности " отводится 2 урока. Данный урок является первым уроком по теме.
Тип урока: урок изучения новой темы
Цель урока: познакомить учащихся с понятием последовательности, способами задания последовательности. Выработать умения использовать индексные обозначения и находить n-й член последовательности по заданной формуле.
Задачи урока:
Образовательные: формирование представления о последовательности, знаний о способах задания числовых последовательностей, умений находить члены последовательности по предложенной формуле, а также умений находить саму формулу, задающую последовательность.
Развивающие: развитие умений сравнивать и анализировать, обобщать информацию, делать выводы.
Воспитательные: воспитывать навыки самоконтроля, культуру общения, умение работать в коллективе; воспитывать такие качества характера, как настойчивость в достижении цели, умение не растеряться в проблемной ситуации.
Методологическая база.
Учебник: Алгебра. 9 класс: учеб. для общеобразоват. учреждений / Ю.Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С.А. Теляковского. - 17-е изд. -М.Просвещение, 2008.
Программа: 1) Примерная программа основного общего образования по математике. Сборник нормативных документов. Математика. Составители: Э.Д.Днепров, А.Г.Аркадьев. Москва, «Дрофа», 2009;
2) Программы общеобразовательных учреждений. Алгебра 7-9классы. Составитель: Т.А. Бурмистрова. Москва, «Просвещение», 2009;
Использовались интерактивные методы обучения - игровой, проблемный.
Отличительные особенности урока относительно традиционного.
Тему, цели и задачи данного урока формулируют сами учащиеся. Учащиеся осуществляют учебные действия по намеченному плану (применяется групповой, индивидуальный метод) Для лучшего усвоения темы подготовлена презентация. Наглядное сопровождение сделает новый материал более доступным, легко запоминающимся и интересным. Материал урока связан с жизнью. На уроке создается ситуация для формирования самостоятельного мышления, активной учебной деятельности, познавательных интересов учащихся средствами самого материала урока. На уроке используются элементы самоконтроля и самооценки учащихся, оценки своих возможностей. Межпредметные связи: история, английский язык, биология.
Оборудование: Презентация, карточки, "Контрольно-измерительные материалы по математике ОГЭ» ФИПИ И.В.Ященко 2015 г. , фильм о Числах Фибоначчи, карточки, оценочный лист.
Ход урока:
-
Организационный момент.
- Добрый день, ребята! Каково ваше настроение? Давайте поприветствуем одноклассников улыбкой и сохраним хорошее настроение в течение всего урока. (Слайд 1)
-
Актуализация знаний.
Устная работа. (Слайд 2)
-
Найдите значение выражения
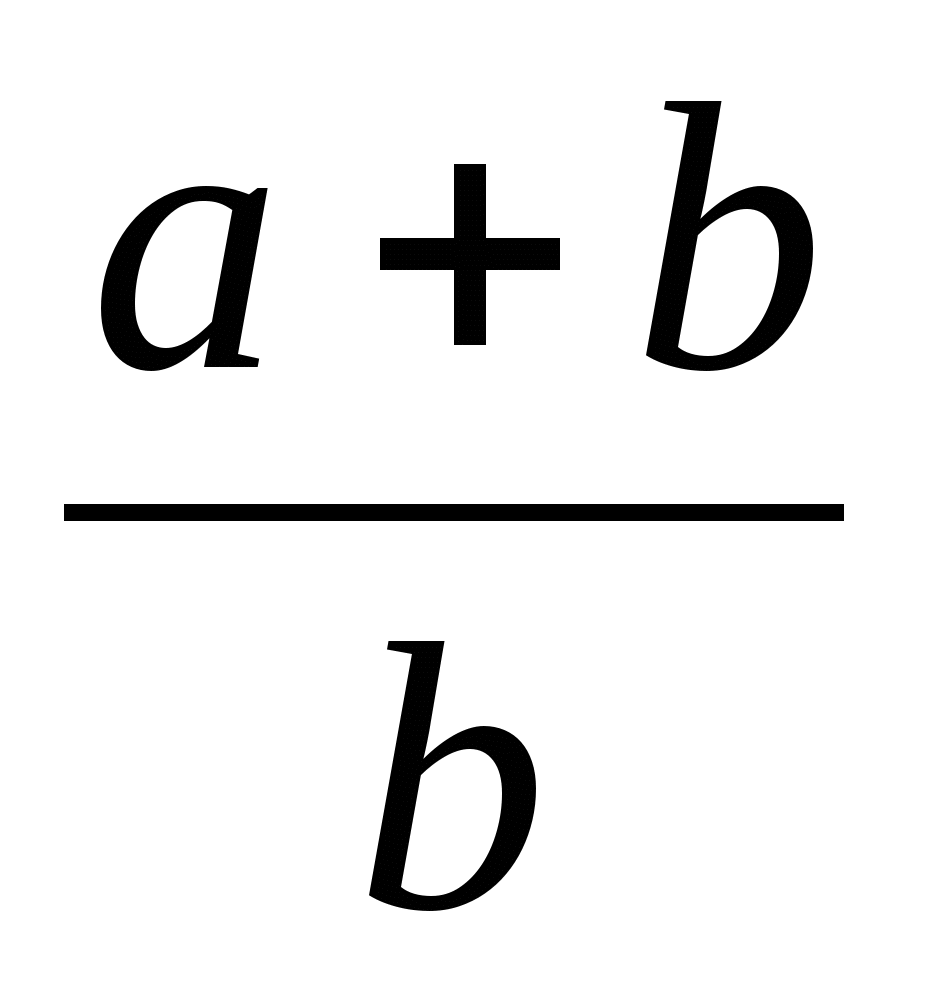 при а= - 2,5 и b=3.
при а= - 2,5 и b=3.
-
Найдите значение выражения
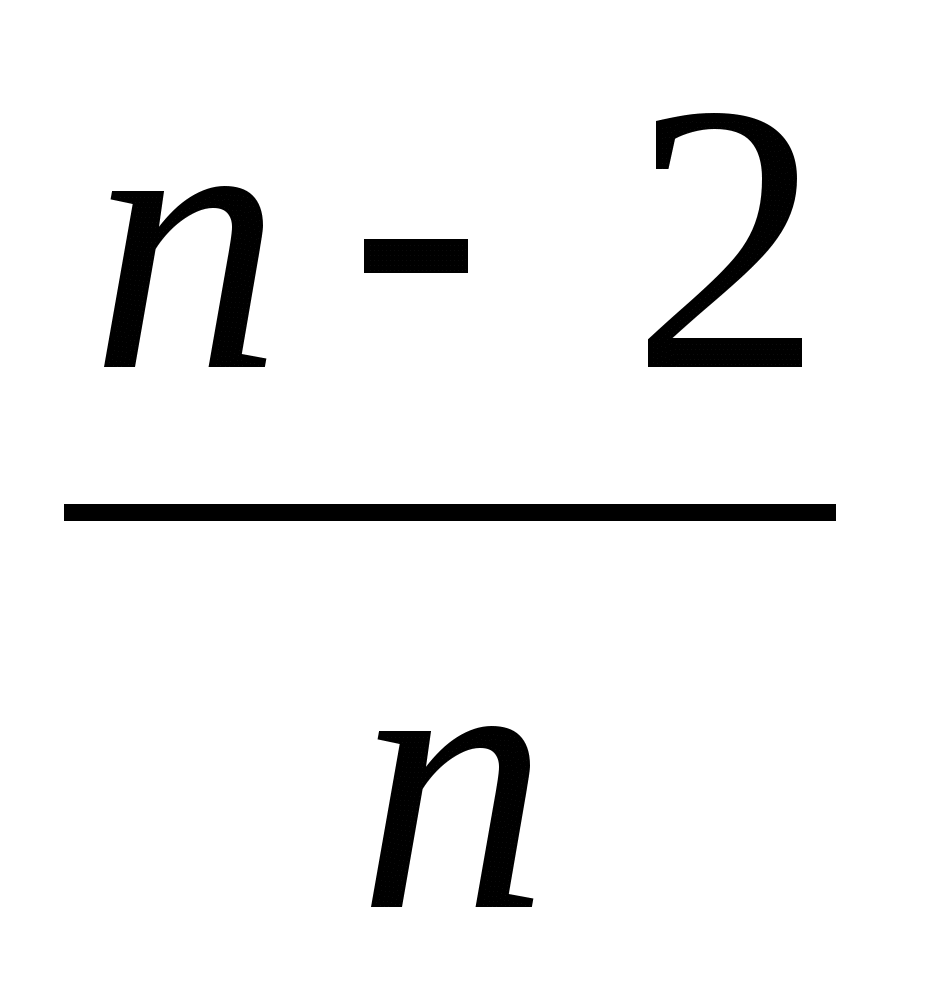 при =1; 3;10. При каких n имеет смысл это выражение?
при =1; 3;10. При каких n имеет смысл это выражение?
-
Напишите формулу четных чисел; кратных 5; кратных 2 и 5.
-
Подготовка к восприятию новых знаний.
- А теперь представим, что мы профессора математической лаборатории и
занимаемся изучением математических математических закономерностей. (Слайд3)
- Значит мы какие ? (- Умные, серьезные, про математику знаем всё и т.д.)
-Вот перед нами лежат математические "вещества", и нам предстоит их
исследовать и все результаты внести в рабочие листы.
-
Изучение нового материала.
- Выполним задание и определим какие математические "вещества" написаны на карточках. (Приложение 1)
Найдите закономерности:
1,4,7,10,13...
2,6,18,54, 162...
10,19,37,73,145...
1,2,3,4,5,6,7,8.9.
![]() ,
,
![]() ,
,![]() ,
,![]() ...
...
5;5;5;5;5...
33, 31, 32, ...
- Да, это числовые ряды. Как стоят эти числа в рядах? (последовательно) Значит, они называются последовательностями. И так, тема нашего урока? (Последовательности) Запишем тему в рабочих листах. Какую цель вы поставите себе на данном уроке? (Изучение числовых последовательностей) (Слайд 5)
- В жизни какие события происходят последовательно? (Дни недели, названия месяцев, нумерация домов, и т.д.) (Слайд 13-19)
- Посмотрим последовательность четных чисел (2,4,6,8,...) . Числа образующие последовательность , называются членами последовательности и нумеруются.
а1; а₂; а₃; а₄;…аn; ... («а первое», «а второе», «а n-ое», …) (Слайд 6)
Последовательность а₁; а₂; а₃; а₄;…аn; ... обозначают обычно (аn)
- В последовательности 1;4; 7;10;13;… укажите а₁; а₃; а5.
- Переходим к следующему этапу исследования нужно изучить свойства последовательностей.
КЛОК БАДДИС. - Сравните последовательности и на какие группы можно их разделить? Расскажите об этом партнеру, с которым вы назначали встречу в 3 часа. Начинает тот, кто выше. (Учащиеся обсуждают вопрос, используя ТАЙМД-ПЭА-ШЭА, затем несколько учащихся проговаривают то, что услышали от своего партнера)
-Сделаем вывод. (Последовательности бывают конечные и бесконечные, возрастающие и убывающие)
- Зачем мы изучаем последовательности? (Для того чтобы узнать любой член последовательности.)
- Какими способами можно задать последовательности? (Словами, формулой)
- Последовательности можно задать различными способами. (Слайд 7)
А) Описательный
Например, на четных местах 0, на нечетных - единица.
Б) Формулой n - ого члена последовательности
аn =2 n, n - натуральное число. При n=1, а₁=2·1=2, при n=2, а₁=2·2=4, и т.д.
В) Название следующего способа задания последовательности - рекурретный - произошло от слова «recurro» - возвращаться. Рекуррентной называется формула, выражающая любой член последовательности, начиная с некоторого, через предыдущие.
Для некоторых последовательностей рассмотренных в начале урока, запишем рекуррентные формулы:
1,4,7,10,13... а₁=1, аn+1= аn+3
2,6,18,54, 162... а₁=2, аn+1= аn ·3
10,19,37,73,145... а₁=10, аn+1= аn ·2 - 1
Физкультминутка
-
Закрепление нового материала.
-Давайте, теперь определим как наши открытия помогут выполнить задания №560, №564, №565 (а) №569 (а), 567. В оценочных листах оцените себя, если есть затруднения, то пишите вопросы. (После каждого задания ответы проверяются по слайдам 8-12)
1) №560
Выпишите первые несколько членов последовательности натуральных чисел, кратных 3, взятых в порядке возрастания. Укажите ее первый, пятый, десятый, сотый и n-й члены.
Решение: 3; 6; 9; 12; … а1 = 3, а5 = 15, а10 = 30, а100 = 300, аn = 3n
2) №564
Перечислите члены последовательности (хn), которые расположены между: а) х31 и х35, г ) хn-2 и xn+2.
Решение: а) х32, х33, х34; б) xn-1, xn, xn+1.
3) №565 (а)
Найдите первые шесть членов последовательности, заданной формулой n- го члена: хn = 2n - 1.
Решение: х1 = 1, х2 = 3, х3 = 5, х4 = 7, х5 = 9, х6 = 11.
4) №569 (а)
Выпишите первые пять членов последовательности (аn), если а1 = 1, аn+1 = аn +1.
Решение: 1, 2, 3, 4, 5.
№567 (для сильных учащихся)
Последовательность аn задана формулой аn=n2-n-20. Определите номера отрицательных членов и вычислите их.
Решение: а1=-20, а2=-18, а3=-18, а4=-8
Самостоятельная работа
(Контрольно-измерительные материалы по математике ОГЭ ФИПИ И.В.Ященко 2015 г. Вариант 32,33 №6 )
а) Последовательность задана формулой сn=3n2 - 2. Какое из чисел является членом этой последовательности?
-
45 2)46 3) 47 4)44
б) Последовательность задана формулой
cn=2n+ 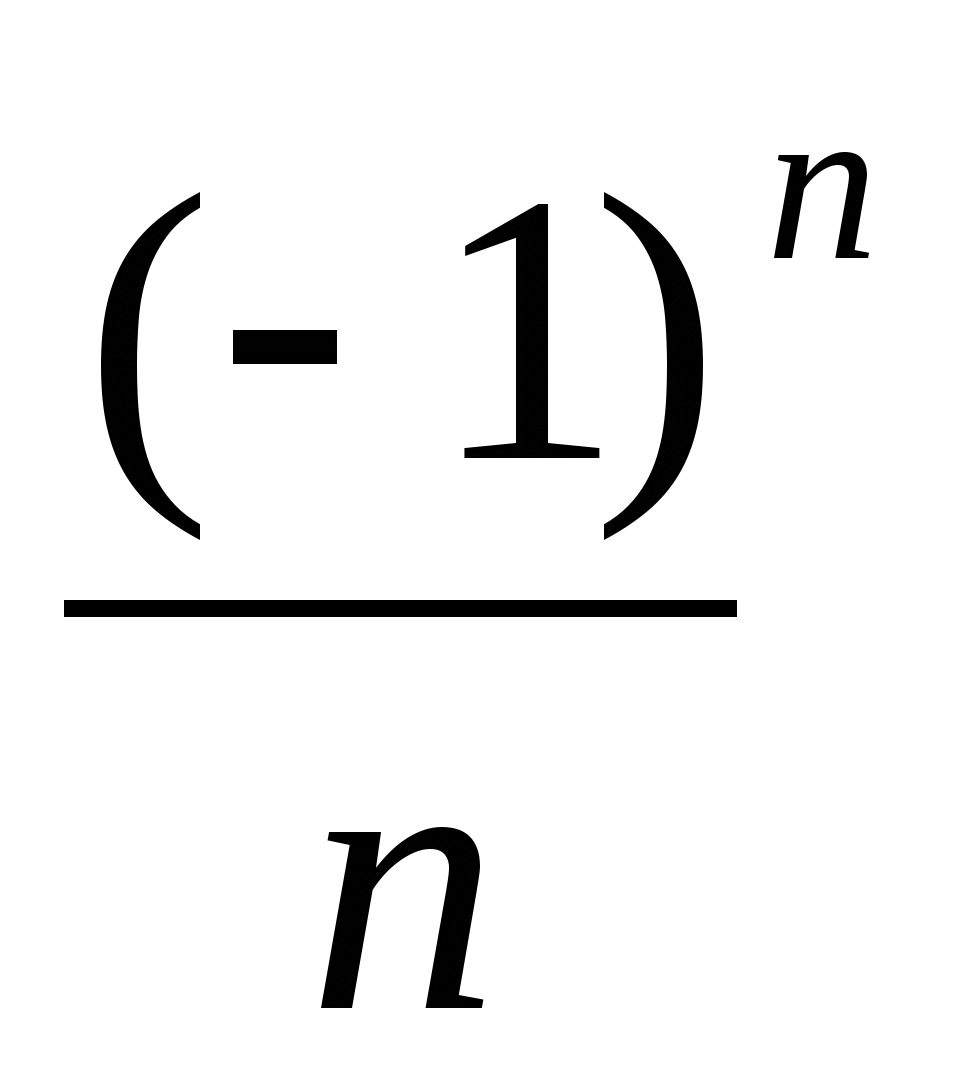
![]()
![]()
![]()
![]()
- Сегодня мы познакомимся со знаменитой последовательностью:
1, 1, 2, 3, 5, 8, 13, 21, …, (Слайд 20) Каждое число, начиная с третьего, равно сумме двух предшествующих. Этому ряду натуральных чисел, имеющему своё историческое название - ряд Фибоначчи, присуща своя логика и красота. Леонардо Фибоначчи (1180-1240). Крупный итальянский математик, автор «Книги абака». Эта книга несколько веков оставалась основным хранилищем сведений по арифметике и алгебре. Именно по трудам Л. Фибоначчи вся Европа осваивала арабские цифры, систему счета, а также практическую геометрию. Они оставались настольными учебниками, чуть ли не до эпохи Декарта (а это уже 17 век!).
Посмотрите фильм о том, как встречаются числа Фибоначчи в явлениях природы.
VI. Рефлексия
- Что узнали нового? (последовательности)
- Как можно задать числовые последовательности? (словесно, формулой n- го члена, рекуррентным способом)
- Какие бывают последовательности? (конечные, бесконечные, возрастающие, убывающие)
- Где может пригодиться умение работать с последовательностями? (при дальнейшем изучении математики, при сдаче ОГЭ и в жизни)
- Какие трудности у вас возникли при решении задач?
- Проанализируйте свою работу на уроке.
Домашнее задание: п. 24, № 562, 565 (в, д), 573(а). Для желающих
Решите задачу: В январе вам подарили пару новорожденных кроликов. Через два месяца у них рождается новая пара кроликов, в следующем месяце - еще одна пара и т.д. ежемесячно. С каждой новой парой кроликов происходит то же самое. Сколько пар кроликов будет у вас в декабре, если ни одна пара не погибнет?
Литература
-
Алгебра. 9 класс: учеб. Для общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К. И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. - 17-е изд.-М,2008.
-
Д.Ф.Айвазян Поурочные планы по алгебре 9 класса по учебнику Макарычева Ю.Н. и др. «Корифей» Волгоград 2008г.
-
Дидактические материалы по алгебре Ю.Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева, М: Просвещение, 2009.
-
Журнал «Мәгариф» №3 2014г, №6 2015г.
Приложение 1

Приложение 2
Оценочный лист
ФИО ____________________________________________
Задания
Балл
Вопросы
№560
№564
№565 (а)
№569 (а)
№567
Самостоятельная работа
5 б. - все понял и могу объяснить другому;
4 б. - сам понял, но объяснить не берусь;
3 б. - для полного понимания надо повторить;
2 б. - я ничего не понял.