- Учителю
- Методика изучения математических понятий на примере «возрастающей и убывающей функции» в 7-9 классах (А. Г. Мордкович, Алгебра - 7 (8, 9) . Учебник)
Методика изучения математических понятий на примере «возрастающей и убывающей функции» в 7-9 классах (А. Г. Мордкович, Алгебра - 7 (8, 9) . Учебник)
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
КОРНИЛОВА Е.А.
УЧИТЕЛЬ МАТЕМАТИКИ МАОУ СОШ №10 Г.ТАГАНРОГА
МЕТОДИКА ИЗУЧЕНИЯ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ НА ПРИМЕРЕ «ВОЗРАСТАЮЩЕЙ И УБЫВАЮЩЕЙ ФУНКЦИИ» В 7-9 КЛАССАХ
(А. Г. МОРДКОВИЧ. АЛГЕБРА - 7 (8, 9). УЧЕБНИК.)
Понятия «возрастающая и «убывающая функция» являются одними из основных и важных в школьном курсе математики. Знакомство с ними начинается в 7 классе, при их изучении у учащихся возникает масса различных трудностей, и в связи с этим учителю достаточно трудно на первых уроках работать с этими понятиями.
Разработанный ряд методико-математических заданий дает возможность учителю сформировать понятия «возрастающая и убывающая функция» на простейших (житейских) примерах, позволяющих представить картины реального мира, связанные с рассматриваемым понятием и существенно облегчить его понимание. Задания приводятся в вопрос-ответной форме; предполагается, что задания, промежуточные выводы и вопросы принадлежат учителю, а ответы - ученику.
Вопрос, задание. Даны графики функции у=кх+m (рис. 1). Разделите их на две группы и объясните, какими признаками Вы руководствовались при выполнении задания.
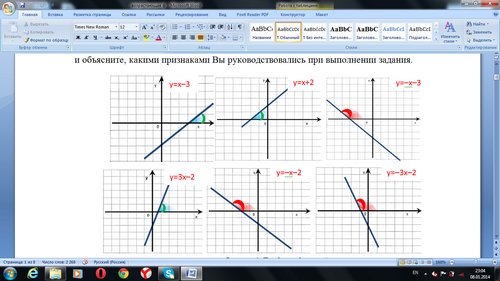
Рисунок 1. Графики функций.
Ответ.1 группа: у=х-3; у=х+2; у=3х-2,2 группа: у= -х-3; у= -х+2; у= -3х-2.
При выполнении задания руководствовались следующими признаками:
- Коэффициент к>0 (k<0)
- График с положительным направлением оси ОХ образует острый (тупой) угол.
Рассмотрим первую группу. Графиками данных функций является прямая, которая образует острый угол с положительным направлением оси ОХ, и у этих функций к>0. Кроме того, у этих функций есть еще общие особенности, с которыми нам поможет познакомиться вот этот человечек![]() .
.
Все что он умеет делать, так это только двигаться справа налево или слева направо. Наша задача: определиться с направлением его движения, чтобы это не противоречило выбранному направлению оси Ох.
Вопрос. Кто может сказать, как и почему так человечек будет двигаться?
Ответ. Слева направо, так как направление движения оси Ох указано стрелочкой.
Давайте посмотрим (рис. 2), что происходит с абсциссами и ординатами точек графиков функций при движении человечка по графику слева направо.
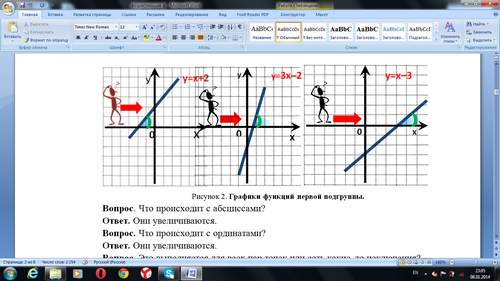
Рисунок 2. Графики функций первой подгруппы.
Вопрос. Что происходит с абсциссами?
Ответ. Они увеличиваются.
Вопрос. Что происходит с ординатами?
Ответ. Они увеличиваются.
Вопрос. Это выполняется для всех пар точек или есть какие-то исключения?
Ответ. Это выполняется для всех пар точек.
Тогда можно сделать вывод о том, что если человечек будет двигаться по этим графикам слева направо, то ординаты точек графиков все время будут увеличиваться, он будет как бы «подниматься в горку».
В таких случаях математики употребляют термин возрастание функции и говорят так: если k>0, то линейная функция y=kx+m на всей области определениявозрастает.
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции, которые возрастают. Приведем примеры из жизни.
Еще из детской сказки «Три медведя» мы знаем, что с увеличением роста медведя, ему нужна большая кровать, большему медведю соответствует большая тарелка и ложка, меньшему медведю - меньшая кровать, меньшая тарелка и ложка (рис. 3).
Задание. Предложить детям привести из повседневной жизни еще примеры возрастания функции. Если возникнут затруднения, то можно рассмотреть примеры учителя.
Например, чем больше слов в телеграмме, тем она дороже; чем больше растений в помещении, тем больше там кислорода.
Чтобы убедиться, что это возрастающие функции, изобразим графиком, как возрастает, например, стоимость телеграммы по мере увеличения количества слов. Тариф задан математической моделью y=3x-2, где х - количество слов, у - стоимость телеграммы (рис.4).
Рисунок 3. Три медведя.
Вопрос. Из практики мы знаем, что эта функция возрастает. Докажите это пользуясь полученным графиком и имеющимися знаниями о возрастающей функции.
Ответ. Если мы будем двигаться по графику этой функции слева направо, то мы будем «подниматься в горку», а значит, функция возрастает.
Вопрос. Но у нас получается, что функция может принимать отрицательные значения, то есть стоимость телеграммы будет отрицательной. Может ли такое быть?
Ответ. Нет, стоимость всегда положительна.
Вопрос. Тогда нужно было изначально в математической модели ввести ограничения на переменную х. Какие это должны быть ограничения?
Рисунок 4. График функции у=3х-2.
Ответ. Так как переменная х - это количество слов, то она не должна принимать отрицательные значения и должна быть целым числом, то есть х - натуральное число.
Вопрос. Тогда как будет выглядеть уточненная модель этой ситуации?
Ответ. Уточненная модель этой ситуации выглядит так: у=3х-2, где х - натуральное число, то есть х принадлежит множеству натуральных чисел.
В математике условились вместо фразы «х принадлежит множеству Х» писать 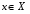 (читают: «элемент х принадлежит множеству Х, знак
(читают: «элемент х принадлежит множеству Х, знак 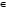 - знак принадлежности).
- знак принадлежности).
Если линейную функцию у=кх+m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового промежутка Х, то пишут: у=кх+m, 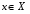 .
.
Аналогичные рассуждения можно провести и для другой группы графиков функций.Рассмотрим вторую группу графиков функций у= -х-3; у= -х+2; у= -3х-2.
Вопрос. Опишите общие свойства данных графиков.
Ответ. Графиками данных функций является прямая, которая образует тупой угол с положительным направлением оси ОХ, и у этих функций к<0.
Давайте посмотрим (рис.5), что происходит с абсциссами и ординатами точек графиков функций при движении человечка по графику слева направо.
Рисунок 5. Графики функций второй подгруппы.
Вопрос. Что происходит с абсциссами?
Ответ. Они увеличиваются.
Вопрос. Что происходит с ординатами?
Ответ. Они увеличиваются.
Вопрос. Это выполняется для всех пар точек или есть какие-то исключения?
Ответ. Это выполняется для всех пар точек.
Вопрос. Что происходит с ординатами точек при движении человечка слева направо и как это можно сравнить с движением по горке?
Ответ. Если человечек будет двигаться по этим графикам слева направо, то ординаты точек графиков все время будут уменьшаться, он будет как бы «спускаться с горки».
В таких случаях математики употребляют термин убывание функции и говорят так: если k<0, то линейная функция y=kx+m на всей области определения убывает.
Пример проявления свойства убывания функции предложить детям придумать самостоятельно. Если ответов не последует, можно подсказать: чем дальше от начальника, тем меньше работы; чем больше знаменатель, тем меньше дробь и т.д.
Наглядно убывание функции можно проследить на рис. 6.

Рисунок 6. Наглядное представление убывающей функции.
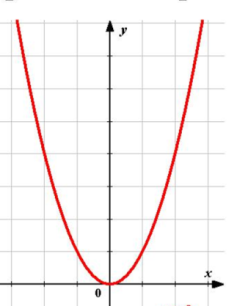
Рассмотрим графики функций у=кх2 , при к<0 и к>0.
Описывать свойства возрастания и убывания этой функции мы будем, опираясь на ее геометрическую модель - параболу (рис. 7).
При к>0
у=х2
При к<0
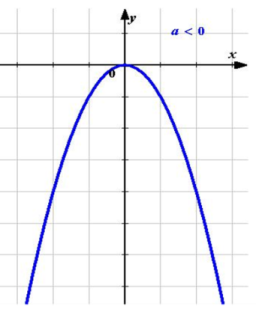
у= -х2
Рисунок 7. Парабола.
Вопрос. Попробуйте, глядя на рисунки, описать свойства возрастания или убывания функции, пользуясь понятиями «подниматься в горку», «спускаться с горки».
Ответ. На луче (-∞;0] функция у=х2 убывает, при этих значениях х, двигаясь по параболе слева направо, мы «спускаемся с горки», на луче [0;+∞) функция у=х2 возрастает, при этих значениях х, двигаясь по параболе слева направо, мы «поднимаемся в горку».
На луче (-∞;0] функция у= -х2 возрастает, при этих значениях х, двигаясь по параболе слева направо, мы «поднимаемся в горку», на луче [0;+∞) функция у= -х2 убывает, при этих значениях х, двигаясь по параболе слева направо, мы «спускаемся с горки».
Таким образом, график функции у=кх2 является примером разбиения области определения на два промежутка, на одном из которых функция возрастает, а на другом убывает.
Возникает вопрос, а может ли быть такое, что область определения разбивается на два промежутка, на каждом из которых функция только возрастает или только убывает?
Оказывается, что может.
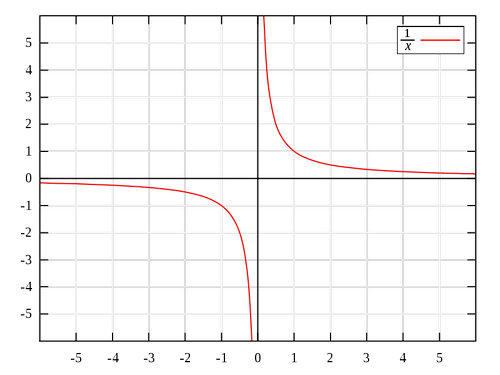
Убедиться в этом нам поможет график функции у=к/х, при к<0 и к>0.
Описывать свойства возрастания и убывания этой функции мы будем, опираясь на ее геометрическую модель - гиперболу (рис. 8).
При к>0
При к<0
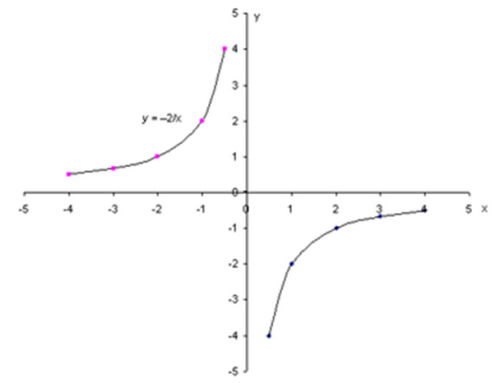
Рисунок 8. Гипербола.
Вопрос. Опишите свойства возрастания или убывания функции, пользуясь понятиями «подниматься в горку», «спускаться с горки».
Ответ. На луче (-∞;0] функция у=1/х убывает, при этих значениях х, двигаясь по гиперболе слева направо, мы «спускаемся с горки», на луче [0;+∞) функция у=1/х убывает, при этих значениях х, двигаясь по гиперболе слева направо, мы «спускаемся с горки».
На луче (-∞;0] функция у= -2/х возрастает, при этих значениях х, двигаясь по параболе слева направо, мы «поднимаемся в горку», на луче [0;+∞) функция у= -2/х возрастает, при этих значениях х, двигаясь по параболе слева направо, мы «поднимаемся в горку».
Итак, график функции у=к/х является примером разбиения области определения на два промежутка (открытых луча) на каждом из которых функция возрастает (убывает).
Вопрос. С какими особенностями графиков возрастающих (убывающих) функций относительно разбиения области определения мы познакомились?
Ответ. Мы познакомились с графиками функций, которые:
-
возрастают или убывают на всей области определения,
-
когда область определения делится на два промежутка, в одном из которых функция возрастает, а в другом убывает,
-
когда область определения делится на два промежутка, на каждом из которых функция возрастает (убывает).
Возникают вопросы, существуют ли функции, у которых область определения разбивается на разное количество промежутков, и на всех этих промежутках функция ведет себя по-разному, может ли функция ни возрастать и ни убывать на всей области определения. Ответить на них поможет график кусочной функции 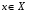 (рис. 9).
(рис. 9).
Вопрос. На какие промежутки разбит график функции?
Ответ. (-∞;-2), [-2;0), [0;2), [2;+∞)
Вопрос. Как ведет себя функция на этих промежутках, она возрастает или убывает?
Ответ. На (-∞;-2) функция не возрастает и не убывает, она постоянна,
на [-2;0) функция убывает,
на [0;2) функция возрастает,
на [2;+∞) функция не возрастает и не убывает, она постоянна,
Вопрос. До сих пор при выявлении свойств возрастания или убывания функции мы пользовались только признаками «подниматься в горку» и «спускаться с горки». Однако математики не очень жалуют способ исследования свойств функции с помощью рассуждений «движение в горку», «движение с горки». Они считают, что определения понятий не должны опираться на рисунок, - чертеж должен лишь иллюстрировать то или иное свойство функции на ее графике. Попробуйте дать строгие определения понятий возрастания и убывания функции.
Рисунок 9. График кусочной функции.
Определение. Функцию y=f(x) называют возрастающей на промежутке Х, если из неравенства х1<x2, где х1 и x2 - любые две точки промежутка Х, следует неравенство f(x1)<f(x2) (рис.10).
Определение. Функцию y=f(x) называют убывающей на промежутке Х, если из неравенства х1<x2, где х1 и x2 - любые две точки промежутка Х, следует неравенство f(x1)>f(x2) (рис.11).
На практике удобнее пользоваться следующими формулировками.
Функция возрастает, если большему значению аргумента соответствует большее значение функции.
Например, большему дереву соответствует большая крона (рис. 12).
Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Например, большей глубине соответствует меньшая освещенность (рис. 13).
Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
У2
Х1
Х2
у
х
У111
Рисунок 10.График функции, возрастающей на промежутке Х.
Отметим еще одно обстоятельство: если функция возрастает в своей естественной области определения, то обычно говорят, что функция возрастающая (убывающая) - без указания числового промежутка Х.
У
У1
У1
Х2
Х1
Х
Рисунок 11.График функции, убывающейнапромежутке Х.
Рисунок 12. Дерево и его крона.
Согласно введенным определениям составим алгоритм, по которому мы сможем выяснить характер монотонности функции.
Алгоритм определения монотонности функции на промежутке Х.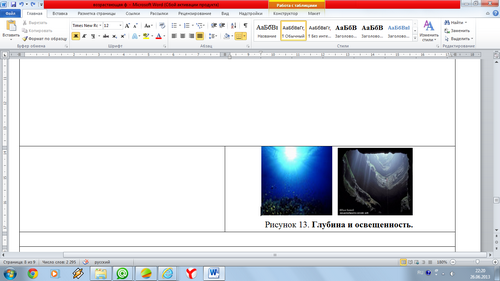
-
Выбрать любые две точки х1 и х2 из промежутка Х.
-
Сравнить х1и х2.
-
Вычислить значение f(x1) и f(x2).
-
Составить разность f(x1) - f(x2).
-
Сравнить разность (f(x1) - f(x2)) с нулем.
-
Если х1< х2 и
разность (f(x1)-f(x2))>0 , то функция возрастает на промежутке Х,
если разность (f(x1)-f(x2))<0, то функция убывает на промежутке Х,
если разность (f(x1)-f(x2))=0, то функция ни убывает и ни возрастает на промежутке Х.
Формирование практических умений
-
Функция
 - возрастающая на области определения.
- возрастающая на области определения.
Доказать это.
Доказательство.
Выражение 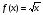 имеет смысл лишь при х> 0. Поэтому D(f) = [0; +∞), значит мы будем рассматривать заданную функцию на промежутке Х=[0; +∞).
имеет смысл лишь при х> 0. Поэтому D(f) = [0; +∞), значит мы будем рассматривать заданную функцию на промежутке Х=[0; +∞).
-
Выберем произвольные х1 и х2 принадлежащие промежутку Х.
-
Пусть х2>х1> 0.
-
При х1 функция примет значение
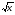 f (х1)=
f (х1)= , прих2 функция примет значение
, прих2 функция примет значение 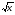 f (х2)=
f (х2)=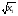 .
. -
Рассмотрим разность f(х2)-f(х1) и преобразуем ее:
 .Числитель и
.Числитель и
знаменатель дроби 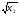 - положительные числа. Это следует из того, что
- положительные числа. Это следует из того, что 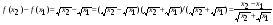 .
.
5. Значит, при х2>х1 выполняется f(х2) - f(х1)> 0, а это значит, что выполняются все условия в определении возрастающей функции и по определению функция  - возрастающая на области определения. Ч.т.д.
- возрастающая на области определения. Ч.т.д.
-
Функция
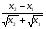 - убывающая на области определения.
- убывающая на области определения.
Доказать это.
Доказательство.
Выражение имеет смысл при любом значении х.
Поэтому D(f)=(-∞; +∞), значит, мы будем рассматривать заданную функцию на промежутке Х=(-∞; +∞).
1. Выберем произвольные х1 и х2 принадлежащие промежутку Х.
2. Пусть х2> х1> 0.
3. При х1 функция примет значение f (х1)=5-2х1 , при х2 функция примет значение f (х2)= 5-2х2
4. Рассмотрим разность (f(х2) - f(х1)) и преобразуем ее:
f(х2) - f(х1)= 5-2х2-5+2х1=2(х1 - х2).
Разность (х1 - х2) - отрицательное число. Это следует из того, что х2>х1>0.
5. Значит, при х2>х1 выполняется f(х2) - f(х1)<0, а это значит, что выполняются все условия в определении убывающей функции и по определению функция 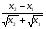 убывающая на области определения. Ч.т.д.
убывающая на области определения. Ч.т.д.
-
Сравнить
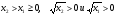 и
и 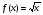 .
.
Решение.
Введем функцию у=2х. Она возрастает, значит для любых двух чисел х1 и х2 таких, что х1<x2 выполняется f(x1)<f(x2). Тогда, возвращаясь к условию задачи, так как 2010<2011, то и 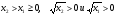 <
<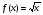 по определению возрастающей функции.
по определению возрастающей функции.
Ответ. 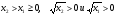 <
<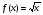
4. Решить уравнение 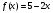
Легко видеть, что х =1 - корень уравнения. Покажем, что других корней это уравнение не имеет. Действительно, область определения функции 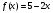 множество положительных чисел. На этом множестве функция возрастает, так как каждая из функций
множество положительных чисел. На этом множестве функция возрастает, так как каждая из функций 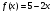 ,
, 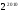 ,
, 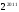 на промежутке(0; +∞) возрастает. Следовательно, данное уравнение других корней, кроме х=1, не имеет.
на промежутке(0; +∞) возрастает. Следовательно, данное уравнение других корней, кроме х=1, не имеет.
Ответ. 1.
Положительные стороны использования предложенного набора методико-математических заданий:
-
существенное снижение вероятности непринятия учащимися учебного материала;
-
обеспечение качественной подачи материала, подлежащего прочному запоминанию;
-
отработка умений и навыков при работе с математическим понятием;
-
развитие математической грамотности и т.д.
Его методическая ценность в том, что ученику нужно глубже вникать в существо задания, выделять главные моменты, учитывая связи между компонентами и т. д. Благодаря этому учебные знания, умения и навыки, на формирование которых направлено это задание, вырабатываются быстрее, так как они связаны с продуктивной мыслительной деятельностью обучаемого.
Еще одно достоинство представленных методико-математических заданий заключается в том, они способствуют формированию гибкости ума, освобождению мышления от шаблонов.С помощью такого средства организации изучения создаются задания, которые могут служить мостиком от стандартных задач к нестандартным.
Рассматривать методико-математические задания только с учетом связи с учебным материалом и без учета воздействия их на мыслительную деятельность ученика нецелесообразно. Поэтому в основу таких заданий положены два существенных свойства понятия «методико-математические задания»: связь с учебным материалом и воздействие на мыслительную деятельность учащихся.