- Учителю
- Сборник задач по математике военно-прикладного характера
Сборник задач по математике военно-прикладного характера
Омский кадетский военный корпус МО РФ
Математические задачи как
средство
военно-патриотического
воспитания кадет
Преподаватель математики
Леонова Валентина Федоровна
.

2016
На фоне современных требований к дифференциации и специализации образования, повышения его качества изучение математики составляет неотъемлемую часть полноценного образования, под которым подразумевается не только получение определённой суммы знаний в некоторой области, но и всестороннее развитие творческой личности.
Не секрет, что математика для учащихся входит в категорию "трудных" предметов. Это происходит потому, что учащиеся не видят практическую сторону математики. А математика и наша жизнь очень тесно связаны между собой. Все, что окружает нас в жизни, в той или иной степени связано с понятием или с законом из математики. Современное производство, с его высоким уровнем механизации, широкой автоматизацией контроля и управления технологическими процессами, применением электронно-вычислительной техники, все более и более требует от современного человека инженерно-технических знаний, понимания научных принципов производства, высокого уровня развития мышления, творческих способностей. Начинать развивать эти качества нужно в период обучения в школе, когда формируется личность с ее взглядами, убеждениями, знаниями, умениями и способностями.
Значительный потенциал для развития творческого мышления учащихся и формирования эмоционально ценностного отношения к окружающему миру несут в себе задачи прикладного характера. При решении таких задач возрастает глубина понимания учебного материала, познавательная активность и творческая самостоятельность, приобретаются навыки, необходимые для жизни в обществе.
Математика всегда была неразрывно связана со сферами человеческой деятельности, в т. ч. и военного дела. Её роль особенно возросла в эпоху научно-технического прогресса и связанной с ним революции в военном деле. Развитие ЭВМ существенно расширило сферу применения математических методов исследования, повысило их эффективность.
Математические методы используются при разработке способов боевого применения новых систем оружия, которые не могут быть подвергнуты натурным испытаниям в мирное время, а также при разработке способов борьбы с новым оружием, которое имеется или может появиться у противника.
В современной военной теории и практике применяются практически все разделы математики: теория вероятностей, математическая статистика, теория игр, теории сетевого планирования и управления, методы экспертных оценок, математическое программирование и др.
Математика играет важную роль при исследовании законов и закономерностей вооруженной борьбы. Опыт позволяет выделить следующие основные задачи, в решении которых успешно применяются математические теории и методы: управление силами и оружием; оптимизация программ в военном строительстве; прогнозирование хода боя операции; разработка вариантов боевых действий войск; оптимизация выбора систем оружия и военной техники. Математика широко используется при решении оперативно- тактических, военно-технических, военно-экономических и других задач.
История и современное состояние применения математики в военном деле показывают, что связь военной науки и практической деятельности вооруженных сил с математикой есть непрерывно развивающийся во времени объективный процесс. Количество военных задач, решаемых с помощью математических методов и средств автоматизации, особенно в области прогнозирования развития военной науки, военной техники и оружия, а также при выработке решений, непрерывно растёт.
Очевидно, что объективной необходимостью во все времена при образовании офицера армии и флота была математическая наука. Чтобы умело руководить войсками, командные кадры должны иметь крепкие знания по математике; математика становится в руках командира важнейшим оружием при решении поставленных задач.
В системе кадетского образования на уроках математики преподаватели рассказывают будущим защитникам Отечества о применении математики на военной службе, о том, что глубокие знания точных наук необходимы для овладения основами военной техники, военного искусства, многими профессиями, нужными в армии.
Решая прикладные задачи, кадеты более глубоко усваивают теоретические вопросы, у них появляется представление о взаимосвязи математики с различными науками. Решение прикладных задач способствует развитию логического мышления, умения кратко, ясно и последовательно выражать свои мысли, принимать оптимальные решения в сложной ситуации.
Предлагая задачи на военную тематику, преподаватель прививает кадетам такие личностные качества, как пытливость, настойчивость, находчивость, развивают самостоятельность, способствуют воинскому воспитанию обучаемых, воспитанию чувства гордости за свою Родину, за труд ученых, инженеров и рабочих, создавших боевую технику.
Необходимым условием успешной учебной деятельности кадетов является интерес к изучаемому предмету, потребность понимания. На основе интереса происходит мобилизация внимания, стремлений, чувствительного и мыслительного восприятия. Военно-прикладная направленность курса математики решает проблему воспитания интереса у кадетов к изучаемому материалу, формирует профессиональные знания. Для воспитания и развития интереса к предмету преподаватель располагает в основном двумя возможностями: работой на уроке и внеклассной работой. Главной из них является, конечно же, работа на уроке, где присутствуют все кадеты.
Одной из форм работы, которая помогает систематически воспитывать интерес кадетов к математике, является решение военно-прикладных задач. Мотивация и интерес кадетов к творческому решению практических задач, а также способность выполнять эту работу гораздо важнее и эффективнее простого накопления знаний. Кадетам можно предложить ряд специально подобранных военно-прикладных задач, а также предлагается самим подобрать или составить прикладные задачи по изучаемой теме. Задачи должны быть актуальны с точки зрения обучаемых, захватывать их и побуждать к решению. Решение задач должно способствовать развитию воображения и проявлению творческих способностей.
Каковы же действия кадетов? Они могут получить консультацию у преподавателя, обратиться за помощью к командирам и воспитателям, воспользоваться учебной и научной литературой, вычислительной техникой. При таком подходе к обучению достигается максимально осознанная кадетами необходимость приобретения конкретных знаний. Решение задач обсуждается в ходе изучения темы и на итоговом занятии по изучаемой теме. Каждому кадету дается возможность защитить свое решение, а также оценить своего товарища. Обучение через решение прикладных задач обеспечивает индивидуализацию и активизацию учебного процесса, а поэтому и более высокую эффективность его.
Выданные кадетам творческие задания побуждают их приобретать новые знания и быть активными в усвоении материала. Задачи содержат элемент проблемы, помогают кадетам создавать свои индивидуальные задания и находить пути и уровни решения. Элементы демократизации прослеживаются в выборе средств решения проблем, в оценке работы товарищей. Конечно, все это требует от преподавателя дополнительной работы со специальной литературой, дополнительной методической работы по отбору материала, определения места прикладного материала на занятии.
Систематически решая прикладные задачи, кадеты более глубоко усваивают теоретические вопросы, что у них появляется целостное представление о взаимосвязи математики с различными науками и областями знаний. Рассуждения и умозаключения, возникающие в процессе решения задач, способствуют развитию логического мышления, развивают умение кратко, ясно и последовательно выражать свои мысли. Решение прикладных задач также способствует воинскому воспитанию обучаемых, прививает им такие качества, как пытливость, настойчивость, развивает самостоятельность.
В ОКВК я работаю второй год. Осознавая специфику учебного заведения, мне пришлось специально работать над подборкой заданий по военно-прикладной тематике. Каждую такую задачу необходимо было соотнести с конкретной темой в математике, установить уровень усвоения установленной темы для решения данной задачи.
Большую роль в создании военно-прикладной копилки задач послужил совместный с кадетами 4 взвода 1 роты проект по математике «Практическое применение подобия треугольников». В ходе этого проекта кадеты самостоятельно изучили различные методы вычисления расстояния до недоступного объекта, апробировали эти методы, проанализировали преимущества и недостатки метода с точки зрения применения его в военной разведке.
Методическая копилка военно-прикладных задач предложена в приложении.
ПРИЛОЖЕНИЕ.
Тема «Логарифмы».
В момент причаливания корабля к пристани, для того чтобы его остановить, используют следующий прием. С судна на пристань бросают канат, который оборачивают около тумбы, после чего достаточно усилий одного человека, чтобы под действием силы трения остановить даже очень большой корабль. Не вдаваясь в физику, будем считать, что уравновешивание силы корабля и человека происходит по закону F=F0 ·3n, где F - сила корабля, F0 - сила человека, а n - число витков. Найти, сколько витков следует сделать, чтобы человек с приложением силы 8Н смог остановить корабль с силой 120Н.
Совершенно очевидно, что для ответа на поставленный вопрос необходимо найти n из уравнения 120=8.3n : 120=8.3n, 3n=15, n=log315. Теперь, воспользовавшись калькулятором, найдем:
![]() .
.
Полученный математический результат означает, что необходимо сделать 3 (не меньше) оборота каната вокруг тумбы. Разумеется, на практике никто логарифмов не считает, и, как правило, при причаливании корабля человек накручивает количество витков, исходя из своего опыта. Однако это не означает, что так будет всегда: возможно появление нестандартных ситуаций, для того чтобы их спрогнозировать и дать соответствующую рекомендацию, нужны знания, а не только опыт.
Тема «Функции. Графики функций»
1) Отряд разведчиков, выйдя из пункта А, прошел 250 м по азимуту 102°, потом 350 м по азимуту 183°, затем еще 350 м по азимуту 325°.
Проложить маршрут движения разведгруппы. По какому азимуту и сколько метров необходимо пройти отряду разведчиков, чтобы вернуться в пункт А?
2) Сигнальная ракета выпущена под углом 450 к горизонту с начальной скоростью 30м/с. В этом случае высота, на которой находится ракета в определенный момент времени, может быть приближенно вычислена по формуле h=2+21t-5t2. Через сколько секунд ракета окажется на высоте 10 м?
3) На испытаниях нового танка каждые полчаса отмечали в таблице пройденное расстояние.
Проведите прямую по этим данным. Определите чему будет равно расстояние: а) через 6ч после начала движения; б) через 8ч после начала движения; в) через 10ч после начала движения. Запишите уравнение прямой.
4) С двухметровой высоты под углом к горизонту выпущена сигнальная ракета. Изменение высоты ее полета (h,м) в зависимости от времени движения (t,с) описывается формулой h=2+21t-5t2. Используя график, ответьте на вопросы: а) в какое время ракета поднимается на высоту 20м и в какое время она окажется на той же высоте при спуске? б) на какой высоте ракета будет через 3,5 с полета? в) через сколько секунд после начала полета ракета уже была на той же высоте? г) укажите наибольшую высоту подъема ракеты; д) сколько времени потребовалось ракете, чтобы подняться на максимальную высоту? е) Как вы думаете, почему график не доведен до пересечения с осью х?
Тема «Элементы комбинаторики и
теории вероятностей».
1) Стрелок стреляет по мишени. Число попаданий в зависимости от количества выстрелов приведено в таблице:
б) Представьте эту зависимость графически.
в) Болельщики стрелка заключили пари с его соперниками, что, сделав еще 30 выстрелов, стрелок поразит цель не менее 20 раз. Как вы считаете, стоило ли соглашаться соперникам стрелка на пари? Могут ли болельщики стрелка проиграть пари?
2) В отряде 25 бойцов. Двоих надо отправить в разведку. Сколько существует вариантов это сделать?
Тема «Построение треугольника».
Задача. Для определения по карте места нахождения S судна с помощью радиопеленгатора определяют углы SAB и SBA, где А и В береговые радиомаяки, изображённые на карте. Ту же задачу решают с помощью радиолокатора, определяя расстояние от S до А и до В. Как найти на карте месторасположение судна по данным: а) радиопеленгатора, б) радиолокатора?
Решение сводится к построению треугольника:
а) по стороне и двум углам,
б) по трём сторонам.
Тема: "Прогрессии".
1. Десантник, покинув самолет, и до раскрытия парашюта, проходит в первую секунду 4,9 м, а в каждую следующую секунду на 9,8 м больше, чем в предыдущую. Какое расстояние будет пройдено десантником за 5 секунд.
2. Для трансформатора допускается перегрузка в течении 20 мин на 75% от нормального тока. С увеличением времени перегрузки на каждые 20 мин допустимый уровень снижается до 0,8 от предыдущего. Каковы допустимые перегрузки трансформатора, работающего 1, 2, 3 ч?
3. Музыкальная октава делится на 12 равных интервалов - полутонов. Частота каждого последующего звука приблизительно в 1,059 раза больше частоты предыдущего. Во сколько раз нота соль выше ноты до той же октавы.
4. Играют двое. Они поочередно кладут в кучу любое количество камней от 1 до 10. Выиграет тот, кто доведет число камней до 200. Кто победит? И как надо играть, чтобы выиграть (т.е. найти выигрышную стратегию)?
5. Самолет начал снижение на высоте 8000м и в первые десять минут снижался на 500 м в минуту. Запишите формулу для вычисления высоты hn, на которой будет находиться самолет через n минут после начала снижения. С помощью этой формулы определите, на какой высоте будет самолет через 3 мин после начала снижения; через 8 мин. На какой минуте самолет окажется ниже 4000м над уровнем земли?
Изобразите точками координатной плоскости десять членов последовательности(hn).
6. В первый день танковая колонна прошла 10 км. В следующий день колонна прошла 12,5 км. Так в последующие дни колонна проходила на 2,5 км больше. Поход длился 8 дней. Какое расстояние прошла колонна за поход?Дано:
а1=10
а2=12,5
d=2.5
n=8
Решения:
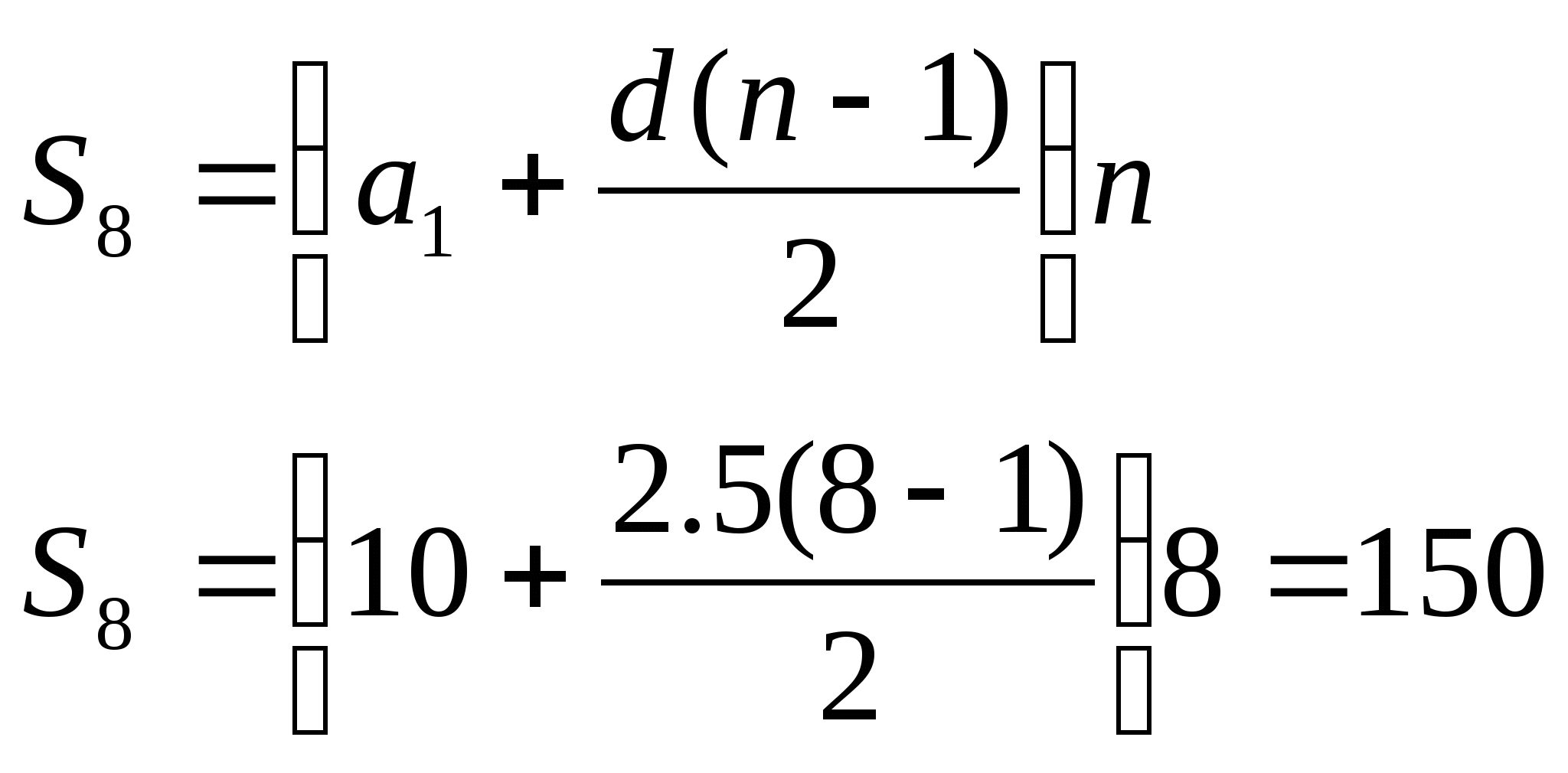
Найти:
S8=?
7. Цех изготавливает каждый день на 2 автомата больше, чем в предыдущий. В течение 5 дней цех изготовил 75 автоматов. Сколько автоматов изготовил цех в 1-й и 5-й дни работы?
8. Подводная лодка за первую минуту погрузилась на глубину 125 метров. В последующие минуты она погружалась в 0,4 раза быстрее предыдущей минуты. Сколько минут лодка будет погружаться на глубину 206,2 метров?
Тема «Квадратные корни».
Сколько требуется синей ленты, чтобы сшить Андреевский флаг?

76 см
46 см
Тема «Решение треугольников».
1) Граната, брошенная при сильном ветре под углом 600 к горизонту, до верхней точки летела 15 м, а приземлилась она в 40 м от бросающего. Найдите, под каким углом к горизонту приземлилась граната.Дано:
![]()
![]() ,ВС=15м,АВ=40м
,ВС=15м,АВ=40м
С

А
В
Найти:
![]()
Решение:
1)![]()
![]()
2)![]()
![]()
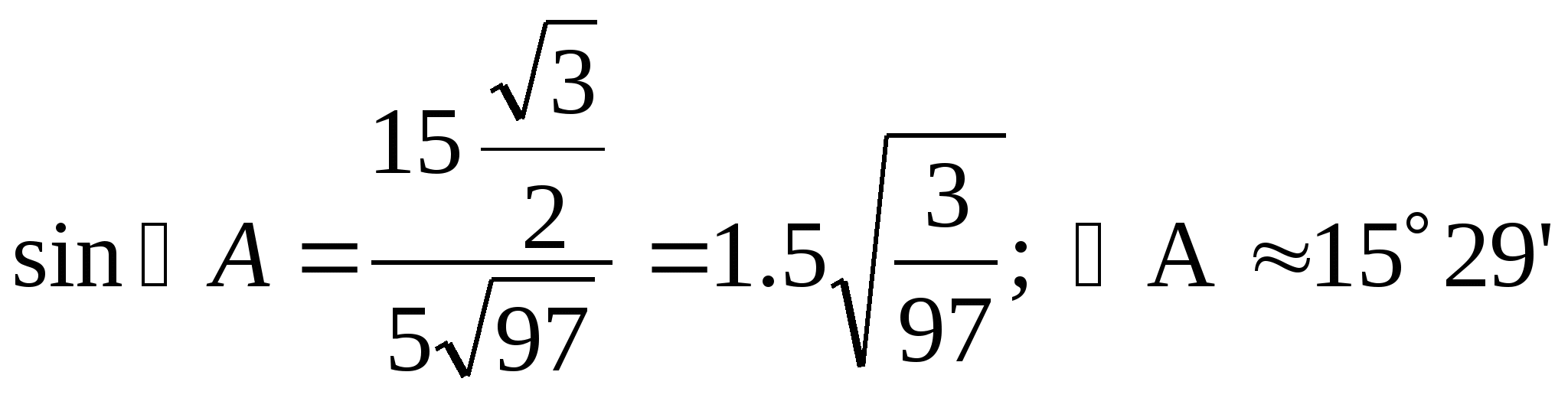
2) Радар засек вражеский самолет на расстоянии 42 км и получил команду уничтожить. При расчете получилось, что для попадания в самолет необходимо запустить ракету под углом 300, так как за время полета ракеты самолет пролетит 24 км. Сколько пролетит ракета до столкновения с самолетом?Дано:
![]()
![]()
ВС=24км,АВ=42км
С

В
А
Найти:
АС=?
Решение:
1) ![]()
2)![]()
3)![]()
Тема «Дифференциальное исчисление функций».
1. Из винтовки выстрелили вверх. Найти закон движения пули, считая, что ускорение земного притяжения 10 м/с2, скорость вылета пули из винтовки 800 м/с. Сопротивлением воздуха пренебречь.
Решение. Ось Ох направим вертикально вверх,
ее начало считаем точкой вылета пули, за единицу длины примем
1м. Ускорение силы тяжести направлено вниз вместе с силой
тяжести. Поэтому в расчетах надо считать ускорение равным
отрицательному числу -10. На основании формулы закон движения
выражается формулой
х=-5t2+C1t+C2. Так как пуля в
момент t=0 имела координату х=0, то 0=0+0+ C2 или
C2=0 поэтому х=-5t2+ C1t.
Чтобы определить C1, возьмем производную от
последней функции. Получим х'=-10t+ C1.
Отсюда, учитывая, что при t=0 производная равна скорости вылета
пули 800 м/с, найдем С1=800, и закон движения пули
имеет вид х=-5t2+ 800t.
2. Окоп противника на расстоянии 1 км виден под углом 0,017
артиллерийских единиц. Какова его длина?
Справка. В артиллерии для измерения углов используется своя система. Круг делится на 60 артиллерийских единиц (а.е.), т.е. 360° = 60 а.е., 6° = 1 а.е.; 0,01 а.е. называется малой единицей. Поэтому угол обозначается так: 3-10 (3 большие единицы и 10 малых). Эту величину легко перевести в градусы: 3,10 • 6°=18.6°
Решение.
Считая расстояние 1000м и длину окопа l
катетами прямоугольного треугольника, получим: l= 1000 • tg α
,где α = 0,017 а.е. = 0,017 • 6° = 0,1° = 6', tg 6' = = 0,017.
Тогда 1 = 17 м. В нашем примере тангенс угла (0,017) совпал со
значением угла в артиллерийских единицах (0,017). Это не
случайность. Именно по этому принципу и выбраны единицы
измерения углов в артиллерии.
Правило. При малых углах линейные размеры (в метрах) предмета,
находящегося на расстоянии 1 км, численно равны значению угла
зрения (в тысячных). Понятно, что если α - угловой размер
предмета в тысячных, а расстояние до него км, то линейный
размер равен l = kα.
С другой стороны, если линейные размеры предмета точно известны
(габариты танка, машины, высота телеграфного столба и т.д.), то
легко найти расстояние до него: k =l/ α. Вот какими чудесными
свойствами обладают артиллерийские единицы измерения углов,
поэтому во время Великой Отечественной войны кадровые
офицеры-артиллеристы делали насечки на козырьке фуражки,
соответствующие тысячным артиллерийской единицы. Тогда можно
грубо оценить угол без
всякого измерительного прибора или узнать расстояние до
предмета, если его размеры известны.
Тема: «Интегральное исчисление функций».
На какую высоту за 10с поднимется ракета, запущенная вертикально вверх, если скорость меняется по закону: V= [2+1/(t+1)2]км/с? Чему равна средняя скорость полета ракеты за этот промежуток времени?
Решение. Путь, пройденный ракетой
за 10с, равен S=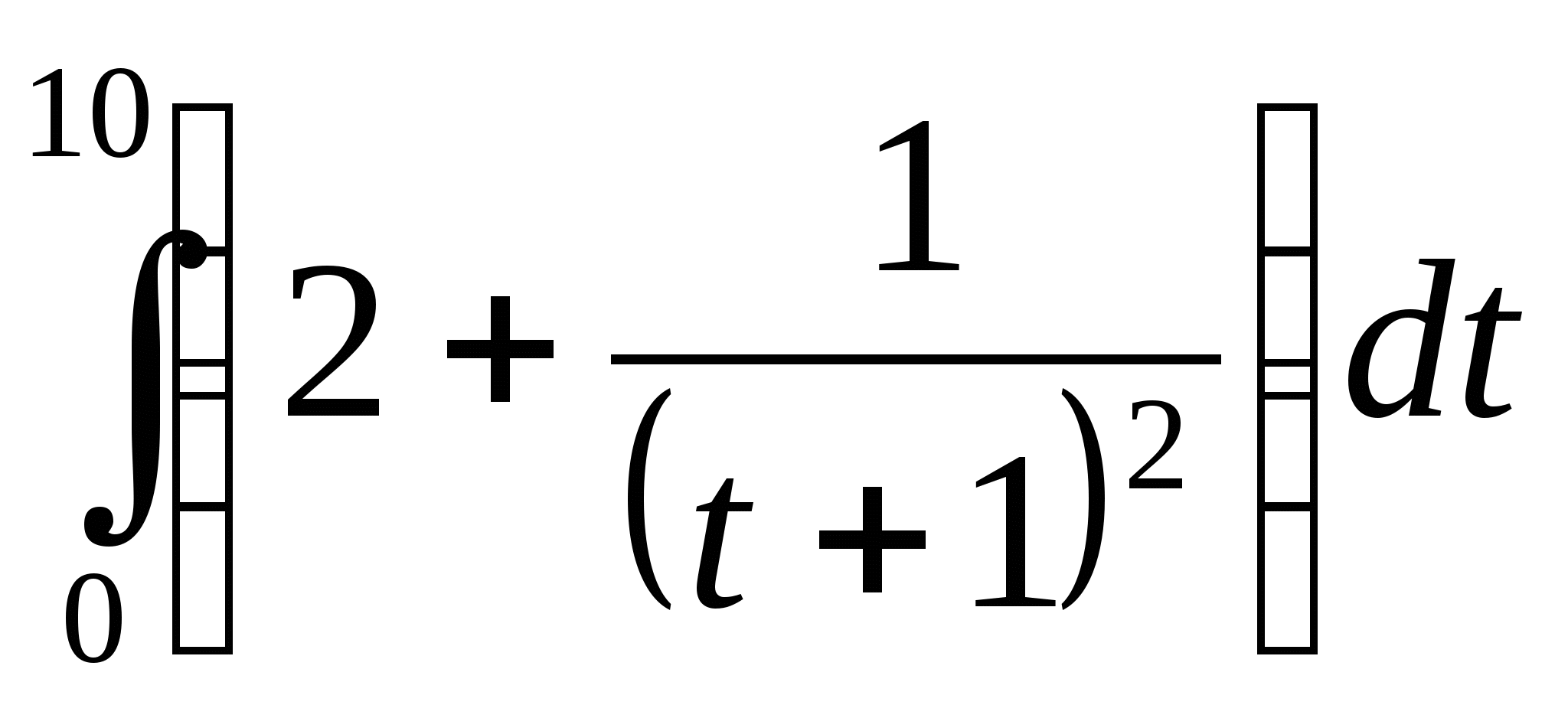 км/с. Функция f(x) = 2+1/(t+1)2 - непрерывная на
[0;10] и принимает положительные значения на этом интервале.
Согласно формуле Ньютона-Лейбница имеем: s=21 км.
км/с. Функция f(x) = 2+1/(t+1)2 - непрерывная на
[0;10] и принимает положительные значения на этом интервале.
Согласно формуле Ньютона-Лейбница имеем: s=21 км.
Поэтому соответствующая средняя скорость ракеты равна: V cр=21/10=2,1км/с.
Ответ: 21км, 2,1км/с.
Тема: "Векторы. Метод координатной на плоскости".
1. На тело действует две равные силы F, причем, угол между ними 1200 и F = 8,3 Н. Найти их равнодействующую.
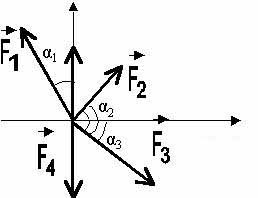
2. Найти величину равнодействующей плоской
системы сил, приложенных к точке О, если F1 = 80 H, F2 = 40 H,
F3 = 60 H, F4 = 40 H, ![]() 1
= 300,
1
= 300, ![]() 2
= 600,
2
= 600, ![]() 3
= 450.
3
= 450.
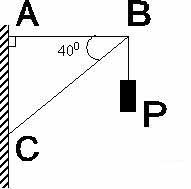
3. К концу кронштейна подвешен фонарь весом P = 20 кг. Найти силу растяжения стержня AB и силу сжатия стержня BC.
4. БМП с огневой позиции А {-1;-1} уничтожила безоткатное орудие В {4;4}. Появляется танк С {-1;3}. Определить угол поворота башни БМП при переносе огня на танк.
5. Найти величину силы, которая совершила работу 150 Дж по перемещению из точки К (-2;3) в точку М (4;-5). Сила направлена вдоль линии движения.
6. При взятии обороны командир отделения указал стрелку огневую позицию в точке В (-4;-1) и сектор ведения огня: справа - точка А (1;-2), слева - точка С (3;0). Определите угол обстрела.
7. Командир минометной батареи получил задачу на уничтожение противника и его огневых средств в районе, ограниченном точками: А (5;4), В (9;6), С (6;7). Какова площадь района обстрела?
Тема: "Соотношения между сторонами и углами треугольника".
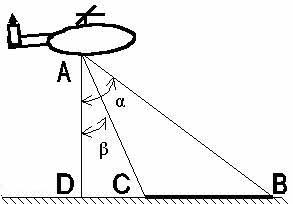
1. С вертолета, летящего горизонтально и
прямолинейно на высоте Н, определены углы ![]() и
и
![]() ,
под которыми видны голова и хвост колонны войск противника,
движущейся по прямолинейному участку маршрута. Определить
глубину колонны, если ее маршрут находится в одной вертикальной
плоскости с траекторией вертолета (Н = 950м,
,
под которыми видны голова и хвост колонны войск противника,
движущейся по прямолинейному участку маршрута. Определить
глубину колонны, если ее маршрут находится в одной вертикальной
плоскости с траекторией вертолета (Н = 950м, ![]() =
810,
=
810, ![]() =
220).
=
220).
2. Подразделение в обороне занимает практически треугольный участок местности. Стороны треугольника равны соответственно 3,8 км , 1,7 км и 2,9 км. Наибольшая сторона треугольника является передним краем обороны. Определить площадь участка обороны в гектарах и его максимальную глубину.

3. В некоторый момент с парохода Р отметили азимуты пунктов А и В на суше. Азимут пункта А оказался 310, пункта В - 850 . По карте установили, что направление АВ-1300, расстояние А = 650 м. Найти расстояние от парохода Р до пункта А в момент измерения углов.
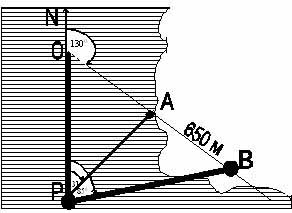
Примечание. Азимут точки А относительно точки В есть угол, вершина которого находится в точке В, одна сторона ВС направлена на север, другая проходит через точку А. Сторона ВА отсчитывается от стороны ВС по движению часовой стрелки.
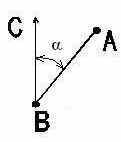
4. Для определения расстояния от
наблюдательного пункта А до центра опорного пункта
подразделения противника В построен треугольник АВС.
Длина АС = 432м, ![]() ,
,
![]() Определить
расстояние от наблюдательного пункта до центра опорного пункта
противника.
Определить
расстояние от наблюдательного пункта до центра опорного пункта
противника.
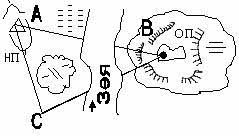
5. В ходе ведения разведки РД № 1 установил
непроходимые участки местности. Для определения расстояния
между пунктами А и В, разделенными непроходимым участком
местности, построен треугольник АВС . Определить расстояние
между пунктами А и В, если АС = 2,8 км, ВС = 3,9 км, ![]() .
.
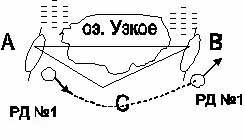
6. Из орудия БМП в засаде необходимо сделать выстрел по движущейся по дороге БМП "Мардер" противника. Скорость цели 40 км/ч и она движется под углом 500 к линии визирования АВ. Определить угол упреждения , который нужно учесть наводчику при прицеливании, если скорость снаряда равна 750 м/с.
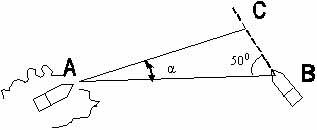
7. Для того, чтобы переплыть реку перпендикулярно ее течению ось плавающей боевой машины пехоты БМП-2 должна составить с направлением АВ1 угол , называемый углом сноса . Найти угол сноса , если собственная скорость БМП-2 равна 10 км / ч, скорость течения реки равна 1,3 м/с. Сколько времени потребуется боевой машине для переправы через реку шириной 920 м.
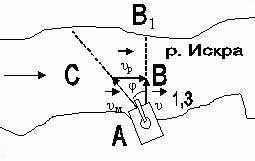
8. Обороняемый участок местности по форме является практически ромбом со стороной 2,3 км и углом равным 1420. Вершина тупого угла направлена в сторону противника. Определить площадь обороняемого участка в гектарах, его ширину по фронту и максимальную глубину.
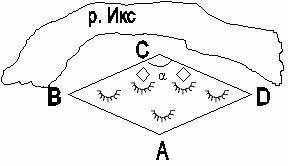
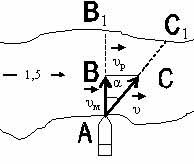
9. Плавающая боевая машина из пункта А на берегу реки движется по реке так, что направление ее оси перпендикулярно течению реки. Определить угол сноса и величину сноса В1С1 боевой машины, если ее собственная скорость равна 8 км/ч, ширина реки 850 м и скорость течения реки 1,5 м/с.
Тема: "Длина окружности и площадь круга".
1. Зона действия радара радиолокационной станции определяется уравнением x2+y2-4x+8y=0. Найти площадь зоны действия радара.
2. По подразделению в районе сосредоточения, занимающему участок RЦ = 1,4 км, нанесен бомбоштурмовой удар авиации. Эпицентр удара удален на 75 м от центра цели. Радиус поражения бомбы равен RП = 600 м. Определить вероятность поражения цели.
Примечание. Эпицентром взрыва называют проекцию точки взрыва бомбы (ракеты, снаряда) на поверхность земли. Радиус поражения - радиус круга с центром в эпицентре взрыва, в любой точке которого цели данного класса поражаются при взрыве бомбы.
Вероятность поражения цели:

3. Взвод занимает опорный пункт 400 м по фронту и 300 м в глубину. По форме опорный пункт можно принять за полукруг. По взводу, поспешно перешедшему к обороне, нанесен огневой удар (залп батареи 155 мм СГ). Условно зону сплошного поражения можно принять за круг с радиусом поражения Rп = 80 м. Найти вероятность поражения личного состава, если точка нанесения удара расположена:
-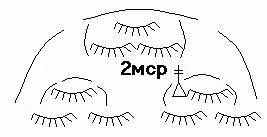 в
середине фронта;
в
середине фронта;
- в центре опорного пункта.
4. Обнаруженный АДН 155 мм СГ занимает
позиционный район, имеющий форму равнобедренной трапеции с
нижним основанием 2,3 км, боковой стороной 1,4 км и угол между
ними ![]() =
630. При расчетах на поражение эту цель заменяют
равновеликой по площади круговой целью. Определить радиус
круговой цели.
=
630. При расчетах на поражение эту цель заменяют
равновеликой по площади круговой целью. Определить радиус
круговой цели.
5. Обнаруженный склад боеприпасов противника занимает участок местности прямоугольной формы по фронту 1,8 км и глубиной 1,2 км. По цели наносится удар управляемой бомбой в кассетном снаряжении. Направление полета бомбы перпендикулярно большей стороне участка, занимаемой целью. Эпицентр взрыва расположен справа и с недолетом от центра цели соответственно на 75 м и 50 м. Определить вероятность поражения цели кассетными боеприпасами, если радиус поражения бомбы равен 400 м.
6. По данным разведки, КП АК, размещенный на местности, занимает участок прямоугольной формы длиной 1,8 км и шириной 1,4 км. По нему нанесен удар авиацией. Направление полета ракет перпендикулярно большей стороне цели. Эпицентр взрыва по направлению практически совпадает с центром цели, недолет - 800 м. Определить нанесенный ущерб (вероятность поражения цели), если радиус поражения удара ракет равен 800 м.
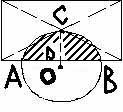
Тема: "Уравнения окружности и прямой".
1. Противник нанес ядерный удар. Граница зараженного участка задана уравнением x2+y2-10x+24=0. Указать на чертеже район заражения, указать его размеры. Попадет ли в зараженную зону колонна танков, движущаяся по маршруту, заданному уравнением: x+y=0?
2. Одна танковая колонна движется по прямой дороге из пункта А (3;2) в пункт В (8;6). Другая колонна танков движется по прямой из пункта С (3;8) в пункт D (-3;2). Определить, куда необходимо отправить транспорт с боеприпасами, чтобы можно было пополнить боекомплект сразу двум колоннам.
3. В трех наблюдательных пунктах, координаты которых А (4;3), В (-3;2) и С (1;-6), одновременно был зарегистрирован звук залпа батареи противника. Установить расположение батареи.
4. Поражаемое пространство от двух гранат определяется линиями: x2+y2-2x-6y+6=0, x2+y2-6x-10y+30=0. Показать на чертеже эти участки, а также найти длину пространства двойного поражения.
Тема: "Многогранники".
1. Сечение траншеи - равнобедренная трапеция, нижнее основание которой равно 90 см, верхнее основание - 1,4 м, боковая сторона - 1,7 м. Определить объем грунта, который нужно вынуть из земли, если общая длина всей траншеи на участке обороны должна быть равна 155 м.
2. Кристалл кварца состоит из правильной 6-угольной призмы с боковым ребром 6,2 см и стороны основания 1,7 см и двух правильных 6-угольных пирамид с боковым ребром 2,5 см. Найти объем кристалла.
3. Армейская палатка представляет собой параллелепипед длиной 5,2 м, шириной 3,6 м и высотой 2,5 м с двускатной крышей, приподнятой на 80 см. Определить объем палатки и количество палаточного материала, необходимого для ее изготовления.
Тема: "Тела вращения".
1. Головная часть ракеты является правильным круговым конусом с диаметром основания 540 мм и образующей, равной 880 мм. Определить объем и площадь боковой поверхности головной части ракеты.
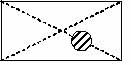
2. В цилиндрический сосуд, наполненный водой до половины, опущен шар диаметром 4 см. Высота сосуда равна 8 см, радиус основания - 2 см. Достигнет ли уровень воды краев сосуда?
3. Земля приблизительно является шаром с радиусом 4,371 км. Определить длину экватора Земли и длину параллели, проходящих через г. Москву и г. Омск.
Тема: "Векторы. Метод координат в пространстве".
1. Орудие, находящееся в точке А (-4;-1;0), подбило танк, расположенный в точке В (-1;-2;0,4). Определить угол, на который необходимо развернуть орудие, чтобы поразить бронетранспортер, находящийся в точке С (3;-2;1).
2. Цель ограничена точками А (1;2;-3), В (0;4;2), С (1;-3;1). Определить количество снарядов, необходимое для полного разрушения цели, если известно, что для полного разрушения 1 ед2 площади цели, необходимо 3 снаряда.
3. К вершине куба приложены 3 силы: F1 =1 H, F2 = 2H, F3 = 3H, направленные по диагоналям граней, выходящих из одной вершины. Определить величину равнодействующей силы.
4. Вычислить работу, производимую силой F {3;-2;-5}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А (2;-3;5) в положение В (3;-2;-1).
Тема: "Уравнение первой и второй степени".
1. Боевой вертолет пролетел некоторое расстояние по ветру за 1ч. 15 мин, сбросил груз и при том же самом режиме работы двигателей пролетел это же расстояние обратно (против ветра) за 1 ч. 45 мин. Определить скорость вертолета в спокойной атмосфере, если скорость ветра равна 20 км/ч.
2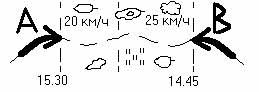 .
В 14 ч. 45 мин подразделение "Синих" вышло из пункта В и
движется в направление пункта А со скоростью 25 км/ч. В 15 ч.
30 мин из пункта А выходит подразделение "Красных" и движется
со скоростью 20 км/ч навстречу подразделению "Синих" с целью
уничтожить его во встречном бою. Определить возможные время и
рубеж встречи подразделений сторон, если расстояние между
пунктами А и В равно 80 .
.
В 14 ч. 45 мин подразделение "Синих" вышло из пункта В и
движется в направление пункта А со скоростью 25 км/ч. В 15 ч.
30 мин из пункта А выходит подразделение "Красных" и движется
со скоростью 20 км/ч навстречу подразделению "Синих" с целью
уничтожить его во встречном бою. Определить возможные время и
рубеж встречи подразделений сторон, если расстояние между
пунктами А и В равно 80 .
3. Колонна войск на втором участке маршрута может двигаться на 15 км/ч быстрее, чем на первом. Длины участков маршрута равны соответственно 60 км и 100 км. С какими скоростями должна двигаться колонна на участках маршрута, чтобы средняя скорость на всем маршруте была равна 25км/ч?
4. В шахту, предназначавшуюся противником для установки баллистической ракеты, бросили без начальной скорости груз, звук от удара которого о дно шахты был услышан через 5 секунд. Определить глубину шахты.
5. Для переправы 124 танков через реку шириной 750 м, имеется 10 переправочных средств. Продолжительность одного рейса переправочного средства - 20 мин, одновременно переправляется один танк. Для сокращения времени переправы танков часть танков можно переправить под водой по одной трассе. Скорость движения танков под водой - 120 м/мин, дистанция между танками - 120 м. Определить минимальное время переправы танков через реку.
Тема: "Функции и их графики".
1. Траектория движения центра масс снаряда приближенно определяется формулой y=0,04x-0,000008x2, где x,y выражаются в м, и начало координат (0;0) - точка вылета снаряда из канала ствола орудия. Определить максимальную дальность полетов снарядов и наибольшую траекторию полета.
2. Зависимость снаряда проводника от времени
описывается формулой ![]() ,
где Q - заряд, Кл, t - время, сек.
,
где Q - заряд, Кл, t - время, сек.
а) найти заряд через 2,5 мин после начала отсчета времени.
б) через сколько минут заряд проводника уменьшится в 2 раза.
3. Средний относительный ущерб Qn
объекта противника при нанесении по нему ряда ударов
однотипными ракетами определяется по приближенной формуле
![]() ,
где n-число ракет. Сколько нужно использовать ракет, чтобы
нанести объекту противника ущерб в среднем 70%?
,
где n-число ракет. Сколько нужно использовать ракет, чтобы
нанести объекту противника ущерб в среднем 70%?
4. Закон движения тела, замедляющего свое движение под действием силы
сопротивления среды, имеет вид ![]() ,
где t - время, сек; x - перемещение, м.
,
где t - время, сек; x - перемещение, м.
а) найти путь, пройденный телом за 20 с после начала замедления
б) через сколько секунд после начала замедления тело пройдет 1,2 км?
Тема: "Производная и ее приложения".
1. Пуля, попадая в твердое тело, движется в
нем по закону ![]() (рис.53-1),
где v0 - скорость, с которой пуля входит в тело.
Найти ускорение движения пули.
(рис.53-1),
где v0 - скорость, с которой пуля входит в тело.
Найти ускорение движения пули.
2. Уравнение траектории полета снаряда в
безвоздушном пространстве имеет вид 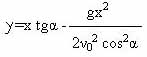 .
При каком значении x, снаряд достигает максимальной высоты.
Вычислить наибольшую высоту полета снаряда, если
.
При каком значении x, снаряд достигает максимальной высоты.
Вычислить наибольшую высоту полета снаряда, если ![]() =
450, v0 = 400 м/с.
=
450, v0 = 400 м/с.
3. Тело массой 2 кг движется прямолинейно по
закону 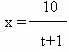 ,
где x - координата, м, t - время, с.
,
где x - координата, м, t - время, с.
а) найти кинетическую энергию тела в момент времени t = 4 с;
б) доказать, что движение замедленное и сила, действующая на тело, пропорциональна кубу расстояния тела до начала координат.
4. Количество электричества, протекающее
через поперечное сечение проводника за промежуток времени [0;t]
выражается формулой ![]() ,
где Q - количество электричества, Кл, t - время, с.
,
где Q - количество электричества, Кл, t - время, с.
а) найти силу тока в конце 8 с;
б) найти наибольшую силу тока за промежуток [1/3;5/6].
5. Из пункта А, находящегося в лесу в 5 км от прямолинейной дороги, разведгруппе нужно попасть в пункт В, расположенный на этой дороге в 13 км от пункта А. По дороге группа может двигаться с максимальной скоростью 5 км/ч, а по лесной - с максимальной скоростью - 3 км/ч. За какое минимальное время разведгруппа сможет добраться из пункта А в пункт В?
6. Стороны прямоугольника изменяются по
закону ![]() ,
где a,b - стороны в см, t - время, с. С какой скоростью
изменяется его площадь в момент t = 3 с?
,
где a,b - стороны в см, t - время, с. С какой скоростью
изменяется его площадь в момент t = 3 с?
7. Лампа висит над центром круглого стола радиуса R. При какой высоте лампы над столом освещенность предмета, лежащего на краю стола будет наилучшей (освещенность прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника света)?
8. Доказать, что из всех прямоугольных треугольников, вписанных в данный круг, наибольшую площадь имеет равнобедренный треугольник.
Тема: "Интеграл и его приложения".
1. При торможении шкив начал вращаться с
угловой скоростью ![]() ,
где w - угловая скорость, рад/с, t - время, с.
,
где w - угловая скорость, рад/с, t - время, с.
а) на какой угол повернется шкив за первые 2 с после начала торможения;
б) за сколько секунд после начала торможения шкив повернется на угол 9 рад?
2. Район, занимаемый противником, ограничен
двумя дорогами, которым соответствует уравнение ![]() .
Найти площадь района, занимаемого противником.
.
Найти площадь района, занимаемого противником.
3.Вычислить работу, которую надо произвести, чтобы выкачать воду из резервуара конической формы с вершиной, обращенной книзу. Резервуар наполнен доверху водой. Радиус основания конуса равен 1 м, высота конуса 2 м.
4. БМП движется со скоростью ![]() .
Найти закон движения, если за время t = 2 c БМП проходит путь
равный 5 м.
.
Найти закон движения, если за время t = 2 c БМП проходит путь
равный 5 м.
5. Два тела начали двигаться одновременно из
одной точки в одном направлении по прямой. Тела движутся со
скоростями ![]() соответственно.
На каком расстоянии друг от друга они окажутся через 5 с?
соответственно.
На каком расстоянии друг от друга они окажутся через 5 с?
6. Для сжатия пружины на 0,02 м необходимо совершить работу 16 Дж. На какую длину можно сжать пружину, совершив работу 100 Дж?