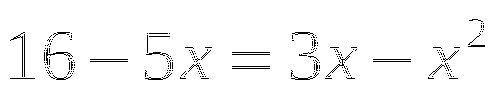Урок на тему Конспект урока по математике для 8 класса «Квадратные уравнения»

Урок на тему «Квадратные уравнения» составила Фанина Ильмира Жаватовна, учительница математики МБОУ СОШ №5 г. Учалы республики Башкортостан.

Тема. «Квадратные уравнения»

Цели урока.

• Сформулировать определение квадратного уравнения.

• Сформировать первичные навыки решения простейших квадратных уравнений.

• Сравнить способы решения квадратных уравнений и уравнений, содержащих неизвестное под знаком модуля.

• Воспитывать навыки ведения научной дискуссии.

• Развивать способность к исследовательской деятельности.

ХОД УРОКА

Актуализация знаний.

Учитель

Учащиеся

1. Продолжите числовую последовательность:

1, 4, 9, 16, 25…..

• _{36, 49, 64….}

1. Какое число стоит на 30 месте, на 41, на n? Почему?

Если вопросы вызывают слишком большое затруднение, то они задаются на дом, с них начинается следующий урок.

• На 30 месте стоит 900, на 41 - стоит 1681, на n месте- 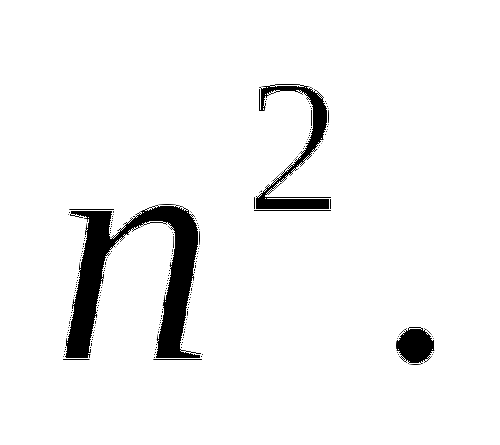т.к. каждое число равняется квадрату места на котором он стоит.

2. На некотором месте стоит число а.

Каким будет предыдущее число, последующее?

с) Какое - то из этих чисел может быть иррациональным числом?

• Предыдущее число равняется

Последующее

• Нет, не может, т.к. любое число а является квадратом натурального числа..

2. Найдите закономерность и назовите следующие пять членов последовательности: _{1, 4, 3, 16, 5, ….}

• _{36, 7, 64, 9, 100…}

• На нечетном месте стоит порядковый номер последовательности , на четном квадрат порядкового номера.

а) Какое - то из этих чисел может быть иррациональным числом?

• Нет, все члены у этой последовательности натуральные числа.

б) Какое число стоит на 101 месте?

• Число 101.

в) Какое число стоит на 102 месте?

• Число 10404.

с) Как по вашему читается выражение , и какие значения может принимать?

• «Икс в квадрате»

• Когда х=0, то данное выражение равен 0

• Когда х и отрицательное и положительное, данное выражение будет принимать только положительные значения.

II. "Открытие" детьми новых знаний.

1. Сформулируйте классификационный признак и разбейте уравнения на группы:

а) б) = в) г)

д)

КОЛЛИЗИЯ!!!

• Все уравнения можно поместить в один класс, неизвестное - 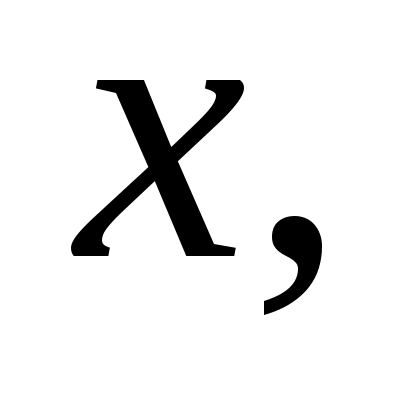параметр -

• Уравнения б), г) - один класс, уравнения с модулем; а) - второй класс, иррациональное уравнение; в), д)- третий класс.

• Уравнения г) и б) - одинаковые, д) и в) -одинаковые, а)- нет.

• Уравнения в) и д) содержит квадрат неизвестного, а другие нет.

Как вы считаете, каково название уравнения в) и д)?

• Наверно, квадратное уравнение.

Назовите тему и цель нашего урока.

• Тема: "Квадратные уравнения", а цель - научиться решать квадратные уравнения.

Сформулируйте определение квадратного уравнения.

КОЛЛИЗИЯ!!!

• Уравнение, содержащее квадрат неизвестного называется квадратным.

• А как же уравнение 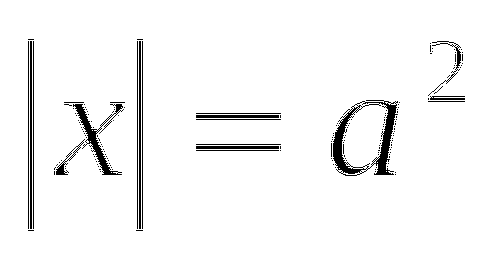??? Оно не квадратное, оно содержит неизвестное в квадрате!

Кто считает по-другому?

• По аналогии с уравнением со знаком модуля, переменная должна быть в квадрате.

• Уравнение, содержащее неизвестное в квадрате, называется квадратным.

2. Решите уравнение:

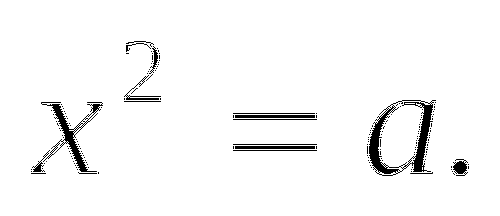
• По определению квадрата, , отсюда получим:

1. Если <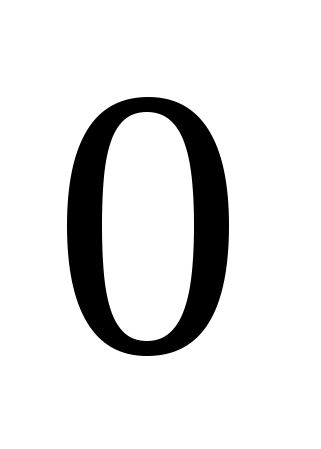, то уравнение решений не имеет;

2. Если , то уравнение примет вид 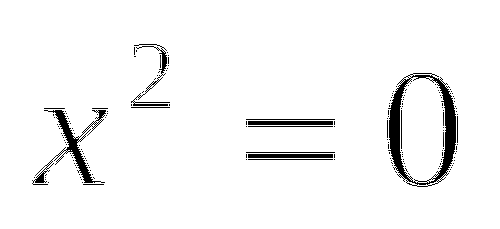и, следовательно, уравнение имеет одно решение ;

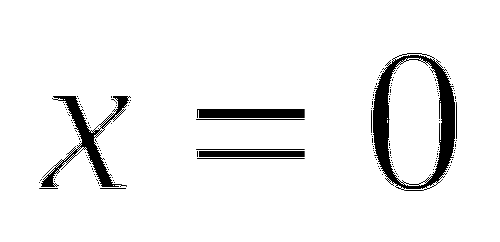3. Если >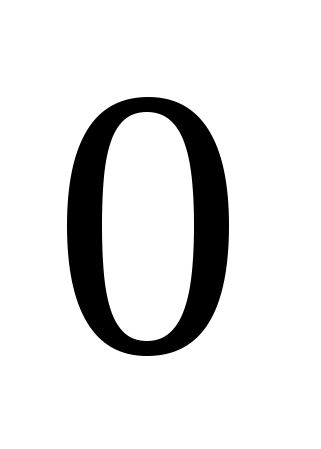, то из обоих частей уравнения можно извлечь квадратный корень, получим уравнение, . (Эта запись на доске остается до конца урока).

3. Что общего между способами решения и решениями уравнени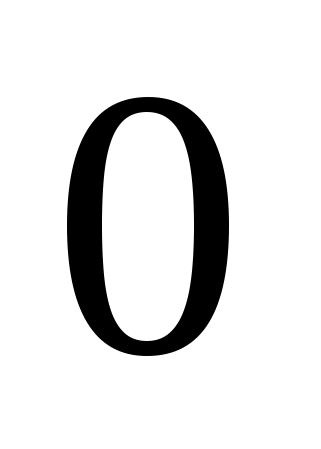й: и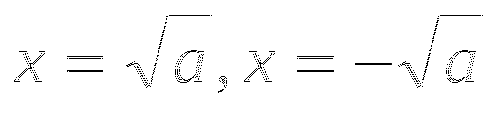

• Оба уравнения решаются методом "уединения", в первом случае квадрата, а во втором модуля и в каждом из них правая часть должна быть неотрицательной.

• Если значение параметра равно нулю, то у обоих уравнений будет по одному решению .

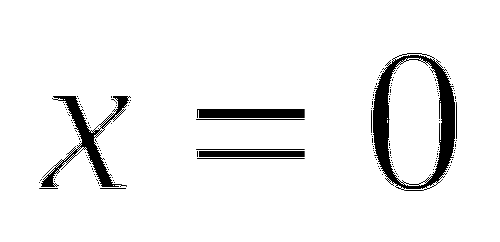III. Рефлексия.

1. Решите устно уравнения:

а) б) в)

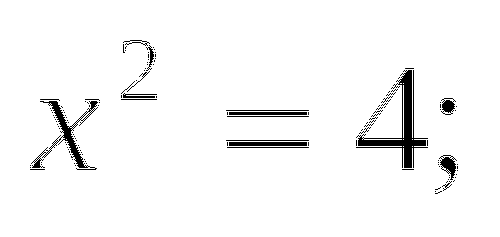• следовательно,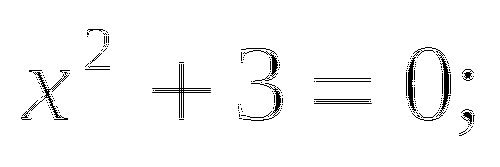

• _{Если перенести 3 вправо, то получится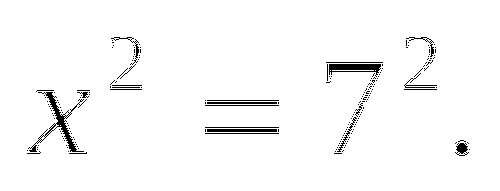} , значит, уравнение решений не имеет.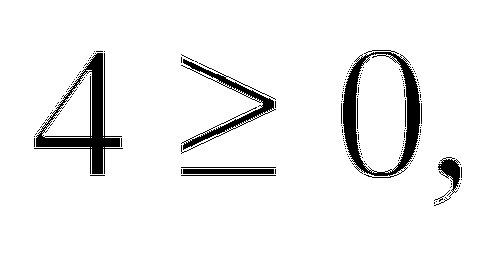

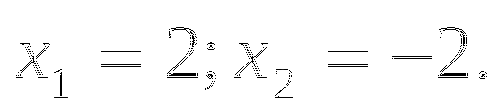• >0 и т.к. квадратное уравнение имеет два решения, отсюда,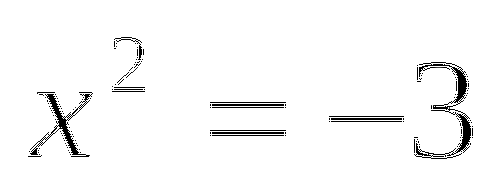

2. Решите уравнения:

а) б)

Кто-то из учащихся решает на доске, остальные - в тетрадях.

х+5=0

х=-5

Ответ: -5.

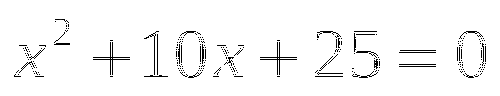
Ответ: 4.

3) Молодцы, ребята! Вы решили два серьезных квадратных уравнения.

Как называется способ, как вы считаете?

КОЛЛИЗИЯ!!!

А как решить следующее уравнение

?

• Наверно, выделение полного квадрата, раз мы выделили квадрат.

• Правая часть не является полным квадратом, как на предыдущих уравнениях.

• Все равно можно выделить полный квадрат ведь 26=25+1

Так как квадрат числа (х+5) не может равняться -1, уравнение не имеет решения.

Молодцы! А как решить уравнение ?

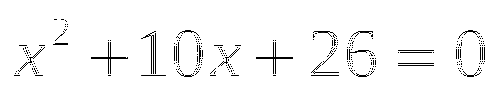
До полного квадрата не хватает двух. Т.к. прибавили 2, то должны и вычесть 2.

3. Решите уравнения

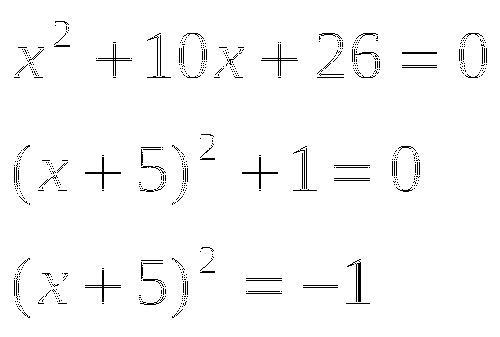
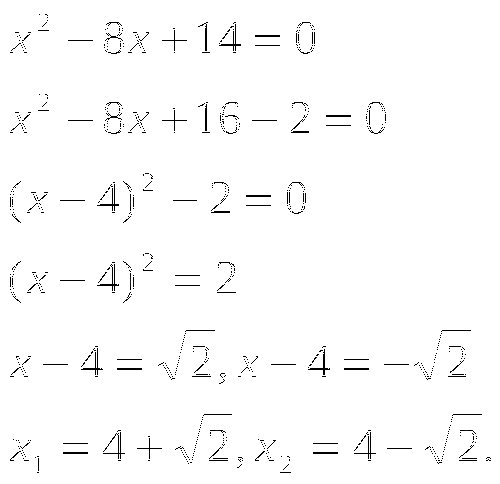
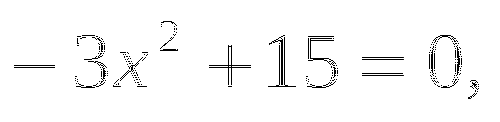
4. Чем отличаются данные уравнения от предыдущих?

В первом уравнений число перед х равен 0, во втором нет свободного числа.

КОЛЛИЗИЯ!!!

5) Как вы думаете как будут называться эти уравнения, раз там не хватают некоторых элементов?

• Квадратные уравнения с недостающими элементами;

• Неполные квадратные уравнения.

6) Тогда как представиться квадратное уравнение в общем виде?

IV. Итог урока. Домашнее задание.

Что нового мы узнали сегодня на уроке?

• Что такое квадратные уравнения и как их решать, виды квадратных уравнений.

• Рассмотрели интересные числовые последовательности.

• Вспомнили, что одни и те же объекты можно классифицировать по разным признакам.

Как вы считаете, достигли ли мы цели сегодняшнего урока?

• Не совсем, мы думаем, что мы рассмотрели не все способы решения квадратных уравнений.

• Этому мы будем учиться на следующем уроке.

Творческое домашнее задание.

Придумайте четыре квадратных уравнения, чтобы одно из них не имело решений, второе имело одно решение, третье - два решения, а четвертое -было неполным.

• А можно пять уравнений придумать?

• Уравнения сдавать на листочках, они будут включены в самостоятельную работу?

Спасибо за урок!!!