Длина окружности. 6 класс.

Тема: Длина окружности.

Тип урока: изучение нового материала.
Цель урока: Опытным путем получить зависимость между длиной окружности и её диаметром.

Задачи урока:

Образовательные:

- вывести формулу длины окружности, применить ее при решении задач;

- получить значение числа π в ходе выполнения практической работы;

- формирование навыков исследовательской деятельности.

Развивающие:

- развивать умения сравнивать, выявлять закономерности, обобщать, делать выводы;

- развивать познавательный интерес учащихся через исторический материал.

Воспитательные:

- прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности.

Формы работы: фронтальная, индивидуальная, парная, взаимопроверка.

Методы обучения: актуализация знаний, практическая работа, использование проблемной ситуации, самостоятельная работа.

Межпредметные связи: история, литература, география.

Сохраняющие здоровье технологии: эмоциональный настрой, построение урока с учётом работоспособности обучающихся, физкультминутка.

Современные образовательные технологии: ИКТ, здоровьесберегающие, проблемное обучение, дифференцированное обучение.

Оборудование: компьютер, проектор, набор кругов из прочного материала и яркого цвета, карандаш, гибкий метр, карточки.

Ход урока.

1. Организационное начало урока.

Проверка подготовленности учащихся и классного помещения к уроку.

2. Постановка цели урока.

Математика - наука древняя, интересная и полезная. Сегодня мы с вами в очередной раз убедимся в этом, и очень хочется, чтобы каждый из вас для себя сделал хотя бы небольшое, но открытие

Создание проблемной ситуации

Постановка проблемы №1. Я сегодня принесла на урок небольшую круглую салфетку. Её радиус 15 см. Хотелось бы обработать её край кружевом, но как узнать, сколько кружев понадобится? Помогите мне, ребята, пожалуйста!

Учащиеся предлагают варианты расчёта.

Постановка проблемы №2. Мой знакомый разбил у себя на даче цветочную клумбу круглой формы. Диаметр её 20 м. Он обратился ко мне за помощью. Сосед просит узнать длину забора, которая получится, чтобы оградить клумбу. Как поступить в данном случае?

Учащиеся предлагают обычно измерить эту длину опытным путём.

Постановка проблемы №3.

-А применим ли этот метод для измерения траектории пути спутника?

Ученики отвечают: «Нет»

-Итак, ребята, сегодня на уроке наша задача найти универсальный способ для нахождения длины окружности, познакомиться с одним удивительным числом и применить наш способ для решения практических задач.

Тема нашего урока: «Длина окружности» запишите в листы, в которых, вы сегодня будете работать.

3. Актуализация опорных знаний.

Нам с вами для успешной работы нужно повторить некоторые геометрические фигуры и понятия, вспомнить правила для округления десятичных дробей до различных разрядов, выполнения умножения и деления десятичных дробей.

1. Давайте вспомним, что мы уже знаем про окружность.

Ответьте на вопросы:

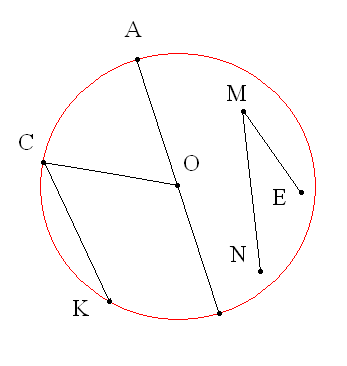
Какой инструмент используется для построения окружности?

Какой буквой обозначен центр окружности?

Как называется отрезок ОА?

Как называется отрезок АВ?

Как связаны радиус и диаметр окружности?

2. Вспомните правило округления десятичных дробей.

Округлите число 62,719 до единиц, десятых, сотых.

3. Вспомните правило выполнения умножения и деления десятичных дробей.

Вычислите устно: 1,2·0,3; 0,45:0,15.

4. Изучение нового материала

Ребята, сейчас перед вами лежит огромная ответственность. Вы будете заниматься исследовательской, научной работой. Вам предстоит открыть неизвестную вам формулу, и от того, как вы поработаете, будут зависеть ваши дальнейшие успехи и успехи ваших товарищей.

Практическая работа (выполняется в парах).

Тема: «Вывод формул для нахождения длины окружности».
Цель: вывести формулу для вычисления длины окружности через диаметр и формулу для вычисления длины окружности через радиус.
Оборудование: набор кругов из прочного материала и яркого цвета, гибкая линейка, микрокалькулятор.

Ход работы:

Выполните следующие действия:

С помощью рулетки измерьте длину окружности.

Сделайте запись С = …

Линейкой измерьте диаметр окружности.

Сделайте запись D =…

Найдите отношение длины окружности к её диаметру (разделите с помощью калькулятора длину окружности на диаметр).

Сделайте запись С : D = ... . Ответ округлите до целых.

Запишите полученные результаты в тетради и на доске.

Данные учащихся обобщаются в таблице:

С - длина окружности

d - диаметр окружности

С : d

1.

2.

3.

Оказывается, какую бы окружность мы ни взяли, частное от деления С на d всегда одно и тоже число. Как вы думаете, о чем это говорит: длина окружности и ее диаметр - прямо пропорциональные величины или обратно пропорциональные?

Прямо пропорциональны, следовательно, чем больше диаметр, тем больше длина окружности, но отношение длины окружности к ее диаметру одно и то же.

Это число обозначают греческой буквой π ( читается «пи»). Значение π с точностью до 12 знаков следующее π ≈ 3,14159265358.

Если округлить значение π до сотых, то получится 3,14. Это значение необходимо запомнить.

π = 3,14

Теперь мы знаем, что С : d = π. Выразим С из этой формулы.

С = πd

Эта формула выражает длину окружности, если известен её диаметр.

В начале урока мы отметили, что диаметр окружности вдвое больше её радиуса.

Как, учитывая это, можно записать формулу ? (создана небольшая проблема)

Записываем: С = 2πr

Эта формула выражает длину окружности, если известен её радиус.

Вывод: закончите предложение «Длину окружности можно найти по формулам……..».

VI. Первичное осмысление и применение изученного.

1.Решите задачу.

Найти длину окружности, радиус которой равен 10 м.

Оформление:

Дано: r = 10 м , π = 3,14

Найти: С - ?

Решение: С = 2πr = 2·3,14·10 = 62,8 (м)

Ответ: С = 62,8 м.

2. Решение проблемы, поставленной в начале урока. Как вы думаете, зачем нам нужно знать формулы длины окружности? (Ученики высказывают свои предложения, приходим к выводу, что бывают ситуации, когда практически затруднительно измерить длину окружности).

3. №847 (решают 2 ученика на обратной части доски; остальные на месте, потом проверяем решение).

r = 24см, π = 3,14

С = 2πr = 2 · 3,14 · 24 = 150,72(см)

Ответ: 150,7 см

r = 4,7 дм, π = 3,14

С = 2πr = 2 · 3,14 · 4,7 = 29,516(дм)

Ответ: 29,516 дм.