Методическая разработка по алгебре на тема Метод рационализации

5

Метод рационализации

Учитель математики МБОУ лицей г.Владикавказ

Сатцаева Нонна Ефимовна

Нередко в заданиях ЕГЭ типа 15 (С₃) требуется решить неравенство, которое сложно поддается обычному методу интервалов: корни не всегда очевидны, а вычисление значений функции в промежуточных точках может оказаться довольно трудоемким процессом.

Есть метод сведения неравенств к неравенствам для рациональных функций, которые решаются, как правило, существенно проще. Речь идет о методе рационализации. Решение этим методом неравенств сэкономит время и снизит риск вычислительной ошибки.

Метод рационализации - это весьма мощная процедура, позволяющая в определённых случаях упростить неравенство и свести его к рациональному неравенству (которое решается методом интервалов).

Рассмотрим, как свести действия, по замене одного выражения другим практически до автоматизма, как обойтись без лишних технических «заморочек» и детального анализа выражения каждого типа.

1. Рассмотри неравенство с модулями. (можем взять любой знак)

Так как модуль определен для любого числа, то говорить о области допустимых значений не нужно.

Умножим обе части данного неравенства на положительное число

Перед нами разность квадратов

, так как ,

, т.е.

Итак, равносильно

Пример:

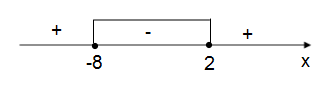
Ответ:.

Пример 2.

Запишем в виде разности

,

, при любом значении х,

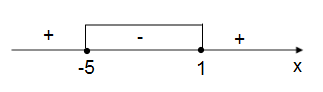
Ответ: .

Рассмотрим случай, когда в выражении , тогда _{и .}

_{Рассмотрим неравенства следующего вида . Начнем с области допустимых значений.}

_ОДЗ:

_{Умножим обе части на сумму корней :}

Итак, _{равносильно}

_{Пример.};

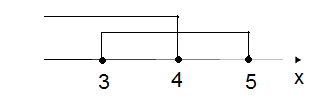
Ответ: .

Пример.

ОДЗ:

Преобразуем числитель дроби:

Знак числителя будет совпадать со знаком разности:

т.е. со знаком

Аналогично, преобразуем знаменатель дроби. Знак знаменателя дроби совпадает со знаком разности

Итак, исходное неравенство равносильно неравенству :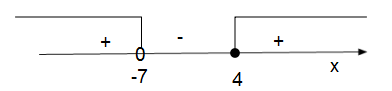

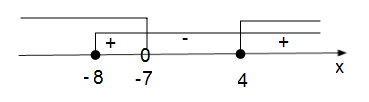
С учетом ОДЗ:

Ответ:

Рассмотрим следующий тип неравенств, которые можно решить методом рационализации.

. ОДЗ:

Решаем обычным способом.

Перепишем в виде

Заметим, что разности и ,должны быть одновременно либо меньше нуля, либо больше нуля. Это возможно только в том случае, если произведение этих разностей будет строго больше нуля. То есть:

Замечание. В исходном неравенстве знак >0, и в замене знак >0. Если бы в

исходном неравенстве был бы знак <0, то и в замене был бы <0.

Итак: .

Частный случай:

1. пусть , т.е. .

Итак,

Пример. ОДЗ:

Преобразуем числитель дроби:

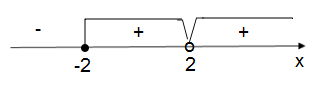
Ответ:

Пример: .

ОДЗ:

Перепишем неравенство в виде: , знак данного неравенства совпадает со знаком следующего

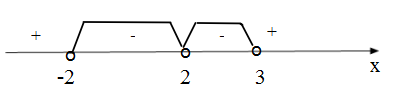
Данный промежуток входит в ОДЗ.

Ответ: .

Следующий тип неравенств: логарифмические неравенства.

ОДЗ:

Решим обычным способом.

Замечание. В исходном неравенстве знак >0, и в замене знак >0. Если бы в

исходном неравенстве был бы знак <0, то и в замене был бы <0.

Итак: , где

Частные случаи:

1. ; , где

Итак: .

2. , ,где

Итак:

3. , , где

Итак:

4. , где

Пример: .

ОДЗ: .

Знак данного неравенства совпадает со знаком следующего неравенства:

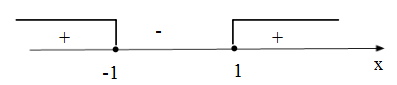
С учетом ОДЗ: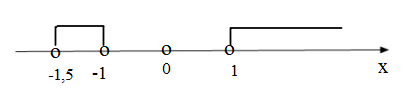

Ответ: .

Пример: .

ОДЗ:

Преобразуем исходное неравенство

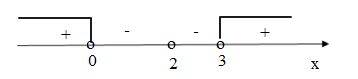
С учетом ОДЗ: .