Конспект урока по геометрии на тему Скалярное произведение векторов (9 класс)

Урок «Скалярное произведение векторов»¹

Цель: познакомить учащихся со скалярным произведением векторов, его свойствами и показать, как применяется скалярное произведение векторов при решении геометрических задач.

Демонстрации: презентация «Скалярное произведение векторов»

Опорный конспект

Ход урока.

1. Повторение ранее изученного материала о свойствах векторов.

   1. Повторение свойств векторов:

      • Определение вектора²

Вспомним свойства векторов³

• Координаты вектора с концами в точках A(x_A, y_A) и B(x_B, y_B) определяются по формуле:

• Длина вектора

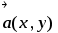
• Координаты суммы векторов a(x_A, y_A) и b(x_B, y_B) :

• Координаты произведения вектора a(x, y) на число λ:

1. 1. 1. 2. Диктант на вычисление координат и длины вектора⁴:

Даны точки A(2; -3), B(-1; 2), С(0; -4)

1. Найдите координаты вектора AB

2. Найдите координаты вектора ВС

3. Найдите длину вектора AB

4. Найдите длину вектора BC

5. Произведение 5 · AB:

1. 1. 1. 1. Самопроверка диктанта по доске с выставлением оценки (по количеству правильно выполненных заданий)⁵

1. 1. 1. 1. Выставление оценки

2. Объяснение нового материала.

1) Рассмотрим понятие угла между векторами⁶

• • Любые 2 вектора - и можно построить из одной точки.

  • Углом между ненулевыми векторам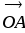и и 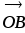называется угол AOB

  • Углом между любыми двумя ненулевыми векторами и называется угол между равными им векторами с общим началом.⁷

  • Если векторы параллельны или один из них равен нулю, то угол между ними считается равным нулю.⁸

Примеры⁹:

, , , , ,

, если α = 90⁰

2) Обучающиеся записывают в тетрадях: Скалярным произведением векторов называется произведение их длин на косинус угла между ними¹⁰:

5) Примеры: (первые 2 примеры учитель вычисляет сам, остальные - обучающиеся с проверкой по доске)

1. , ,

2. , ,

3. , ,

4. , ,

5. , ,

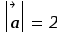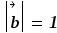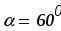
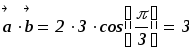
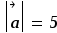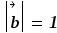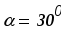
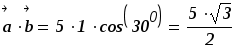
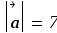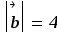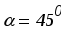
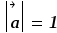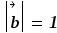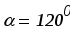
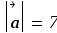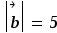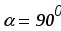
4) Свойства скалярного произведения¹¹: (обучающиеся записывают в тетрадях).

I.

,

II.

III. ,

IV. , то

V¹².

VI.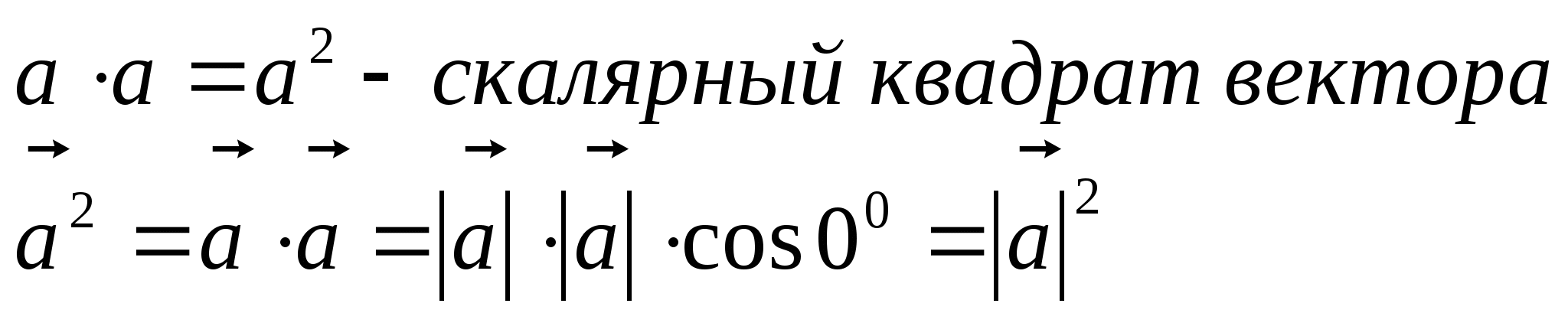

5) Скалярное произведение векторов в координатах: Скалярным произведением векторов¹³ и называется число

Примеры¹⁴:

6) Диктант на закрепление вычисления скалярного произведения в координатах¹⁵:

Вычислите скалярное произведение векторов:

1. 1. a(1,1); b(1,2)

   2. a(-2,5); b(-9,-2)

   3. a(-3,4); b(4,5)

   4. a(5,2); b(-9,4)

   5. a(-1,1); b(1,1)

самопроверка по доске¹⁶ с выставлением оценки.

7) Итак, из вышеизложенного вытекают 2 очень важных следствия¹⁷:

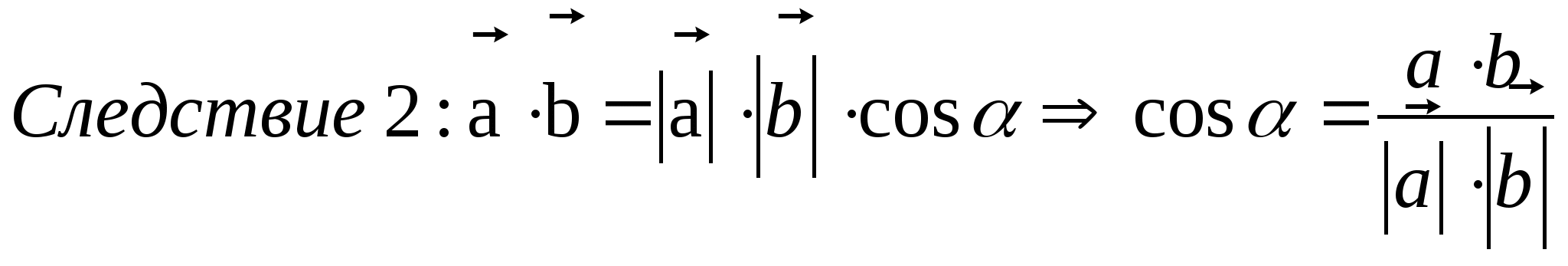
8) Примеры¹⁸: Даны 2 вектора: и

Вычислите:

1. 

2. 

3. 

4. 

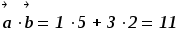
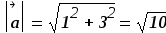
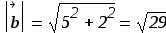
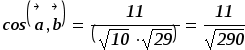
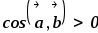5. , значит угол острый

9) проверка ответов.¹⁹

10) Второе следствие позволяет важнейшую операцию нахождения угла между векторами свести к нескольким простым действиям²⁰:

Вычисление угла между векторами с координатами:

a (a₁, a₂), b (b₁, b₂)

1. Вычислить скалярное произведение векторов:

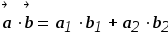
2. Вычислить длину вектора a:

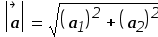
3. Вычислить длину вектора b:

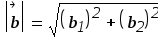
4. Найти произведение длин векторов:

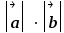
5. Разделить скалярное произведение векторов на произведение их длин:

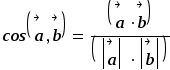
3. Домашнее задание: §§101 - 103, вопросы №№ 13 - 18. (Л.С. Атанасян, В.Ф. и др. «Геометрия 7 - 9» «Просвещение». 2008 г.), №№ 1044 (в), 1047 (в), 1048 (для углов В и С), 1066.

Приложение

1 Слайд 1 - тема урока

2 Слайд 2 - Вектор - направленный отрезок

3 Слайд 3 - свойства векторов

4 Слайд 4 - диктант - действия 1-6

5 Слайд 4 - действия 7-11

6 Слайд 5 - действия 1-8

7 Слайд 5 - действия 9-11

8 Слайд 5 - действие 12

9 Слайд 6

10 Слайд 7

11 Слайд 9

12 Слайд 10

13 Слайд 11

14 Слайд 12

15 Слайд 13 - действия 1-6

16 Слайд 13 - действия 7-11

17 Слайд 14

18 Слайд 15 - действия 1-5

19 Слайд 15 - действия 6-11

20</ Слайд 16

6