Занятие кружка в 10 классе на тему «Нахождение расстояния между скрещивающимися прямыми пятью способами на примере решения одной задачи».

1. Занятие кружка в 11 «А» классе.

Тема: «Нахождение расстояния между скрещивающимися прямыми пятью

способами на примере решения одной задачи».

Цель: 1) Рассмотреть 5 способов решения классической задачи на нахождение расстояния между диагоналями соседних граней единичного куба.

2) Развитие навыка у учащихся подходить к решению задач с разных точек зрения.

3) Снять неуверенность учащихся при решении стереометрических задач.

4) прививать интерес к математике.

5) Готовить учащихся к ЕГЭ по математике.

Ход занятия.

Задача. Найти расстояние между диагоналями А₁С₁ и АD₁ в единичном кубе.

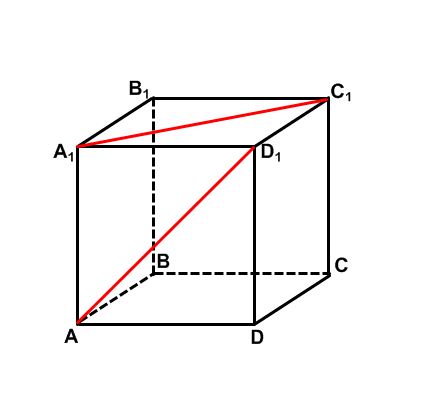
1-й способ: Метод нахождения длины общего перпендикуляра двух скрещивающихся прямых.

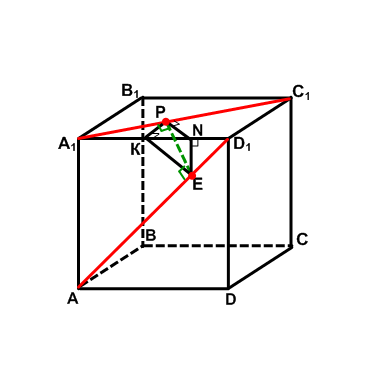
Пусть РЕ - общий перпендикуляр скрещивающихся прямых А₁С₁ и АD₁. Проведем

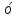ЕN А₁D₁, РК А₁D₁. Тогда РN - проекция наклонной РЕ на пл. А₁В₁С₁, по теореме о трех перпендикулярах РN 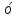А₁С₁. КЕ - проекция наклонной РЕ на пл. А₁D₁D, аналогично

КЕ 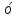АD₁.

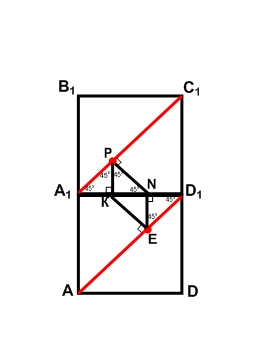
Рассмотрим отдельно развертку граней. А₁КР равнобедренный, 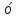А₁РК = 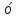КРN =

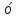= РNК = 45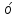. Тогда РКN - равнобедренный, А₁К = КN. Аналогично из нижнего рисунка ND₁ = KN, отсюда следует, что А₁К = КN = ND₁=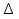

Найдем РN из треугольника КРN: РN =

Из треугольника РNЕ РЕ = Ответ:

2-й способ: Нахождение расстояния от одной из скрещивающихся прямых до параллельной ей плоскости, проходящей через другую прямую.

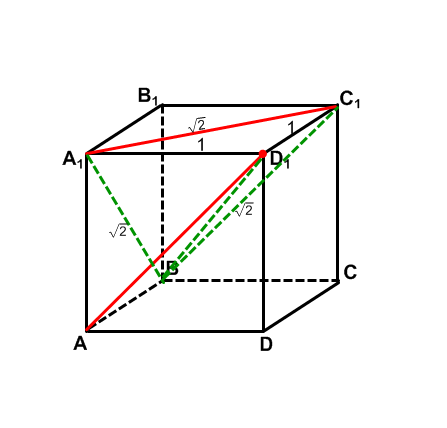
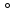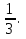Проведем ВС₁ АD₁, АD₁ ВС₁, ВС₁пл.А₁ВС₁ АD₁ 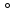пл.А₁ВС₁. Найдем расстояние от прямой АD₁ до этой плоскости, например, от точки D₁ до этой плоскости. У нас получилась пирамида D₁А₁ВС₁. Ее объем можно найти двумя способами.

V = 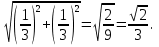, если за основание принять 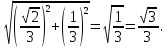₁С₁В, h - искомое расстояние.

V = 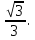ВВ₁, где ВВ₁ - высота, проведенная к основанию А₁ВС₁.

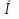
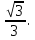ВВ₁, откуда h = Ответ: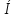

3-й способ: Нахождение расстояния между двумя параллельными плоскостями, проходящими через данные скрещивающиеся прямые.

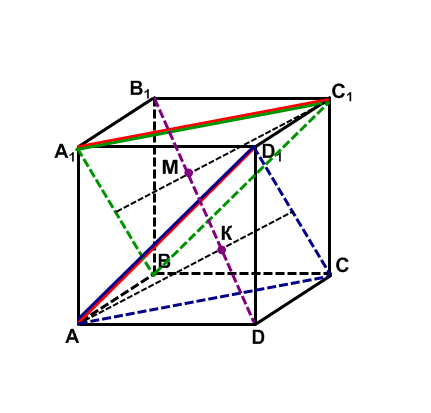
Проведем С₁В D₁А и АС А₁С₁, тогда пл. А₁С₁В пл. АD₁С, т. к. две пересекающиеся прямые одной плоскости параллельны соответственно двум пересекающимся прямым другой плоскости. Найдем расстояние между этими параллельными плоскостями, оно и будет расстоянием между скрещивающимися прямыми.

Проведем диагональ В₁D, она перпендикулярна нашим плоскостям и пересекает их в точках М и К. Эти точки делят диагональ В₁D на 3 равные части. Это видно на отдельном рисунке (теорема Фалеса).

Расстояние между плоскостями - длина отрезка МК. МК = 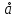В₁D =

Ответ: .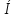

4-й способ: Метод «экрана». Нахождение расстояния от точки, являющейся проекцией одной из скрещивающихся прямых на перпендикулярную ей плоскость (так называемый «экран») до проекции другой прямой на ту же самую плоскость.

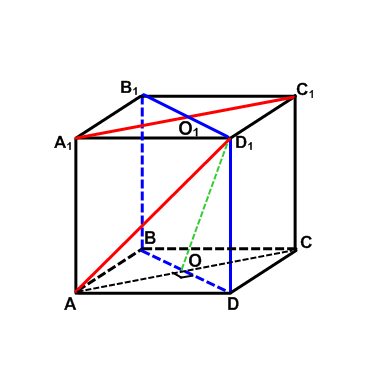
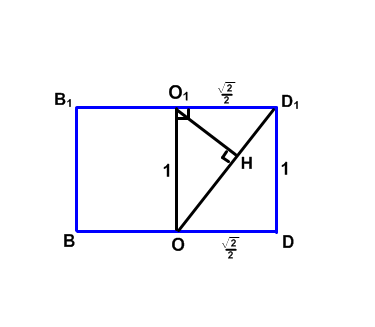
В качестве «экрана» возьмем плоскость В₁D₁D (на рисунке - синяя).

Проекцией прямой А₁О₁ на эту плоскость будет точка О₁, проекцией прямой АD₁ будет прямая ОD₁. Найдем расстояние от точки О₁ в плоскости DВВ₁ до прямой ОD₁, т. е. отрезок О₁Н.

ОD₁ = 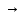По свойсвам пропорциональных отрезков в прямоугольном треугольнике ; ;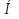

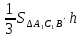
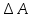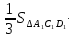Из треугольника О₁НD₁ по теореме Пифагора находим О₁Н =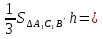

Ответ: .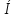

5-й способ: Нахождение расстояния между скрещивающимися прямыми с помощью координат.

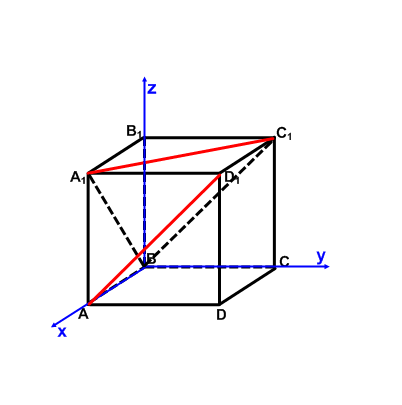
Введем систему координат, выбрав за начало координат точку В, ось абсцисс направим по лучу ВА, ось ординат - по лучу ВС, ось аппликат - по лучу ВВ₁. За единичный отрезок выберем длину стороны куба.

Проведем ВС₁ 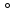АD₁, ВС₁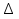пл.А₁ВС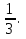₁ АD₁ 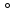пл. А₁ВС₁. Найдем расстояние от прямой АD₁ до этой плоскости, например, от точки А до этой плоскости.

А(1; 0; 0).

Запишем уравнение плоскости А₁ВС₁ (назовем ее 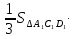в общем виде: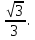

А₁(1; 0; 1); С₁(0; 1; 1); В(0; 0; 0). Все точки принадлежат искомой плоскости, значит, их координаты удовлетворяют уравнению плоскости, подставим их, при этом d = 0, т. к. плоскость проходит через начало координат.

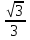
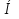Подставляем эти коэффициенты в уравнение.

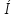, разделим обе части на с.

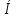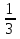, т. е.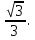

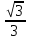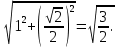= , где А(х₀; y₀; z₀).

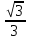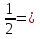= = Ответ: .

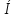Подведение итогов.