Конспект урока алгебры Координаты вектора (9 класс)

План-конспект урока геометрии 9 класс

Учитель: Воропаева Галина Викторовна

Тема урока. Координаты вектора.

Цель урока: Формирование понятия координат вектора и умения применять изученные определения и свойства к решению задач,воспитывать аккуратность при выполнении чертежей, развивать интерес к теме урока

Тип урока: Урок объяснения нового материала

Наглядность: Таблица «Координаты вектора», презентация «Координаты вектора» , компьютер, проектор

Методы обучения: словесный, наглядный, практический.

Формы работы: фронтальная, работа с учебником, самостоятельная, устная.

Ход урока

I. Организационный момент

Сообщение темы и цели урока.

слайд №1

II. Проверка домашнего задания

Проверить наличие выполненного домашнего задания, ответить на возникшие вопросы учащихся.

Устный опрос:

1. Дайте определение вектора.

2. Объясните, какой вектор называется нулевым.

3. Что называется длиной ненулевого вектора?

4. .Чему равна длина нулевого вектора?

5. Какие векторы называются коллинеарными?

6. Дайте определение равных векторов.

7. Объясните смысл выражения: «Вектор отложен от точки А».

8. Сколько разных векторов, равных данному, можно отложить от заданной точки

9. Два коллинеарных вектора направленные одинаково называются...

10. Векторы называются равными, если…

III. Изучение нового материала

Из курса алгебры известно понятие декартовой системы координат. Для задания прямоугольной системы координат необходимо:

1) Провести две взаимно перпендикулярные прямые, на каждой из которых выбрать направление (изображается стрелкой);

2) Выбрать единицу измерения отрезков. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.

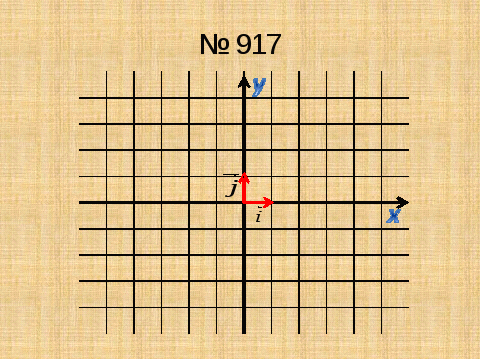
Отложим от начала координат О единичные отрезки (т. е. векторы, длины которых равны единице) так, чтобы направление вектора совпало с направлением оси .

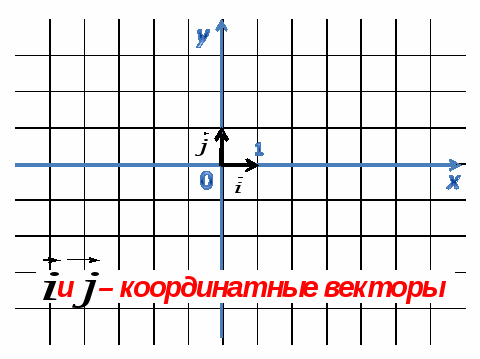слайд №2

Эти векторы назовем координатными векторами.

Координатные векторы не коллинеарны, поэтому любой вектор можно разложить по координатным векторам, причем коэффициенты разложения (числа х и у ) определяются единственным образом.

Определение. Координатами вектора в данной системе координат называются

коэффициенты его разложения по координатным векторам.

Запись координат вектора: .

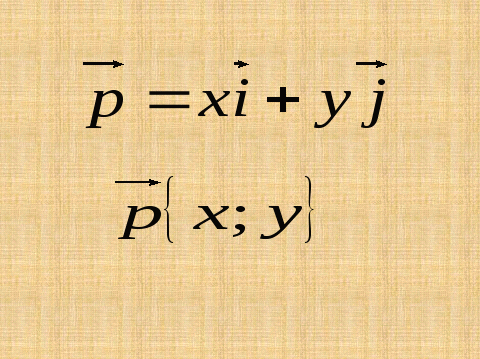
слайд №3

Коэффициенты разложения вектора р по координатным векторам называются координатами вектора р в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора. На рисунке вектор , и вектор (слайд 6).

Так как нулевой вектор можно представить в виде

, то его координаты равны нулю:

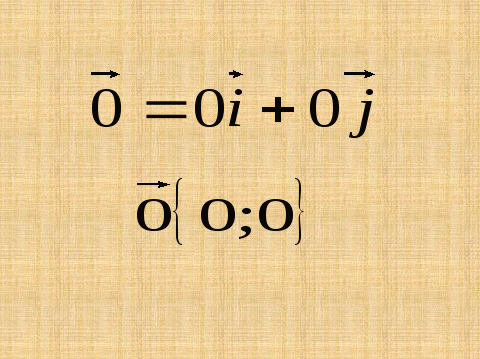
Координаты равных векторов соответственно равны.

слайд №6

Примеры определения координат векторов (слайды 7, 8, 9)

Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число (слайд 10).

1. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

слайд № 10

2. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

слайд №11

Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

слайд №11

IV. Закрепление новых знаний и умений учащихся

1. Работа с учебником

Учащимся предлагается найти в тексте учебника п. 89 (стр. 224 - 226) ответы на вопросы:

1) Что такое координаты вектора?

2) Чему равны координаты координатных векторов?

3) Как связаны между собой координаты равных векторов?

4) Сформулировать правила нахождения суммы, разности векторов, произведения вектора на число.

2. Устная работа на закрепление новых знаний и умений.

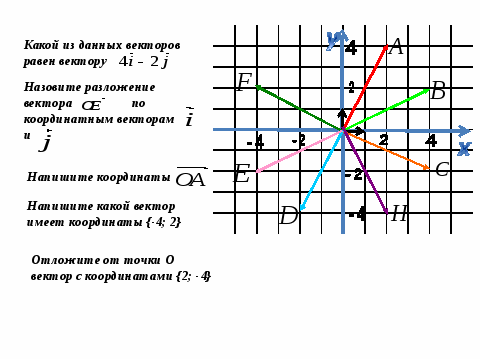
слайд №12

3. Решение заданий из учебника с помощью интерактивной доски и самостоятельно.

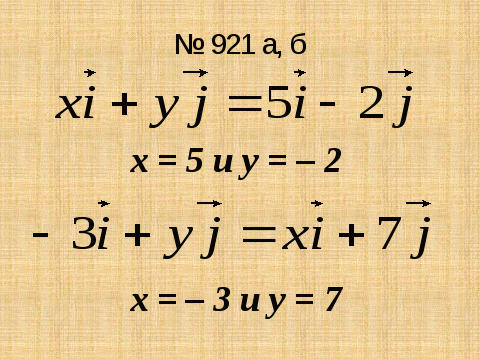
слайды №13, №14. №15

4. Решение упражнений на доске и в тетрадях

№ 922 (а, б); № 923 (в, г).

V. Задание на дом

п. 89 (стр. 224 - 226) № 920 (в); № 921 (г); № 922 (г); № 923 (б)

Учитель проводит инструктаж по выполнению домашнего задания

VI. Итог урока

Учитель вместе с учащимися подводят итог урока, выставляет оценки, комментирует их.