Решение тригонометрических уравнений, сводящихся к квадратным. Урок 6

Урок 6

Тема. Решение тригонометрических уравнений , сводящихся

к квадратным уравнениям.

Цель. Выработать у уч-ся умения и навыки решения тригонометрических уравнений , которые сводятся к квадратным относительно тригонометрических функций.

Ход урока.

1.Сообщить результаты самостоятельной работы и проанализировать её.

2. Индивидуально:sin ( x + 4 ) = 0,5

x + 4 = (-1)^k + pk , kÎ Z ;

х = - 4 + (-1)^k + pk , kÎ Z ;

Ответ : -4+ (-1)^k + pk , kÎ Z .

б) 2 Sin x - 1 = 0

2 Sin x = 1

Sin x =

х = (-1)^k + pk , kÎ Z ;

Ответ : (-1)^k + pk , kÎ Z .

в) sin ( 4x - ) = 0

4x - = pk , kÎ Z ;

4x = + pk , kÎ Z ;

х = + , kÎ Z ;

Ответ : + , kÎ Z .

г) sin( - 3x ) - = 0 ;

-sin( 3x - ) =

3x - = (-1)^k arcsin (-) + pk , kÎ Z ;

3x = + ( - 1)^k+1 + pk , kÎ Z ;

x = + ( - 1)^k+1 + , kÎ Z ;

Ответ : + ( - 1)^k+1 + , kÎ Z.

д) tg ( 4 - x) = -1;

tg ( - x) = -1;

- tg x = -1;

x = arctg 1 + pn , nÎZ;

x = + pn , nÎ Z ;

Ответ : + pn , nÎ Z .

е) 4 sin x cos x = 1

2 Sin 2x = 1

Sin 2x =

2x = (-1)^k arcsin () + pk , kÎ Z ;

2x = ( - 1)^k + pk , kÎ Z ;

x = ( - 1)^k + , kÎ Z ;

Ответ : ( - 1)^k + , kÎ Z .

Устно:

решите уравнения:

а) sin x = 0

б) cos x = 1

в) tg x = 0

sin x = 1

cos x = -1

tg x =

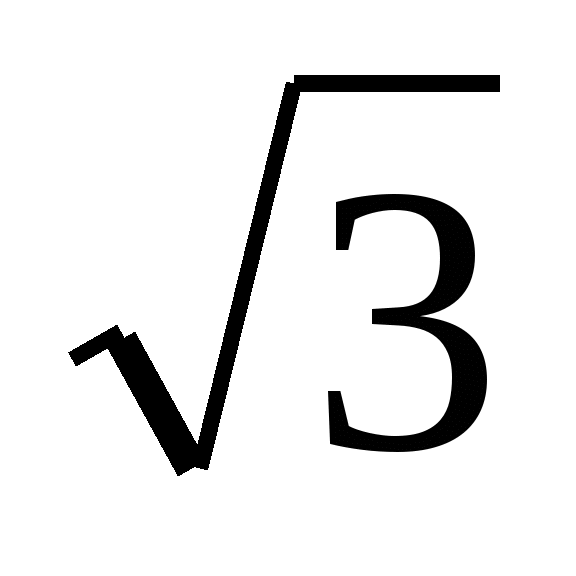
sin x = -1

cos x = 0

tg x = 1

3. На практике часто встречаются тригонометрические уравнения, которые содержат в себе тригонометрические функции в различных степенях или различные функции одного и того же аргумента. Специального алгоритма решения тригонометрических уравнений нет. Но среди них есть такие, которые сводятся к простейшим решением квадратных уравнений относительно тригонометрических функций.

Как решаются такие уравнения?

Сегодня рассмотрим их решения.

Сообщаю тему и цель урока.

Например: cos 2x + sin x = 0

Решение.

cos² x - sin² x + sin x = 0

1 - sin²x - sin²x + sin x =0

2sin²x - sin x - 1 = 0

Пусть sin x = t , тогда

2t² - t - 1 = 0

t₁ = 1; t₂ = -.

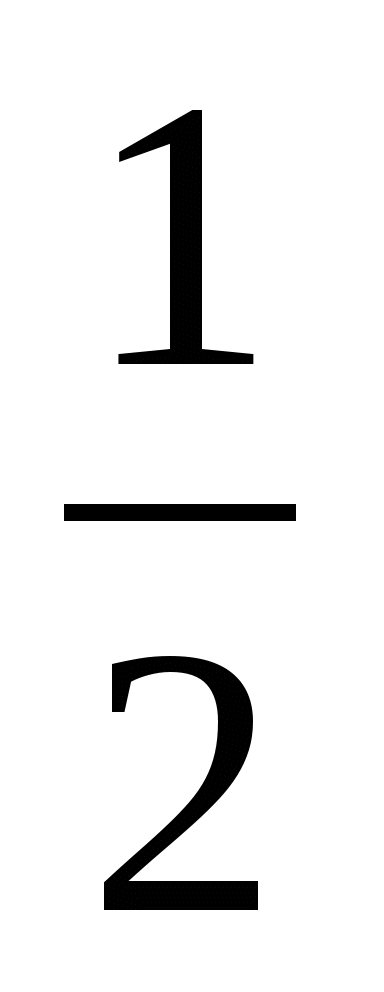Имеем: 1) sin x = 1 ; 2) sin x =

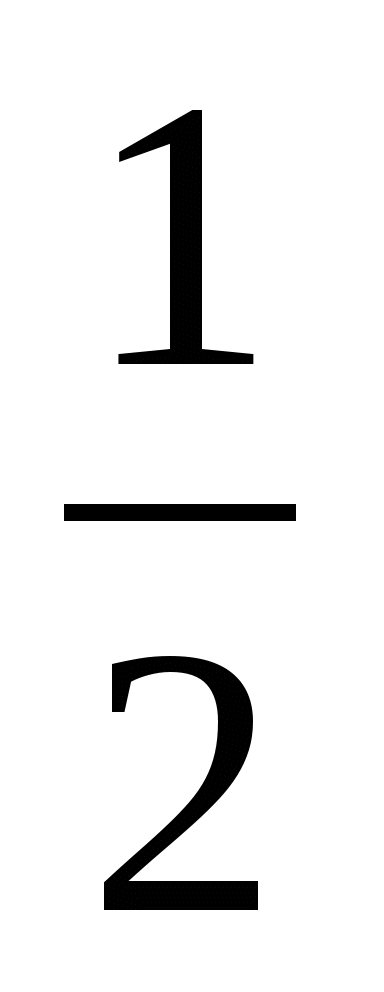
х = 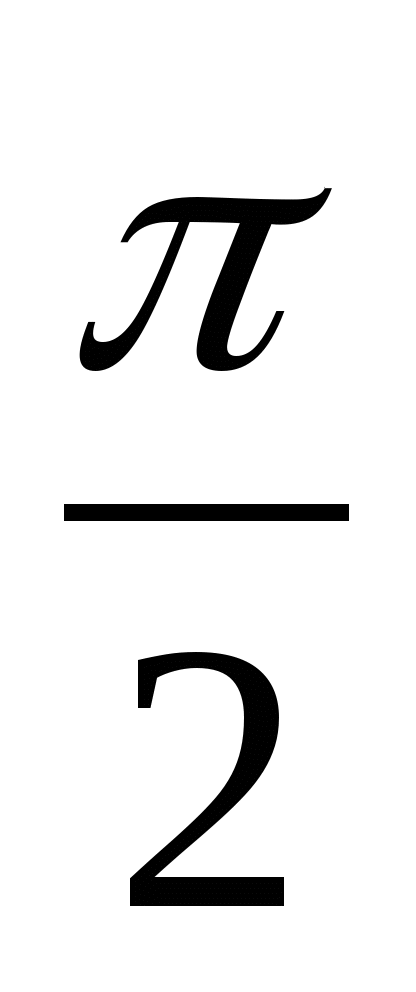+ 2pn , nÎ Z ; х = (-1)^k arcsin 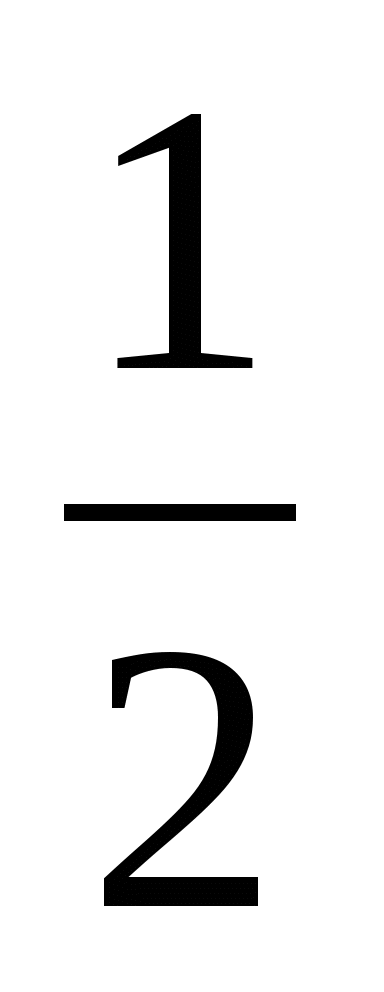+ pk , kÎ Z ;

х = (-1)^k 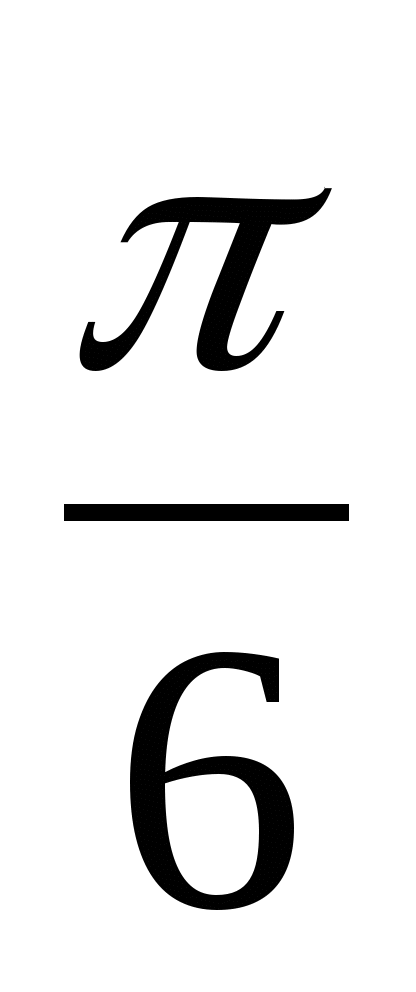+ pk , kÎ Z ;

Ответ : 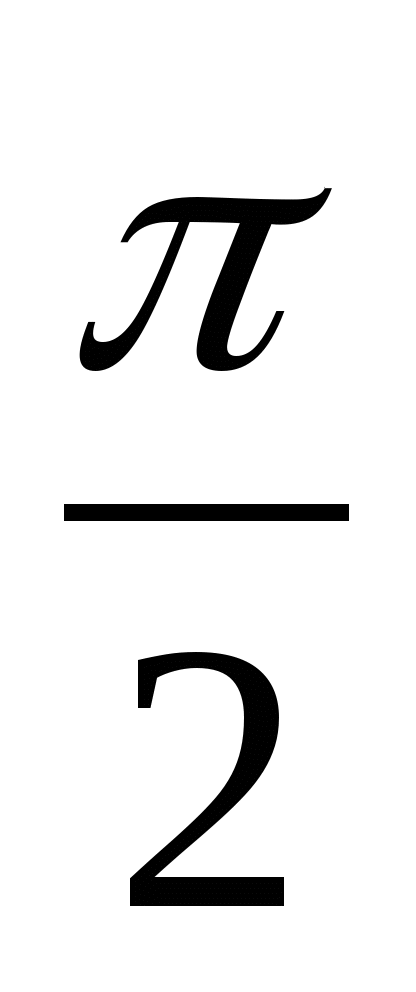+ 2pn , nÎ Z ; (-1)^k 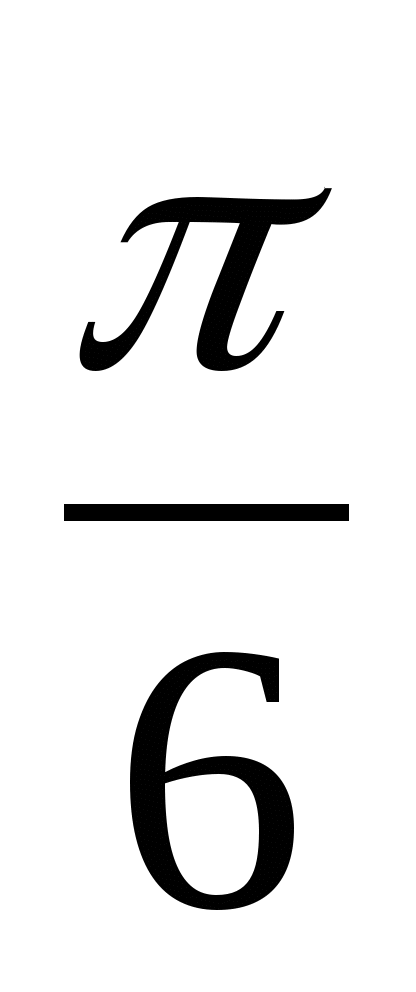+ pk , kÎ Z .

4.Закрепление №11.10 с объяснением у доски.

2 sin ²x + sin x - 1 = 0.

Решение.

Пусть sin x = t , тогда

2t² + t - 1 = 0

t₁ = -1 ; t₂ = .

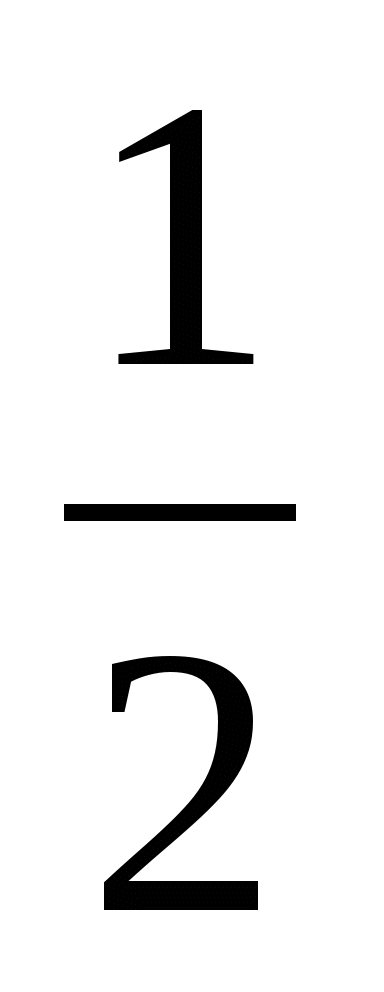Имеем: 1) sin x = - 1; 2) sin x =

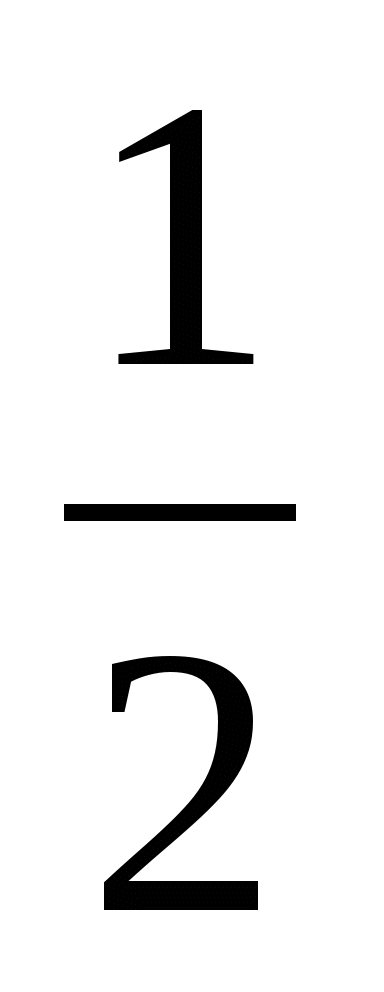
х = - 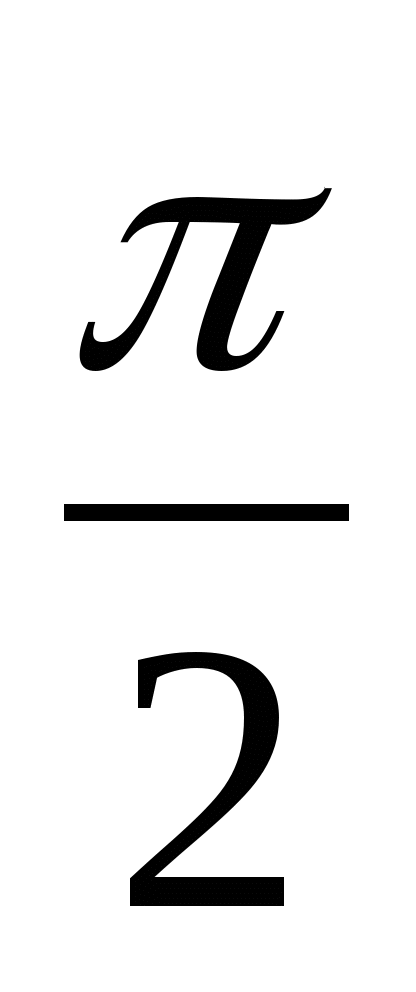+ 2pn , nÎ Z ; х = (-1)^k arcsin 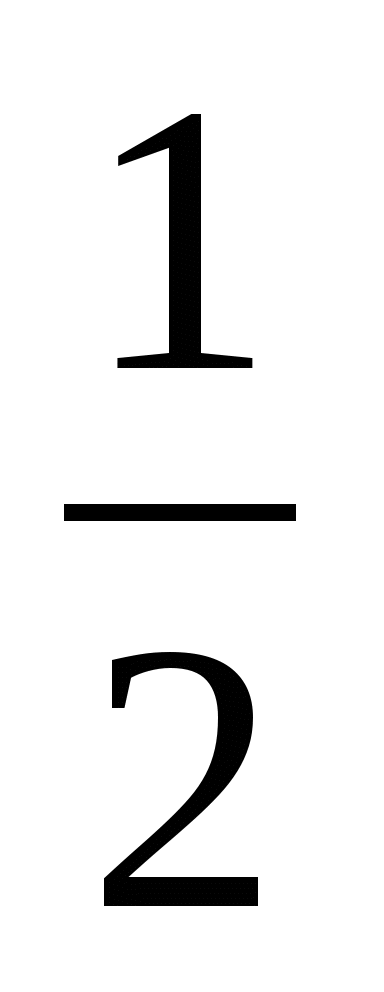+ pk , kÎ Z ;

х = (-1)^k 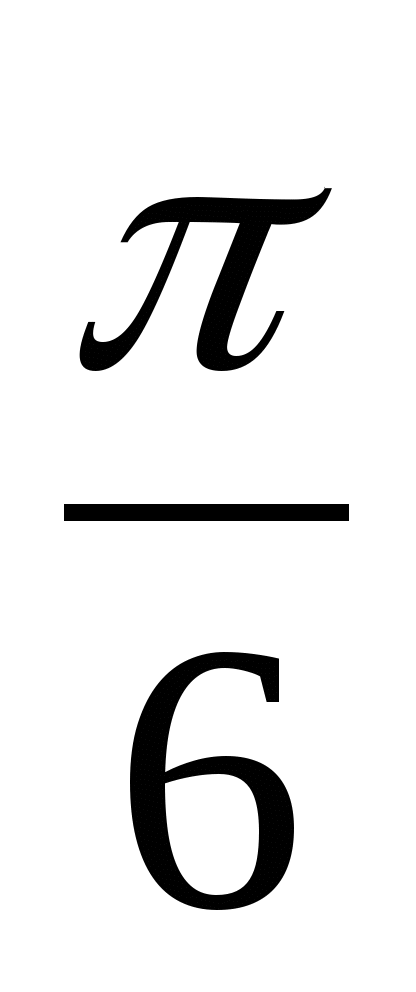+ pk , kÎ Z ;

Ответ: - 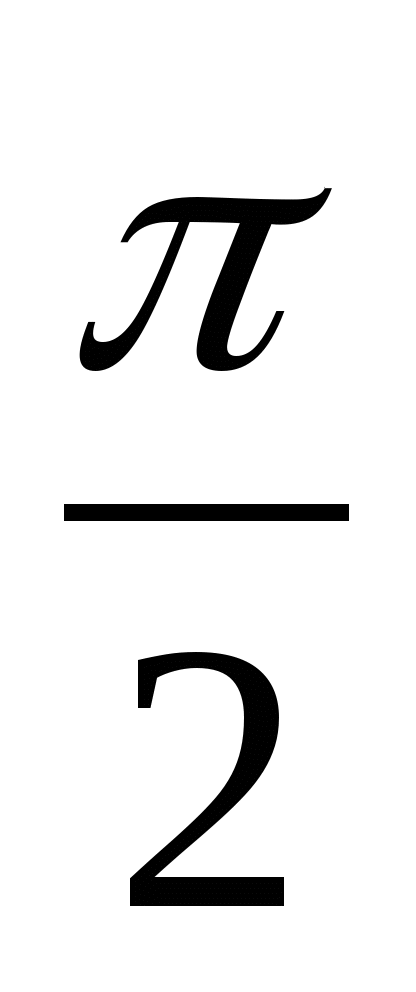+ 2pn , nÎ Z ; (-1)^k 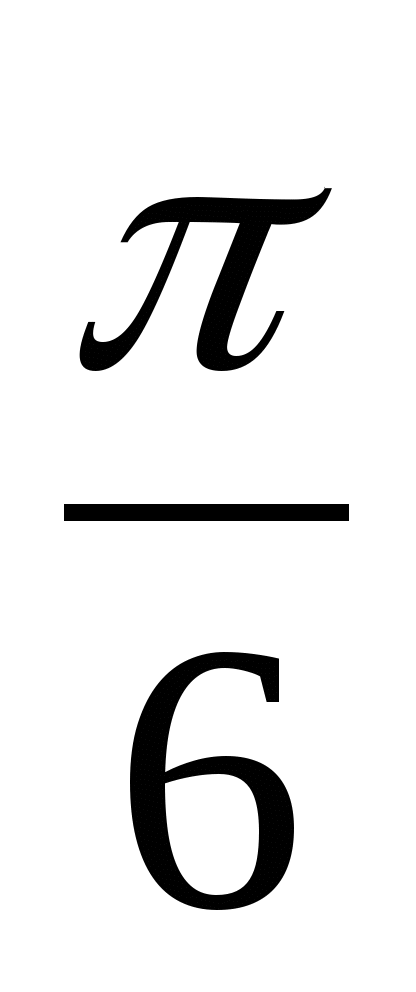+ pk , kÎ Z .

5.Самостоятельно по вариантам решить №11.10 (а, б)

Дома: п 11.2 №11.10(в,д,ж)

Итог урока. Какие уравнения научились решать?

Как решается квадратное уравнение?

Объявить оценки за урок.

Спасибо за работу на уроке.