Учителю
Урок 11 класс. Гауссова кривая. Закон больших чисел.(2 урок. Решение задач)

Урок 11 класс. Гауссова кривая. Закон больших чисел.(2 урок. Решение задач)

Автор публикации: Максютова Э.Х.

Дата публикации: 01.11.2016

Краткое описание:

предварительный просмотр материала

Алгебра и начала анализа

Класс 11а

УМК Мордкович А.Г. (ред.). Алгебра и начала математического анализа. 11 класс. Часть 2. Задачник (профильный уровень)

Уровень обучения профильный

Тема урока: Гауссова кривая. Закон больших чисел. Решения ключевых задач.

Цель:

Образовательная - формирование обобщенных навыков решения задач в теории вероятности и статистике с помощью использования функции Гаусса в приближенных вычислениях; формирование навыков применения закона больших чисел, его применения в реальной жизни; обучение методам приближенного вычисления вероятностей наступления «успехов» в независимых повторениях одного и того же испытания с двумя исходами при большом количестве испытаний; обучение учащихся работе с таблицами приближенных значений для гауссовой функции.

Развивающая- развитие общих приемов мыслительной деятельности; развитие логического мышления.

Воспитательная- воспитание умений, аргументированности, поиск решения в проблемной ситуации.

Задачи:

Образовательные задачи:

- изучить методы решения;

- применить обобщенные знания, умения и навыки в новых условиях.

Развивающие задачи:

- создать содержательные и организационные условия для развития умений решать с помощью функции Гаусса и находить различные способы их решения,

- побуждать учащихся к самоконтролю, взаимоконтролю, самоанализу своей деятельности.

Воспитательные задачи:

- формирование у учащихся познавательного интереса к математике, элементов культуры общения;

- побуждать учащихся к преодолению трудностей в процессе умственной деятельности.

Планируемы результаты:

Учащийся должен знать/уметь

Знать: график, какой функции называется гауссовой кривой; алгоритм использования кривой нормального распределения и функции площади под гауссовой кривой в приближенных вычислениях; закон больших чисел.

Уметь: решать простейшие комбинаторные задачи с использование известных формул;

использовать знания в практической деятельности для анализа числовых данных, представленных в виде диаграмм и графиков; для анализа информации статистического характера.

Техническое обеспечение урока: компьютер, интерактивная доска, презентация, на столе у детей таблица и оценочные листы, анкета.

Содержание урока.

Ход урока.

1.Организационный этап.

Урок 11 класс. Гауссова кривая. Закон больших чисел.(2 урок. Решение задач)

«Математика - царица наук, арифметика - царица математики».

К.Ф. Гаусс.

Учитель ориентирует учеников в работе с оценочными листами.

- Перед вами на партах лежат оценочные листы, в которых вы будете выставлять себе баллы за проделанную работу. Самооценка за урок зависит от суммы набранных баллов на всех этапах. (см. Приложение 1.)

2. Проверка домашнего задания, воспроизведение и коррекция опорных знаний учащихся.

Опрос учащихся: за правильный ответ ученик ставит себе в оценочном листе (1 балл)

Какая функция введена немецким математиком К.- Ф. Гауссом?
Какой формулой задается Гауссова функция?
Какие два замечательных иррациональных числа одновременно присутствуют в формуле?
Где проявляется Гауссова кривая?
Почему данную функцию называют выравнивающей функцией?
Алгоритм использования функции Гаусса в приближенных вычислениях?
Какой ее геометрический смысл и график?
Алгоритм использования функции 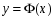в приближенных вычислениях?

3. Постановка целей и задач урока.

Устный счет работа с таблицей.

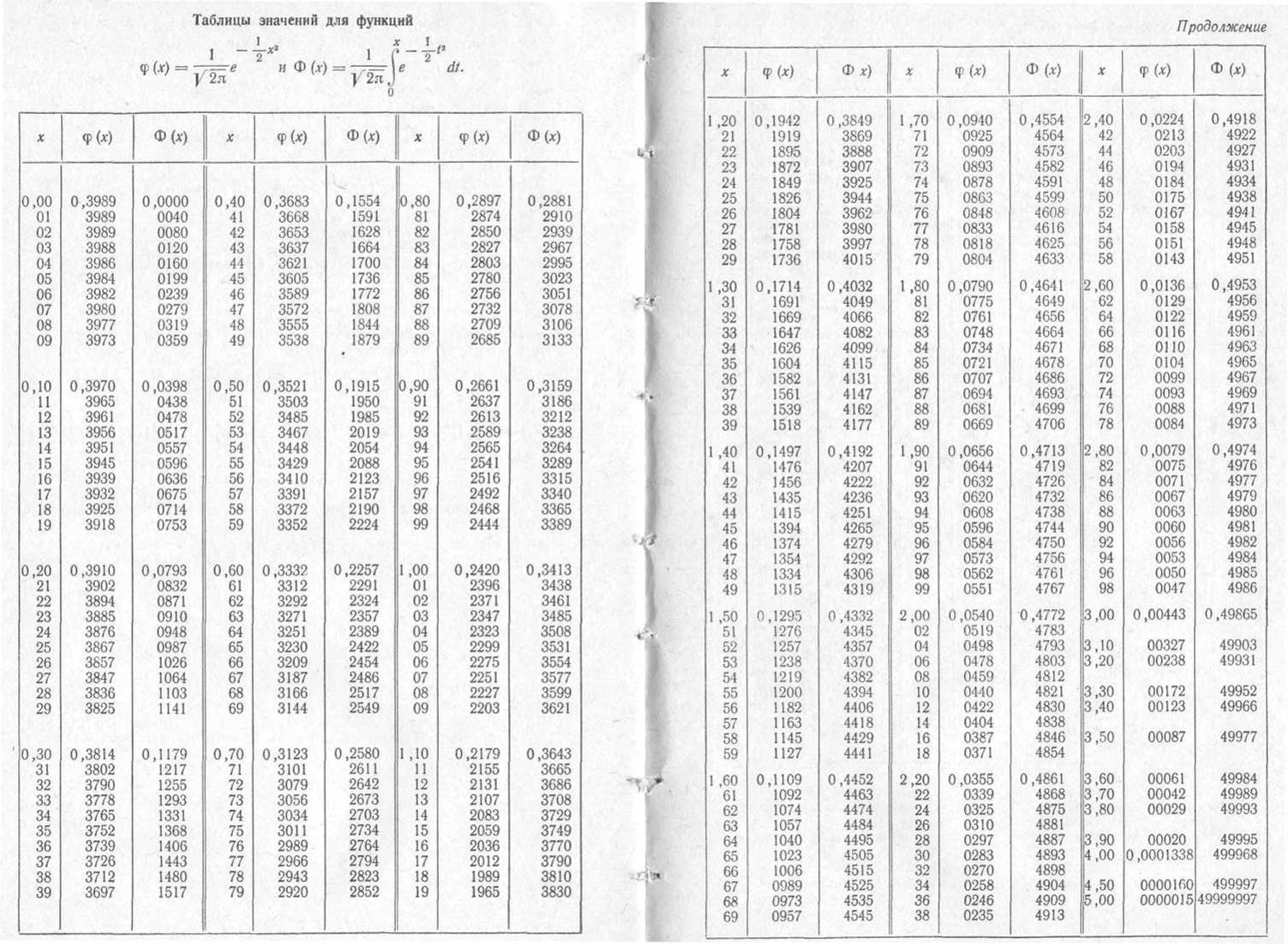
Для использования столь громоздкой формулы гауссовой функции имеются подробные таблицы ее значений. Они составлены для значений аргумента с шагом 0,01. Учащиеся работают с таблицей, выполняют из учебника № 25.7, 25.8, 25.13, 25.14.

За правильные ответы в оценочном листе ученик ставит себе (1 балл)

Ответы:

№25.7 а) 0,242; 0,054; 0,0043 б) 0,3521; 0,1295; 0,0175 в) 0,397; 0,2179; 0,044 г) 0,2661;0,2444; 0,0551
№25.8 1,27; 1,66; 0,03; 2,66
№25.13 0,62; 0,6; 1,66; 2,72
№25.24 1,02; 1,59; 0.01; -2,34

4. Решение задач с помощью алгоритма использования функции Гаусса в приближенных вычислениях и алгоритма использования функции в приближенных вычислениях.

К доске приглашается ученик для рассмотрения способа использования гауссовой кривой для приближенных вычислений в теореме Бернулли.

Задача.

Вероятность рождения мальчика примем равной 50%. Найти вероятность того, что среди 200 новорожденных будет 110 мальчиков.

Решение:

Будем действовать по предложенному алгоритму. В нашем случае п =200, p = q = 0,5. Значит, npq = 50 > 10 и При этом число «успехов» равно 110.

Тогда:

Используя таблицы, вычисляем ответ:

Ответ: 0,02. (за правильное решение ученик получает 5 баллов)

Задача.

Политика П. поддерживает в среднем 40% населения. Какова вероятность того, что из 1500 случайно опрошенных людей политика П. поддерживают от 570 до 630 человек?

Решение.

Считаем, что опрос 1500 человек происходит независимо и что вероятность поддержки политика П. отдельным респондентом, т. е. вероятность «успеха», равна 0,4. Тогда