Контрольная работа Уравнения 10 класс

Возвратные, обобщенные возвратные и симметрические уравнения:

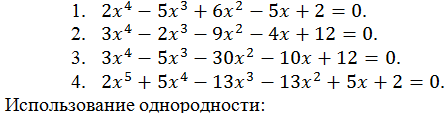
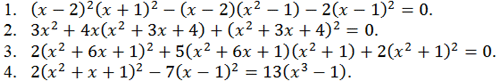
Самостоятельная работа.

Вариант 1.

Решите уравнения

1. Методом группировки x³ - 7x² - 21x + 27 = 0

2. Используя Горнера 4x³ + x² - 5 = 0

3. Методом замены переменной x⁴ + 2x³ - 9x² - 6x + 9 =0

4. Методом замены переменной x(x - 1)(x - 2)(x - 3) = 8

5. Методом замены переменной (2x - 1)²(x + 2)² - (2x - 1)(x² - 4) - 2(x - 2)² = 0

6. Найдите все значения b , при которых один из корней уравнения x³ + 3x² - bx - 8 = 0 равен. Для каждого из найденных значений b определите остальные корни уравнения.

Самостоятельная работа.

Вариант 2.

Решите уравнения.

1. Методом группировки 3x³ - 5x² + 15x - 81 = 0

2. Используя схему Горнера 2x³ - 3x² - 4x + 1 = 0

3. Методом замены переменной x⁴ + 3x³ - 8x² - 12x + 16 = 0

4. Методом замены переменной x(x + 2)(x + 3)(x + 5) = -5

5. Методом замены переменной (2x + 1)⁴ - (2x² + 5x + 2)² - 12(x + 2)⁴ = 0

6. Найдите все значения b, при которых один из корней уравнения равен -2. Для каждого из найденных значений b определите остальные корни уравнения.

Самостоятельная работа.

Вариант 2.

Решите уравнения.

7. Методом группировки 3x³ - 5x² + 15x - 81 = 0

8. Используя схему Горнера 2x³ - 3x² - 4x + 1 = 0

9. Методом замены переменной x⁴ + 3x³ - 8x² - 12x + 16 = 0

10. Методом замены переменной x(x + 2)(x + 3)(x + 5) = -5

11. Методом замены переменной (2x + 1)⁴ - (2x² + 5x + 2)² - 12(x + 2)⁴ = 0

12. Найдите все значения b, при которых один из корней уравнения равен -2. Для каждого из найденных значений b определите остальные корни уравнения.

Контрольная работа 2 10 класс

Вариант 1.

Решите уравнения

1)Методом группировки x³ - 7x² - 21x + 27 = 0

2)Используя схему Горнера 4x³ + x² - 5 = 0

3)Симметрическое x⁴ + 2x³ - 6x² + 2x + 1 =0

4)Методом замены переменной x(x - 1)(x - 2)(x - 3) = 8 5)Однородное 2(x - 1)² - 5(x - 1)(x - 2) + 2(x - 2)² = 0

6)Решите систему уравнений

Х²-3ху+2у²=0

Х²+у²= 20

7. Решить неравенство

(х+8) (х - 5)(х - 3)²

Х+2

Вариант 2.

Решите уравнения.

1. Методом группировки 3x³ - 5x² + 15x - 81 = 0

2. Используя схему Горнера 2x³ - 3x² - 4x + 1 = 0

3. Симметрическое x⁴ - 4x³ +6x² - 4x + 1 = 0

4. Методом замены переменной x(x + 2)(x + 3)(x + 5) = -5

5. Однородное (2x + 1)⁴ - ((2x + 1)(x + 2))² - 12(x + 2)⁴ = 0

6. Решить систему уравнений

2х² - 3ху+ у² =0

У ²- х² =12

7 Решить неравенство

(6-х)²(х+4)

Х+1

Контрольная работа 2 10 класс

Вариант 1.

Решите уравнения

1)Методом группировки x³ - 7x² - 21x + 27 = 0

2)Используя схему Горнера 4x³ + x² - 5 = 0

3)Симметрическое x⁴ + 2x³ - 6x² + 2x + 1 =0

4)Методом замены переменной x(x - 1)(x - 2)(x - 3) = 8 5)Однородное 2(x - 1)² - 5(x - 1)(x - 2) + 2(x - 2)² = 0

6)Решите систему уравнений

Х²-3ху+2у²=0

Х²+у²= 20

8. Решить неравенство

(х+8) (х - 5)(х - 3)²

Х+2

Вариант 2.

Решите уравнения.

7. Методом группировки 3x³ - 5x² + 15x - 81 = 0

8. Используя схему Горнера 2x³ - 3x² - 4x + 1 = 0

9. Симметрическое x⁴ - 4x³ +6x² - 4x + 1 = 0

10. Методом замены переменной x(x + 2)(x + 3)(x + 5) = -5

11. Однородное (2x + 1)⁴ - ((2x + 1)(x + 2))² - 12(x + 2)⁴ = 0

12. Решить систему уравнений

2х² - 3ху+ у² =0

У ²- х² =12

7 Решить неравенство

(6-х)²(х+4)

Х+1