Технологическая карта по алгебре Определение квадратичной функции, построение графика средствами СКМ.

Комментарии: Так как это урок алгебры, то делать полностью урок на изучение построение графика функции средствами СКМ, не вижу смысла, но считаю что данная программа в данном уроке, является неотъемлемой частью. И на уроке не дается полное объяснение и знакомства с средствами СКМ, так как подразумевается, что большинство функций программы были изучены с учениками ранее.

Технологическая карта урока

Ф.И.О. Карташова М.Ш.

Место работы: Муниципальное бюджетное образовательное учреждение «Многопрофильный лицей», г.Муравленко

Должность: учитель математики

Предмет: алгебра

Класс: 8 класс

Базовый учебник: Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. - 12-е изд., испр. и доп. - М.: МнемозинаТема

Определение квадратичной функции. Функции у=ах²+n y=a(x-m)², построение графиков средствами СКМ.

Цель

Научить строить графики функций вида y=ax²+n и y=a(x-m)²

Планируемые результаты

Предметные:

• Знать определение квадратичной функции

• Уметь строить графики функций с помощью преобразований ранее изученных функций, умение определять по графику функцию.

• Научить учащихся строить графики с использованием СКМ

Личностные: развитие самостоятельности и личной ответственности за свои поступки, в том числе в информационной деятельности, на основе представлений о нравственных нормах, социальной справедливости и свободе

Метапредметные: определение общей цели и путей ее достижения; умение договариваться о распределении функций и ролей в совместной деятельности; осуществлять взаимный контроль в совместной деятельности, адекватно оценивать собственное поведение и поведение окружающих;

Основные понятия

Квадратичная функция, квадратные уравнения, коэффициенты уравнения, функция y=ax²

Межпредметные связи

Связь с физикой. астрономией, черчением, с природой.

Ресурсы:

• основные

• дополнительные

презентация, шаблоны параболы, программа Maxima

жетоны для оценивания, линейки, мел, карточки с заданием.

Тип урока

комбинированный

Формы работы учащихся

Г - групповая ( по 2-3 человека)

Необходимое техническое оборудование

Компьютер, интерактивная доска

Дидактическая

структура

урока

Вид работы

Деятельность

учеников

Деятельность

учителя

Планируемые результаты

Предметные

УУД

Организационный момент

1 мин

Деление класс на группы

Китайская пословица гласит:

" Я слушаю - я забываю,

Я вижу- я запоминаю,

Я делаю- я усваиваю.

Ученики готовятся к уроку

Раздает каждому шаблоны параболы.

Программа Maxima включена на компьтерах.

Коммуникативные УУД - Строят план достижения цели, определяют средства.

Регулятивные УУД - Настраиваются на работу, проверяют, все ли приготовили, садятся

Постановка проблемы -3 мин

Применение в природе

Учащиеся рассматривают и определяют чего общего в данных рисунках и знание каких математических понятий нужно .

Учащиеся называют цель урока, делаю вывод о теме урока.

Учитель показывает слайды с применением в природе.

Помогает ученикам сформулировать цель и тему урока.

Умение приводить примеры применения изученной темы на практике и в природе.

Осознание значений математики в повседневной жизни

Ознакомление с целью, этапами урока

Познавательные УУД - Осуществлять актуализацию личного жизненного опыта. Выдвигать гипотезу и обосновывать ее. Коммуникативные УУД - Строить понятные для собеседника высказывания формулировать высказывание, мнение

Регулятивные УУД - Контролируют правильность ответов обучающихся

Актуализация ранее полученных знаний

Время:5 мин

Этапы:

1. Повторение

2. Задание практическое

Повторение изученных тем 7 класса, график функции, свойства, различия

Функция у=ах², ее график и свойства.

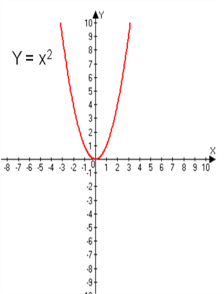
График квадратичной функции носит название парабола

АПОЛЛОНИЙ ПЕРГСКИЙ (расцвет деятельности - вторая половина 2 в. до н.э.), древнегреческий математик родом из Перги в Памфилии, прозванный современниками Великим геометром. Занимался математикой в Александрии под руководством учеников Эвклида.

Аполлоний ввел понятия параболы и дал ее теорию, сохранившуюся в практически неизменном виде до эпохи Ньютона.

На слайдах, также показаны сравнения различных функций вида у=ах²

Установите соответствие

Отвечают на вопросы учителя, если что-то считают нужным, то конспектируют

Ученики устанавливают соответствие.

Учитель задает соответственно вопросы, кто быстрее поднимает руку и правильно говорит ответ, тот ученик получает жетон.

Напоминает основные понятия 7 класс

Учитель дает задание на правильное соответствие функции и графика

Знание основных определений по теме

Строить графики элементарных функций: исследовать свойства числовых функций на основе изучения поведения их графиков.

Знание исторического материала

Познавательные УУД - Доказывать, аргументировать свою точку зрения

Коммуникативные УУД - -извлечение из текстов необходимой информации;

Регулятивные УУД - По мере необходимости исправляют, дополняют, уточняют выступления.

Изучение нового материала

Этапы:

1. </<font face="Times New Roman, serif">СКМ

Основные понятия и обозначения, необходимые для построения графика квадратичной функции.

Перед изучением данного пункта, учитель задает вопросы о СКМ, а именно основных функциях программы Maxima, с которыми ребята уже познакомились.

Функция: plot2d - построение двумерных графиков

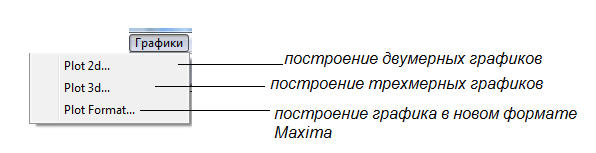
Открываем программу, пишем в текстовом формате Построение графика квадратичной функции.

Начинаем ввод формул. Данных функций и проверяем правильно ли выполнили задание.

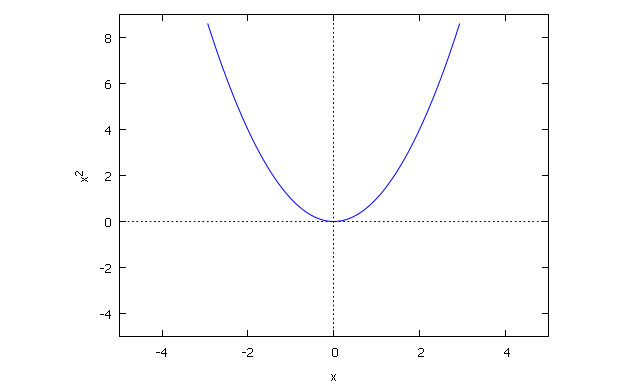
Смотрим данный график это парабола y=x²

Под руководством учителя, строят графики и выполняют проверку своего соответствия

После установки соответствия, учитель предлагает учащимся познакомиться с элементами построения графика в программе Maxima

Актуализация ранее полученных знаний

Изучение новой функции программы Maxima.

Умение строить графики, использую полученные знания.

Познавательные УУД - умение искать и выделять главное в полученной информации.

Коммуникативные - умение отстаивать свою точку зрения.

Регулятивные УУД- по мере необходимости исправляют, дополняют, уточняют выступления.

2. Опр-ние

3. у= ax² + n

4.у=a(х-m)²

• Определение: Квадратичной функцией называется функция вида у=ах²+bx+c, где a, b, c - любые действительные числа, а≠0, х- независимая переменная.

• Область определения: множество всех действительных чисел R

Некоторые виды квадратичной функции у=ах²+n y=a(x-m)²

Построим у=х²+2 с помощью программы, и сравним с первоначальным графиком.

Скажите что вы заметили? Сделайте вывод.

• График функции у=ах²+n есть парабола, полученная из графика функции у=ах² в результате сдвига вдоль оси ординат вверх на n единиц при n>0 или вниз на n единиц при │n│<0

у= ax² + n

а > 0 а < 0

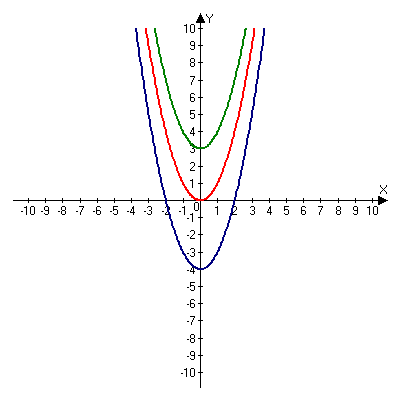
у = x² у = x² - 4 у = x² + 3

у=a(х-m)²

Постройте самостоятельно у=(х-3)² (для построения лучше взять точки от -1 до 4 примерно)

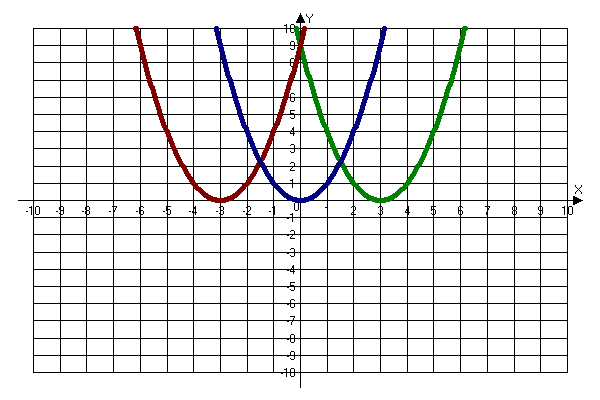
График функции у=а(х-m)²+n есть парабола, полученная из графика функции у=ах² в результате сдвига вправо вдоль оси абцисс на m единиц при m>0 или влево на m единиц при │m│<0

а > 0 а < 0

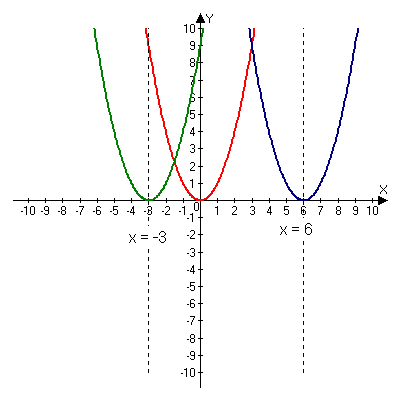
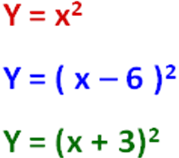
Ученики выполняют задание учителя, построение графиков, записывают новые определения, свойства и правила построения функций

Делают вывод, о том если ветви направлены вверх, то а- положительное, если вниз, то а - отрицательное.

В программе выполняют построение, делают выводы.

Под руководством учителя, но и самостоятельно строят графики, делаю совместные выводы.

Данные графики строят самостоятельно

Учитель на примерах начинает объяснять тему, предлагает учащимся провести сравнение двух графиков и вывести правило, как получили график данного вида.

Вывод могут написать в комментариях в программе, а само правило в тетради.

Учитель контролирует выполнение работ, если не получается, объясняет дополнительно

Учитель напоминает, как именно нужно писать комментарии или текст в программе.

Владение базовым понятийным аппаратом, необходимым для получения дальнейшим образованиям.

Закрепление навыка работы с графиками методами СКМ.

Познавательные УУД - Групповое - обсуждение и выведение правил.

Коммуникативные УУД - построение логической цепи рассуждений, доказательство.

Регулятивные УУД - В ходе заслушивания выступления группы остальные школьники контролируют правильность и понятность ответов.

Закрепление нового материала

Время: 5 мин

Этапы:

Установите соотвествие:

у = х² - 5

у = 0,3х²

у = - (х - 3)²

у = - (х+ 2)² +5

Ответ: 1 - синий, 2 - красный, 3 - жёлтый, 4 - зеленый

Ученики выполняют задание устно, желающие могут быстро проверить на компьютере.

Под заданием пишут ответ .

Учитель дает задание, где нужно найти соответствие графика и функции.

Научиться строить график функции путем преобразования известных графиков.

Познавательные УУД - осуществлять переработку математической информации для ее дальнейшего использования;

Коммуникативные УУД - Обсуждают и анализируют полученные результаты.

Регулятивные УУД - В ходе заслушивания выступления группы остальные школьники контролируют правильность и понятность ответов.

Рефлексия

Время: 2 мин

Этапы:

Можно ответить на любой из вопросов или закончить фразу:

1. Наш урок подошёл к концу, и я хочу сказать…

2. Для меня было открытием то, что…

3. За что ты можешь себя похвалить?

4. Что на ваш взгляд не удалось? Почему?

5. Что учесть на будущее?

6. Мои достижения на уроке.

Подсчет жетонов каждой группы. Сообщение оценок за урок.

Ученики произвольно выбирают вопрос или фразу, заканчивая ее.

С группы отвечает один человек, если остается время то можно тем кто еще желает высказаться.

Подводит итоги урока, предлагая учащимся ответить на вопросы.

Регулятивные УУД - Оценка результатов работы

Коммуникативные УУД - Слушать собеседник, строить понятные для собеседника высказывания