Урок + презентация по математике (геометрия) для 7 класса по теме «Сумма углов треугольника»

Тема урока: Сумма углов треугольника

Цели:

образовательная - сформулировать и доказать теорему о сумме углов треугольника; рассмотреть применение теоремы при решении задач;

развивающая - развитие абстрактного мышления, навыков исследовательской деятельности; устной и письменной математической речи;

воспитательная - воспитание нравственных качеств личности, аккуратности, формирование интереса к изучению геометрии.

Тип урока: урок изучения нового материала

Метод обучения: объяснительно-иллюстративный, эвристический

Требование к знаниям, умениям и навыкам учащихся:

учащиеся должны знать формулировку теоремы о сумме углов треугольника и ее доказательство; уметь применять теорему при решении задач.

Оборудование: линейка, проектор, экран, презентация, модели треугольников и ножницы (для каждого ученика)

Литература:

1. Геометрия : учебник для 7-9 кл. сред. шк. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. - М. : Просвещение, 2008.

2. Гаврилова Н. Ф. Поурочные разработки по геометрии. 8 класс. - М. : ВАКО, 2004.

3. Глейзер Г. И. История математики в школе. - М. : Просвещение, 1964.

План урока:

1. Оргмомент

2. Актуализация знаний

3. Выполнение исследовательской работы

4. Доказательство теоремы

5. Физкультминутка

6. Закрепление изученного материала

7. Самостоятельная работа

8. Домашнее задание

9. Подведение итогов

Ход урока:

I. Оргмомент

(слайд 1)

Учитель:

Посмотрите, всё в порядке -

Книжки, ручки, тетрадки?

Прозвенел звонок, начинаем наш урок!

Запишите в тетрадях сегодняшнее число, классная работа.

II. Актуализация знаний, умений, навыков

(слайд 2)

Учитель: В учебнике геометрии Игоря Фёдоровича Шарыгина можно найти такие слова: «Высшее проявление души - это разум; высшее проявление разума - это геометрия. Клеткой геометрии, основным ее понятием, является некоторая геометрическая фигура. По его мнению, свойства этой фигуры так же неисчерпаемы, как и Вселенная». Как вы думаете, о какой геометрической фигуре идет речь?

Ученики: Треугольник.

(слайд 3)

Учитель: Совершенно верно, речь идет о треугольнике. Треугольник в геометрии играет особую роль. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о геометрии треугольника, как самостоятельном разделе геометрии.

Давайте вспомним, что мы знаем о треугольнике?

(слайд 4)

Ученики: Треугольник - это геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки.

Учитель: Какие бывают треугольники?

Ученики: Разносторонние, равносторонние, равнобедренные.

Учитель: Сформулируйте свойства равнобедренного треугольника.

Ученики: В равнобедренном треугольнике углы при основании равны; а также биссектриса, проведенная к основанию является медианой и высотой.

(слайд 5)

Учитель: Нами изучены признаки равенства треугольников. Сколько признаков равенства треугольников вы знаете?

(слайд 6)

Учитель: Назовите основные элементы треугольника?

Что называется медианой, биссектрисой, высотой треугольника?

Ученики: Медиана треугольника - отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

(слайд 7)

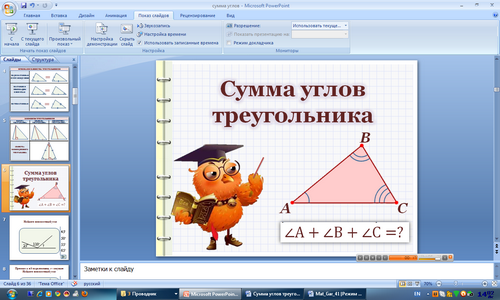
Учитель: Сегодня на уроке мы изучим еще одно важное свойство треугольника - рассмотрим теорему о сумме его треугольника.

Запишите в тетрадях тему урока «Сумма углов треугольника».

Учитель: Начнем урок с небольшой геометрической разминки - решим несколько задач на готовых чертежах.

Задачи на готовых чертежах.

(слайды 8 - 12)

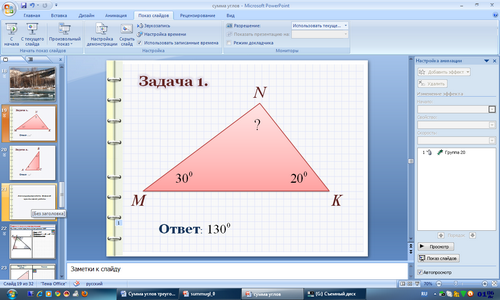
Задача 1.

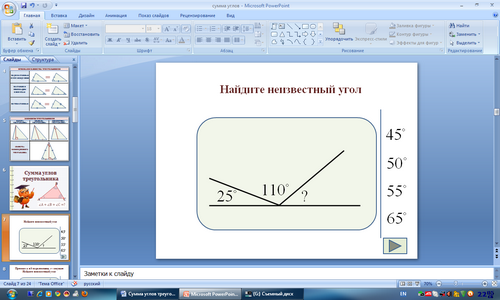Ответ: 45⁰

Задача 2.

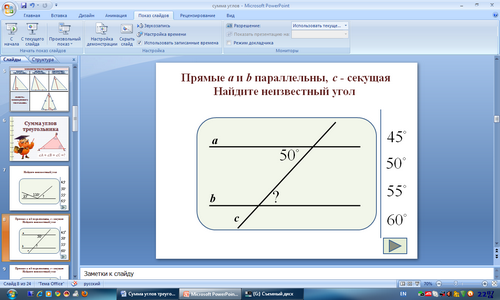Ответ: 50⁰

Задача 3.

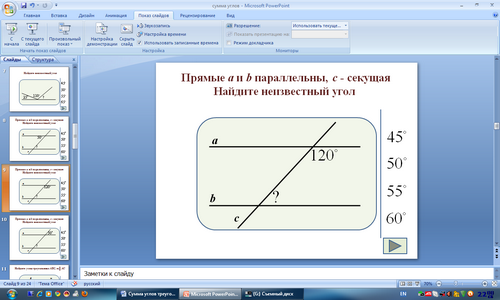Ответ: 60⁰

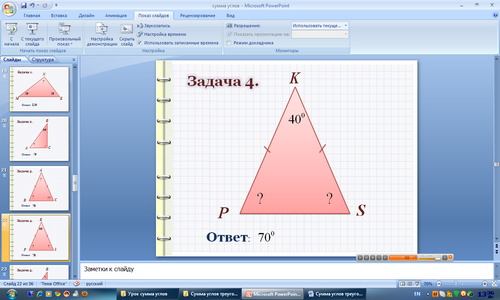
Задача 4.

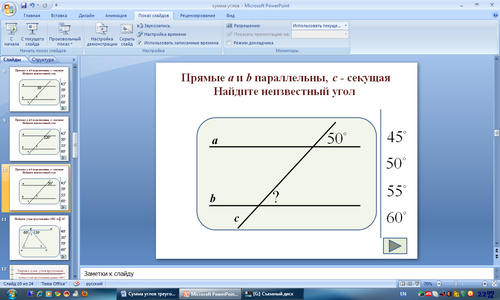Ответ: 50⁰

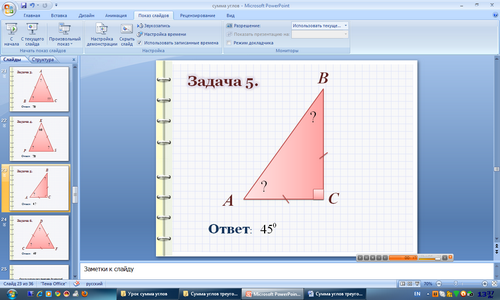
Задача 5.

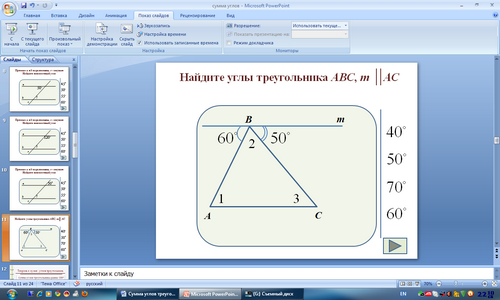Ответ: 60⁰, 70⁰, 50⁰

Учитель: В последней задаче получили, что сумма углов треугольника равна 180⁰. Случайно ли, это? А чему равна сумма углов этого треугольника (показывает модель), или этого? Также 180⁰? Или все-таки равняется другому числу? Это нам пока неизвестно и только лишь предстоит узнать.

III. Выполнение исследовательской работы

Ребята! Очень часто ученые устанавливают важные факты экспериментальным путем. Это происходит в разных областях науки: в физике, химии, математики. Я вам тоже сегодня предлагаю побыть в роли исследователей. Выполним небольшую исследовательскую работу. Работаем в парах. На столах у каждого из вас лежат треугольники. Сейчас с помощью эксперимента установим, чему равна сумма углов треугольника.

(слайд 13)

План исследования:

1. Отрежьте ножницами углы треугольника

2. Соберите их в одной точке.

3. Ответьте на вопросы: какой угол образовали углы треугольника? Чему равна его градусная мера?

4. Сделайте вывод.

Учитель: Таким образом, мы экспериментальным путем установили, что сумма углов треугольника равна 180⁰. Можем ли мы это утверждение считать истинным для любого треугольника?

Ученик: Нет, это всего лишь предположение. В геометрии истинность утверждений устанавливается путем логических рассуждений, опирающихся на аксиомы и ранее изученные теоремы.

IV. Доказательство теоремы

(слайд 14)

Учитель: Итак, нам необходимо доказать теорему:

Сумма углов треугольника равна 180⁰.

Изобразим в тетрадях произвольный треугольник АВС.

Учитель: Ребята, из каких частей состоит любая теорема?

Ученики: Теорема состоит из условия и заключения.

Учитель: Что в данной теореме является условием (что дано)?

Ученики: Дан треугольник.

Учитель: Сформулируйте заключение теоремы (что нужно доказать).

Ученики: Необходимо доказать, что сумма углов треугольника равна 180⁰.

(Делаем рисунок и запись на доске)

Учитель: Посмотрите внимательно на заключение теоремы. Нам необходимо доказать, что сумма углов треугольника равна 180⁰. А в каких ранее изученных фактах, мы сталкиваемся с числом 180?

Ученики: 1) развернутый угол равен 180⁰; 2) сумма смежных углов равна 180⁰; 3) если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180⁰.

Учитель: Так как смежные углы в сумме образуют развернутый угол, то предлагаю 1) и 2) варианты рассматривать как один факт. Развернутый угол равен 180⁰. Как же можно доказать теорему?

(слайд 15)

Учитель: Я предлагаю еще раз вернуться к задаче, решенной нами в начале урока. Она нам поможет найти способ доказательства теоремы. В задаче нам была дана прямая, параллельная одной из сторон треугольника, путем составления пар равных накрест лежащих углов мы нашли углы треугольника, и тем самым увидели, что их сумма равна 180⁰.

Учитель: Чтобы доказать теорему я предлагаю вам выполнить дополнительные построения. Проведем через вершину В прямую а, параллельную стороне АС. Введем обозначения получившихся углов. Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ. Углы 3 и 5 - накрест лежащие углы при пересечении тех же параллельных прямых секущей ВС. Поэтому 4 = 1, 5 = 3. Сумма углов 4, 2, 5 равна развернутому углу с вершинойВ, т. е. 4 + 2 + 5 = 180⁰. Отсюда, учитывая равенства , получаем, 1 + 2 + 3 = 180⁰ илиА + В + С =180⁰.

Запишем доказательство теоремы в тетрадь:

1. Проведем через вершину В прямую аАС.

2. 4; 3=5 (как накрест лежащие).

3. 2 + 5 = (т.к. образуют развернутый угол с вершиной В).

4. Из (2) =>1 + 2 + 3 = 180⁰ илиА + В + С =180⁰.

(слайд 16)

Учитель: Подтвердилось наше предположение? Еще раз сделаем вывод о сумме углов треугольника.

Ученики: Сумма углов треугольника равна 180⁰

(слайд 17)

Учитель: Ни на миг не прерывается связь между поколениями, ежедневно мы усваиваем опыт, накопленный нашими предками. Такое доказательство теоремы о сумме углов треугольника было открыто Пифагором еще в (V в. до н.э.). А вот Евклид в своих «Началах» излагает другое доказательство теоремы о сумме углов треугольника, основанное на свойстве односторонних улов при пересечении двух параллельных прямых секущей. Рассмотрим этот способ.

(слайд 18)

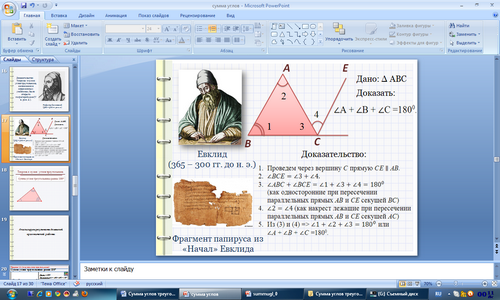
Доказательство:

1. Проведем через вершину С прямую СЕ АВ.

2. 

3. (как односторонние при пересечении параллельных прямых АВ и СЕ секущей ВС)

4. (как накрест лежащие при пересечении параллельных прямых АВ и СЕ секущей АС)

5. Из (3) и (4) => или А + В + С =180⁰.

Учитель: Итак, мы доказали одну из важнейших теорем геометрии - теорему о сумме углов треугольника. Теперь предлагаю вам немного отдохнуть.

(на фоне музыки)

V. Физкультминутка

(слайд 19)

Встаньте, поднимите руки вверх, потянитесь к звездам; покажите развернутый угол; прямой угол; тупой угол; острый угол.

Молодцы! Садитесь!

VI. Закрепление изученного материала.

Учитель:

Решение задач на готовых чертежах

(слайды 20 - 25)

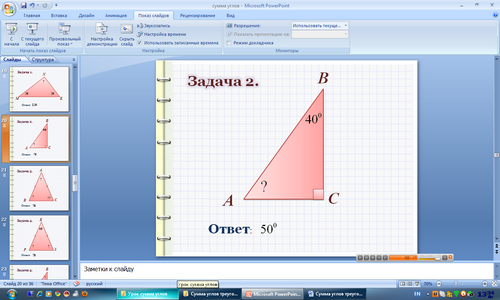
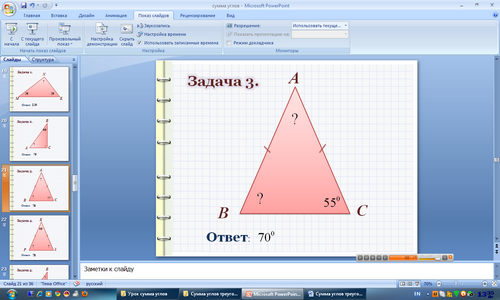
(слайд 26)

Решение задачи из учебника № 224 стр. 71

Решение:

1. Пусть одна часть xº. Тогда А = 2 x º , В = 3 xº, С = 4 xº .

2. А +В +С=180º (по теореме о сумме углов треугольника) =>

3. 2х + 3х + 4х = 180⁰,

х = 20

А=40º, В=60º, С=80º.

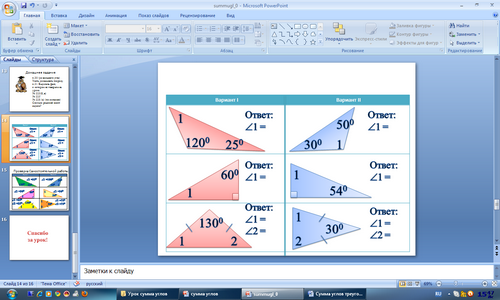
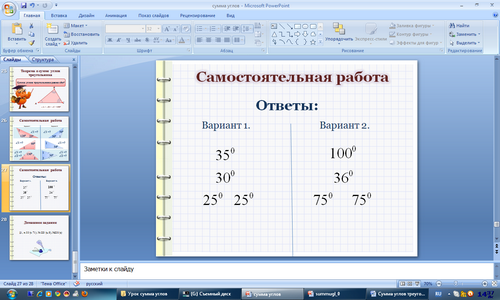
VII. Самостоятельная работа. (слайд 27)

(слайд 28)

(слайд 29)

VIII. Домашнее задание: §1, п. 33 (с. 71); № 223 (а, б), № 228 (а)

(слайд 30)

IX. Подведение итогов

Что нового вы узнали сегодня на уроке?

Сегодня на уроке мы доказали одну из важнейших теорем геометрии - теорему о сумме углов треугольника, рассмотрели два способа ее доказательства, и решение задач на применение теоремы.

Мы не открыли что-то новое в геометрии, но каждый сделал открытие для себя. К тайнам извечный разум влекущий, путь бесконечный осилит идущий (Т. Малевич).