- Учителю
- План-конспект урока ' Решение ключевых задач по теме Пирамида' 10 класс
План-конспект урока ' Решение ключевых задач по теме Пирамида' 10 класс
План-конспект урока
«Решение ключевых задач по теме ПИРАМИДА»
10 класс
Учитель математики
Мыкалова Наталья Евгеньевна
МБОУ средняя школа №2
г.Лысково
Нижегородской области
2014 год
Цель:
Образовательная - формирование обобщенных навыков приемов решения задач; формирование навыков построения высоты пирамиды; рассмотрение случаев расположения проекции вершин неправильной пирамиды.
Развивающая - развитие пространственного воображения, развитие общих приемов мыслительной деятельности; развитие логического мышления.
Воспитательная - воспитание аккуратности при выполнении чертежей, воспитание конструктивных умений, аргументированности, поиск решения в проблемной ситуации.
Задачи: систематизировать знания по теме «Пирамида»,
закрепить навыки построения пирамид,
изучить случаи различного расположения проекции вершины в неправильной пирамиде.
УМК: «Геометрия 10» Л.С. Атанасян, В.Ф. Бутузов
Тип урока: комбинированный - содержательно-поисковый
Методы: по познавательной деятельности -
проблемной подачи материала, эвристический (частично-поисковый);
методы, характеризующие мыслительные операции при подаче и усвоению учебного материала -
индуктивный, дедуктивный, синтеза и анализа, сравнения, обобщения, систематизации,
системного анализа, сравнительный, гипотез;
методы, обеспечивающие передачу учебной информации - практические, иллюстративно-объяснительный;
методы контроля - фронтальные, групповые, индивидуальные, письменные самопроверки.
Формы работы: групповая, индивидуальная.
Оборудование: модели призм и пирамид, плакаты, карточки для индивидуальной работы, проектор.
План урока: 1) Организационный момент
2) Актуализация опорных знаний, создание проблемной ситуации
3) Этап подачи нового материала: рассмотрение случаев расположения проекции вершины неправильной пирамиды
4) Этап усвоения материала и формирование умений и навыков: решение задач
5) Контроль и рефлексия.
Ход урока
І. Организационный момент: объявление темы и целей урока. (2мин.)
«Решение ключевых задач по теме ПИРАМИДА» (слайд 1)
ІІ. Актуализация опорных знаний. (12мин.)
-
У доски с индивидуальными заданиями(2 человека).
-
Индивидуальные карточки (8 человек)
-
Фронтальный опрос (остальные) (слайд 2)
Фронтальный опрос
-
Определение призмы
-
Определение многогранника
-
Виды призм
-
Определение пирамиды
-
Виды пирамид
Проверка выполнения задания у доски с комментариями.
ІІІ. Этап подачи нового материала. (15 мин.)
Эвристическая беседа, схема-таблица, презентация, поиск ответа на проблемный вопрос.
-
- Дополнительные вопросы к Заданию у доски №2 (слайд 3)
Вид ∆ ABS. (прямоугольный по теореме обратной теореме Пифагора)
Найти высоту пирамиды.
Для того чтобы ответить на этот вопрос, необходимо найти проекцию вершины пирамиды. Чем мы сегодня и займёмся (слайд 4)
Учащимся раздаётся таблица-схема.
Случай 1. Учитель доказывает у доски (слайд 5)
Случай 2-3. Вывод из предыдущего случая в ходе эвристической беседы, доказательство самостоятельно в домашней работе (слайд 6-7)
Случай 4. Условие ставиться учителем, доказательство выполняет ученик (слайд 8)
Случай 5-6. Вывод из случая 4 в ходе эвристической беседы, доказательство самостоятельно в домашней работе (слайд 9-10)
Случай 7. Условие ставиться учителем, доказательство выполняют в парах (слайд 11)
В результате работы появляется заполненная таблица.
Если в пирамиде
то основание высоты лежит на (в)
Доказательство
Два боковых ребра равны
(все боковые ребра равны)
Серединном перпендикуляре к общему ребру основания
(в центре описанной окружности)
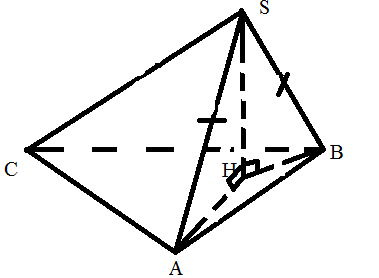 SA =SB, значит
SA =SB, значит
∆ASH = ∆BSH(по катету и гипотенузе), значит
AH = BH, значит
H лежит на серединном перпендикуляре к ребру АВ.
Два боковых ребра равнонаклонены к плоскости основания
(все боковые ребра равнонаклонены к плоскости основания)
Серединном перпендикуляре к общему ребру основания
(в центре описанной окружности)
∟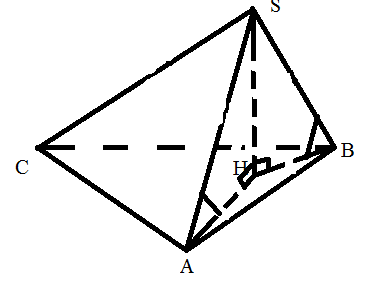 SAH =∟SBH, значит ∆ASH = ∆BSH(по катету и острому углу), значит
SAH =∟SBH, значит ∆ASH = ∆BSH(по катету и острому углу), значит
AH = BH,отсюда
H лежит на серединном перпендикуляре к ребру АВ.
Два боковых ребра составляют с высотой пирамиды равные углы
(все боковые ребра составляют с высотой пирамиды равные углы)
Серединном перпендикуляре к общему ребру основания
(в центре описанной окружности)
∟АSH =∟ВSH
значит ∆ASH = ∆BSH(по катету и острому углу), значит
AH = BH,отсюда
H лежит на серединном перпендикуляре к ребру АВ.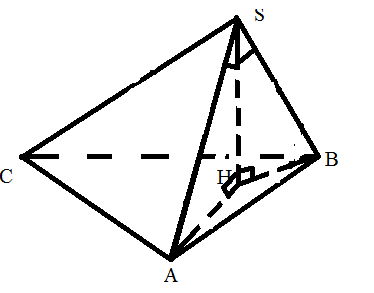
Две высоты боковых грани равны
(все высоты боковых граней равны)
Биссектрисе общего угла основания
(в центре вписанной окружности)
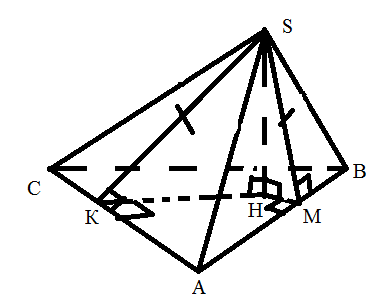 SK = SM,
SK = SM,
значит ∆SKH = ∆SMH(по катету и гипотенузе),
отсюда KH = MH, HK ┴AB, HM┴ BC,
значит Н лежит на биссектрисе ∟А
Два двугранных угла при основании равны
(все двугранные углы при основании равны)
Биссектрисе общего угла основания
(в центре вписанной окружности)
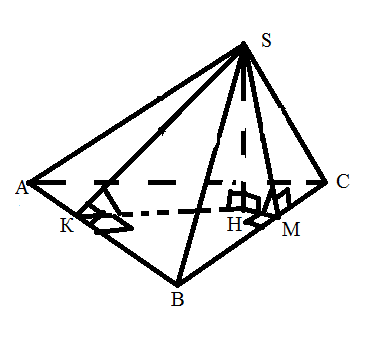 Двугранные углы SABH и SBCA равны, значит ∟SMH =∟SKH(линейные по построению), отсюда ∆SMH = ∆SKH (по катету и гипотенузе), значит MH = HK, отсюда Н лежит на биссектрисе ∟А
Двугранные углы SABH и SBCA равны, значит ∟SMH =∟SKH(линейные по построению), отсюда ∆SMH = ∆SKH (по катету и гипотенузе), значит MH = HK, отсюда Н лежит на биссектрисе ∟А
Боковое ребро составляет равные углы с ребрами основания
(все боковые ребра составляют равные углы с ребрами основания)
Биссектрисе общего угла основания
(в центре вписанной окружности)
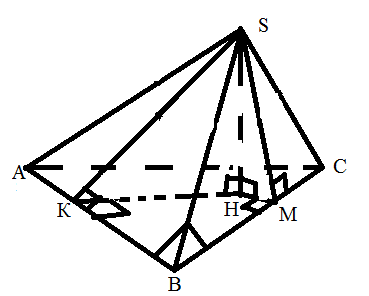 ∟SBA = ∟SBC,
∟SBA = ∟SBC,
значит ∆SKB = ∆SMB(по катету и гипотенузе),
отсюда SK = SM,
получаем случай 4.
Боковая грань перпендикулярна основанию
Высота пирамиды - высота этой боковой грани
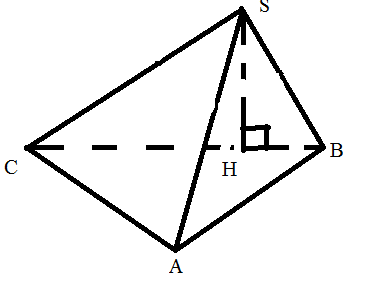 BSC┴ABC,значит SH┴ABC
BSC┴ABC,значит SH┴ABC
ІV. Этап усвоения материала и формирование умений и навыков. (10 мин.)
-
Самостоятельное решение задачи №2 (слайд 12)
Задание №2
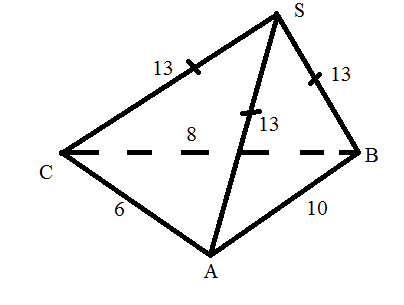
Найти высоту пирамиды
Решение:
SA = SB = SC, значит H -центр описанной окружности ∆ ABС;
∆ ABС - прямоугольный, значит Н - середина гипотенузы АВ;
По теореме Пифагора для ∆ AНS SH = 12 см.
Ответ: высота SH = 12 см
V. Контроль и рефлексия. (2мин.)
-
Учащиеся заполняют анкету (слайд 13)
Тема сегодняшнего урока:
Главный объект урока:
Главный вопрос урока:
Оценка, которую я ставлю себе за понимание темы
Для успешного решения задач по этой теме мне надо повторить
1)
2)
3)
Домашнее задание: 1) доказать оставшиеся случаи.
2) в задачах №245, 246, 249, 250 сделать чертежи.
Дидактический материал
Задание у доски №1
Построить правильную шестиугольную пирамиду
Задание у доски №2
Сделать выносные чертежи 
1) ∆ ABS
2) ∆ABC
Индивидуальные задания
-
Карточка №1
Построить правильную четырехугольную пирамиду
Перечислить её элементы
-
Карточка №2
Построить правильную треугольную пирамиду
Перечислить её элементы
-
Карточка №3
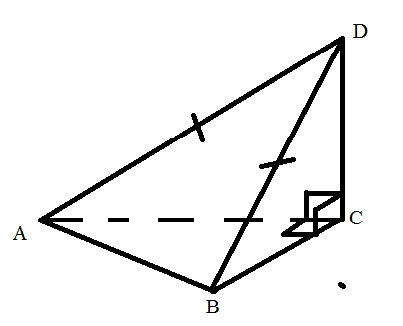
Сделать выносные чертежи
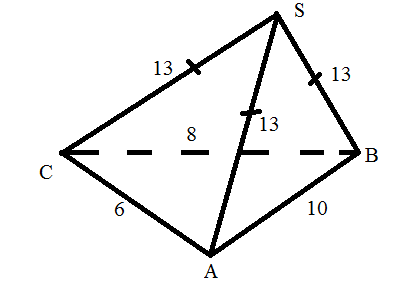
1) ∆ СBS
2) ∆SDB
3) ABCD
-
Карточка №4
Сделать выносные чертежи
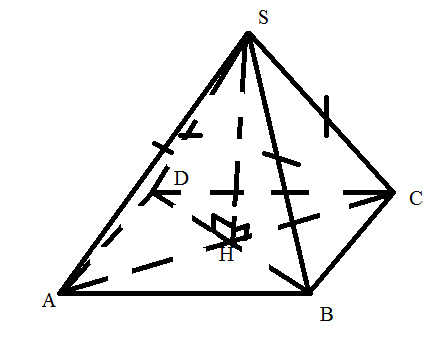
1) ∆ ABD
2) ∆ABC
3) ∆BCD
Если в пирамиде
то основание высоты лежит на(в)
Доказательство