Урок игра в 5 классе

Математическое состязание «Умницы и умники».

Акмеологическое внеклассное занятие по математике в 5 классе.

Цель:

1. Систематизировать и обобщить знания учащихся по теме «Обыкновенные дроби»: понятие дроби, виды обыкновенных дробей, сравнение дробей, связь дробей и действия деления, смешанные числа;

2. Реализация принципа умственного развития учащихся;

3. Развитие познавательной и творческой деятельности учащихся;

4. Развитие культуры коллективного умственного труда;

5. Формирование и развитие интереса учащихся к занятиям математикой.

6. Воспитывать ответственность, толерантность во время работы в коллективе, в группах.

Технологии: стратегии творческого поиска: «Принцип дополняемости», «Путь из системы», акмеологическая методика «Преобразующего мышления».

Приемы: поверь в себя, значимости, новизны, дидактическая игра , анонсирования, эврестический прием, прием «Взрыв эмоций», коробка пожеланий.

Оборудование и материалы: компьютер, презентация с рисунками и заданиями конкурса, раздаточный материал.

Форма занятия: дидактическая игра.

Эпиграф: ЧЕЛОВЕК ПОДОБЕН ДРОБИ, ЧИСЛИТЕЛЬ КОТОРОЙ ЕСТЬ ТО, ЧТО ЧЕЛОВЕК ПРЕДСТАВЛЯЕТ СОБОЙ, А ЗНАМЕНАТЕЛЬ- ТО, ЧТО ОН ДУМАЕТ О СЕБЕ! Л.Толстой

Ход урока

Организационный этап.

( Накануне, в каждом классе, учащиеся определяют две команды из 6 человек - смека­листых, любознательны и начитанных. Команду возглавляет капитал. Остальные учащиеся клас­сов - зрители.)

Прием Анонсирования. Состоит в заинтересованности учащихся учебным предметом путем анонсирования темы или формы работы следующего урока. Возможна предварительная работа с учащимися с целью их выступления во время решения отдельных упражнений.

(Учащимся заранее была обьявлена тема игры, перед игрой им необходимо прочитать дополнительную литературу про обыкновенные дроби.)

Вечер начинается торжественно. Под музыку и апло­дисменты входят команды на сцену.

Учитель:

- Сегодня, друзья, мы будем с вами

Царицу наук восхвалять.

Так можем гордо и по праву

Мы математику назвать.

Прием «Поверь в себя.» Учитель создает такие условия, что выполняя задания ученики начинают верить в свои возможности.

Мы начинаем математическое состязание под название «Умницы и умники». Для сегодняшнего мероприятия я приготовила высказывание извесного человека - Конфуция: «От настроения, с которым вы начинаете день или какое-то дело, зависит ваш успех, а может, и неудача». Я желаю вам начать нашу игру с хорошим настроением и получить от нее удовольствие и хорошие результаты. Принимать участие в игре должны все присутствующие: участники игры, болельщики, гости.

Внимание загадка: Она бывает барабанная, а ещё бывает охотничья, и в математике она тоже существует. Что это такое? (Дробь)

И тема нашей игры «Обыкновенные дроби. Действия с обыкновенными дробями»

Эпиграф: ЧЕЛОВЕК ПОДОБЕН ДРОБИ, ЧИСЛИТЕЛЬ КОТОРОЙ ЕСТЬ ТО, ЧТО ЧЕЛОВЕК ПРЕДСТАВЛЯЕТ СОБОЙ, А ЗНАМЕНАТЕЛЬ- ТО, ЧТО ОН ДУМАЕТ О СЕБЕ! Л.Толстой

1. Тур . Кроссворд.

Прием значимости.

Каждая команда получает скрытое слово, которое они смогут разгадать с помощью подсказок, заработанных на конкурсах игры. Команда, которая первой правильно выполняет задание, получает ключ с подсказкой к своему зашифрованному слову. А сейчас участники игры получают карточку с заданиями.

Задание: Разгадайте кроссворд. (приложение 1.)

¹

з

н

а

м

е

н

а

т

е

л

ь

²

д

р

о

б

ь

³

п

р

а

в

и

л

ь

н

а

я

⁴

о

б

ы

к

н

о

в

е

н

н

а

я

⁵

д

р

о

б

н

а

я

⁶

н

е

п

р

а

в

и

л

ь

н

а

я

⁷

ц

е

л

а

я

Вопросы.

1. Число, которое стоит под чертой.

2. Доля или сумма нескольких равных долей.

3. Дробь, у которой числитель меньше знаменателя.

4. Дробь, которая записывается с помощью черты.

5. Какой частью смешенного числа 3 является ?

6. Дробь, у которой числитель больше или равен знаменателю.

7. 1 является …. частью числа 1.

Пока команды трудятся над кроссвордом, ведущий представляет жюри - совет мудрейших. В жюри вхо­дят победители школьных олимпиад, ученики старших классов, некоторые учителя. Оговаривать, какие баллы жюри может присуждать капитанам или болельщикам, не обязательно. Дого­вариваться об оценках нужно в начале мероприятия, а в конце их жюри может согласовывать по ходу работы.

II. Тур. Веселый счет «Дидактическая игра».

Задание 1. Учащиеся обеих команд должны быстро прочитать стихотворение и ответить на вопрос. Бал получает та команда, которая быстро выполнит это задание.

Дроби в математике

я решаю быстро.

Дроби в математике

заставляют мыслить!

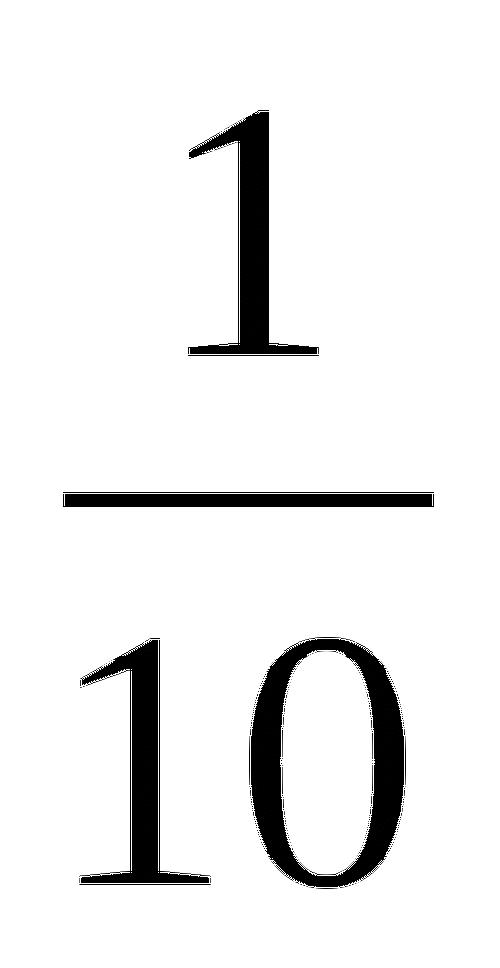
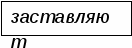
Задание 2. Учитель читает стихотворение с вопросом, учащиеся с места отвечают на вопрос, за каждый правильный ответ получают бал.

Был апельсин всего один.

Но разломали апельсин…

И всем досталось одна седьмая долька,

А нас то было сколько? (Семь)

Борщ поставили погреть.

Сьела дочь кастрюли треть,

А сынок - две трети

Ешьте лучше! Дети!

Остался ли борщ родителям? (Нет)

Два цыпленка прошагали

По дороге треть пути.

Вы б цыплятам подсказали

Сколько им еще идти?

(ответ:две трети)

III. Тур. Сравните дроби.

Команды получают задание. Решив задание, вы узнаете, как в Древнем мире записывали дроби (слайд).

Прием новизны. Включаем в содержание учебного материала интересные сведения, факты, исторические данные.

Интересно знать!!!

Оказывается, еще в древности люди столкнулись с такой же проблемой «Как записать дроби»?. И если бы у нас была машина «времени» и мы оказались бы в Древнем Египте, пол-буханки записали бы с помощью следующего значка (слайд). А в Индии в 4 веке нашей эры (щелчок) пол-буханки записывали следующим образом, где 2 показывает, что буханку нужно разрезать на 2 куска, а 1 говорит о том, что купить вам нужно только одну половинку. Таджикский ученый ал-Насави записал бы пол-буханки вот так (щелчок), где 0 говорит о том, что целых буханок вам покупать не нужно. А вот арабский ученый ал - Хассар в XII в.н.э. придумал записывать пол-буханки вот таким образом (щелчок), такая запись сохранилась по настоящее время. И называются такие числа - обыкновенные дроби.

Задание: Сравните дроби.

и ; и ;

и ; и ;

1 и ; и .

IV. Тур. Дроби и деление.

Задание: Запишите число 6 в виде дроби со знаменателем

а) 1; б) 10; в) 3; г) 9; д) 12; е) 100; ж) 500.

Выполнив это задание, вы узнаете про историю возникновения обыкновенных дробей.

Прием новизны.

Интересно знать!!!

Первое понятие дроби появилось в древнем Египте много веков назад.

Первой дробью, с которой познакомились люди, была половина. Следующей дробью была треть. Это единичные дроби. (½, ¼)

Позже возникновения простых дробей берет свое начало еще в Древней Греции приблизительно во 2 ст. до н. э. Римляне не развинули дальше понятие дроби, т. к. основной дробью у них была унция, то есть 1/12. Дроби 7/12, 8/12, 9/12, … ониназывали 7, 8, 9… унция. Задачу «Что осталось, если от 5 унций вычесть одну унцию?» решали так:

5/12 - 1/12 = 4/12 = 1/3

А на вопрос «Если добавить одну унцию, что получим тогда?» отвечали : «Половину», т. к.

5/12 + 1/12 = 6/12 =1/2

V. Тур. Блиц-турнир «Сокровищница памяти»

Демонстрируется нумерация заданий на сундучке. Учащиеся выбирают число,а учитель зачитывает вопрос, скрытый под этим, ученики сразу отвечают. Неправильные ответы исправляют сами ученики (только при необходимости учитель). За каждый правильный ответ учитель дает каждому ученику смайл с надписью «НИЧЕГО СЕБЕ! УМНЯК!», после опроса ученики отдают под счет свои смайлы жюри.

Вопросы:

1. Как называется число, стоящее над чертой дроби и что оно показывает?

2. Как называется число, стоящее под чертой дроби и что оно показывает?

3. Как можно записать частное от деления натуральных чисел?

4. Каким компонентам деления соответствует числитель и знаменатель?

5. Дать определение обыкновенной дроби?

6. Какое действие означает дробная черта?

7. Как можно получить дробь (два способа)?

8. Какую дробь называют правильной, а какую - неправильной?

9. Дать определение смешанных чисел?

10. Назовите элементы смешанного числа?

11. Как представить дробь в виде смешанного числа?

12. Как представить смешанное число в виде неправильной дроби?

13. Сформулировать правило сложение дробей с одинаковыми знаменателями.

14. Сформулировать правило сложение и вычитание смешанных чисел.

15. Как сравнить правильную дробь и 1?

16. Как сравнить неправильную дробь и 1?

17. Как сравнить правильную и неправильную дробь между собой?

18. Дробь, где числитель равен знаменателю равна…

VI. Тур. Дидактическая игра «Шифровальщик».

Каждая команда получает ряд смешанных чисел, которые они должны представить в виде неправильной дроби , т. е. «зашифровать смешанные числа». Команды обмениваются «шифрованиями» и каждая из команд по данным дробям должны восстановить смешанные числа. После этого команды проверяют друг друга по образцам.

За правильное «шифрование» члены команды получают по 1 балу, за правильную разшифровку - по 2 бала.

VII. Конкурс капита­нов

Дидактическая игра «Шагай - соображай». Участники этого конкурса стоят рядом с ведущим. Все делают первые шаги, и в это время ведущий называет задание: Назвать числа, которые больше 4, но меньше 5. При следующих шагах ребята должны называть дроби, 4 ½ , 4 1/8 и т. д. На каждый шаг - по числу. Ведущий идет с ними в ногу, не давая за­медлить шаг. Как только кто-то ошибся, он остается на месте до конца движения другого.

VIII. Тур. Задачи от Умника.

Акмеологическая методика «Преобразующего мышления». Методика состоит в создании определенных ассоциаций, которые в своем сочетании могут вывести на новую идею.

Задача: Лошадь проскакала 18 км. Найдите 5/6 ее пути.

Ответ: 15 км.

Учитель читает задачу, приводит рисунок к ней и задает наводящие вопросы.

1. Вспомните, что называется дробью.

2. О чем говорит знаменатель дроби? Числитель дроби?

3. сколько километров составит 1/6 часть дороги?

4. А если взять 5 таких частей?

Конкурс для болельщиков

Учитель: У нас есть поговорка "попал в тупик", т.е. попал в такое положение, откуда нет выхода. У немцев есть аналогичная поговорка, которая гласит "попасть в дроби", т.е. попасть в очень трудное положение. Поговорка эта напоминает нам о том времени, когда дроби считались самым трудным и самым запутанным разделом математики. А тот, кто знал дроби, признавался настоящим мудрецом ведущим в математике. Ребята, а вы хотите стать мудрецами?

Учащиеся: Да.

Учитель: Тогда я расскажу вам сейчас одну интересную историю, а вы мне будете в этом помогать. История называется «Мышки, сыр и дроби». Учитель рассказывает историю, а учащиеся называют дроби (слайды).

Эврестический прием. Путем удачно поставленных вопросов педагог наталкивает учащихся на идею решения, нахождения правильного ответа.

(Презентация прилагается)

Подведение итогов.

По результатам всех игр жюри определяет команду, победившую в конкурсах, указы­вает, сколько баллов заработала каждая команда, и поздравляет их.

Наконец команды могут попробовать с помощью подсказок, полученных в результате правильного решения заданий отгадать скрытое слово.

1-я команда. Нидерландский инженер-математик, который впервые систематизировал сведения про обыкновенные дроби. (Стевин)

2-я команда. Фамилия итальянского математика , который впервые использовал дробную черту. (Фибоначчи)

Можно вручить ученикам небольшие шутливые подар­ки. Не надо забывать и побеж­денных - они тоже достойны доброго слова и утеши­тельных призов.

(Прием «Взрыв эмоций». Используя похвалу учитель влияет на эмоциональное состояние ребенка)

Рефлексия деятельности.

Для взаимосвязи учителя и учеников можно использовать прием «Коробка пожеланий».

Ученики пишут ответы на листах и кладут и х в коробку.

− Что понравилось?

− Что не понравилось?

−Что предложите изменить?

(Стратегия творческого поиска «Принцип дополняемости»: ищем объединяющую субстанциональную основу для разных точек зрения, осуществляем соответствующую коррекцию.)

Домашнее задание

(Стратегия творческого поиска «Путь из системы»: предлагаем учащимся индивидуальные творческие задания, которые стимулируют личность для проявления ее внутренней сути, что даст возможность определить направление ее дальнейшего развития.)

1. Обработать буклет про обыкновенные дроби.

Обыкновенные дроби.

Еще в 1735 г. В предисловии к 16-му изданию английской «Арифметики» Уингейта сказано, что в книге изложение арифметики целых чисел, необходимых для расчетов с деньгами для торговли, приводятся раньше, чем открывается доступ к крутым и тяжелым дорогам дробей. Про само воспоминание про них некоторые ученики приходили в такое отчаяние, что останавливались и выкрикивали «Ради, Бога, только не дальше».

2. Изобразить портрет трёх дробей с одинаковыми знаменателями.