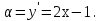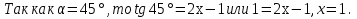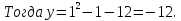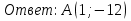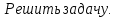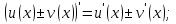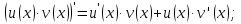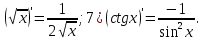Урок по алгебре и началам математического анализа в 11 классе на тему: 'Производная'

МАОУ лицей №44 города Липецка

Учитель математики: Скорикова Людмила Алексеевна

Урок повторения производной в 11 классе

Организации целенаправленного повторения материала по математике я придаю очень большое значение, так как это позволяет привести в систему знания учащихся, делает их более прочными и осознанными.

В 11-м классе при повторении систематизируются знания по всему курсу. Заключительные уроки на повторение тем: «Производная и ее применения», «Первообразная и интеграл» я провожу изучения показательной и логарифмической функций, а потом уже перехожу к изучению производной показательной и логарифмической функций. Это я объясняю темы, что без повторения очень трудно установить связь между давно пройденной темой «Производная» с темой «Производная показательной и логарифмической функции». А обширное повторение этого материала будет способствовать более глубокому пониманию нового.

Повторение организую в виде практических занятий. Основную задачу вижу в повторении теоретического материала, в выработке умений и навыков решения основных типов задач.

Тема «Производная»

Цель: повторить геометрический и физический смысл производной, правила дифференцирования.

1. Рассказать о геометрическом смысле производной (задача с касательной) и решить задачу:

Определить угол, который составляет с осью ОХ касательной к графику функции 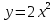в точках с абсциссами 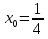и

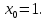
Решение. Находим

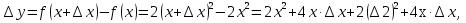
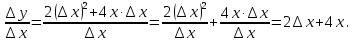
Так как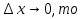

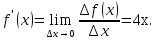
Поэтому

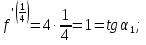
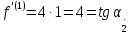
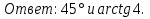
2. Рассказать о физическом смысле производной (задача о скорости) и решить задачу:

Закон прямолинейного движения материальной точки задан зависимостью

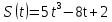
Где s и t измеряются соответственно в метрах и секундах. Найти скорость и ускорение в момент времени t=2c.

Решение. Находим

;

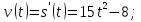
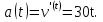
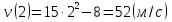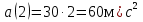
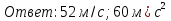
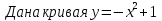. Найти точку ее графика, в которой касательная параллельна прямой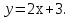

Решение. Так как касательная параллельна прямой

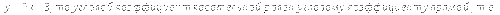
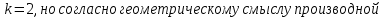
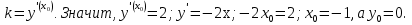
Ответ: (-1;0).

4. Повторить правила дифференцирования:

5. Повторить формулы дифференцирования:

1. C'=0 5)

2. 

4. ;

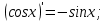
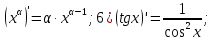
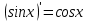Производная сложной функции 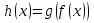находится по формуле

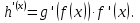
6. Найти производную функции .

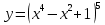Решение

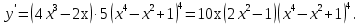
7. Итог урока.

Домашнее задание

1. Повторить уравнение касательной.

2. Найти точки, в которых касательные к кривой 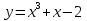параллельны прямой

Y=4x-1.

3. Найти координаты точки, в которой касательная к параболе

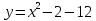образует с осью ОХ угол 45

Решение задач

2.

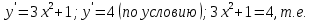
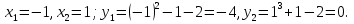
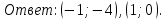
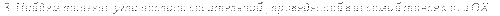
tg