- Учителю
- Рабочая программа по алгебре 8 класс
Рабочая программа по алгебре 8 класс
 РОССИЙСКАЯ ФЕДЕРАЦИЯ
РОССИЙСКАЯ ФЕДЕРАЦИЯ
РОСТОВСКАЯ ОБЛАСТЬ
муниципальное бюджетное общеобразовательное учреждение
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №49
г. Шахты Ростовской области
Рассмотрена и рекомендована к утверждению МО
«___»_____________2013г.
протокол № _______
Руководитель МО __________
Рассмотрена и рекомендована к утверждению педсоветом
«____»______________2013г.
протокол №_________
Утверждена приказом МОУСОШ №49
от ____________ №______
Директор школы
____________
РАБОЧАЯ ПРОГРАММА
учебного курса
по алгебре
для класса 8
на 2013-2014 учебный год
Составитель: Ржевская М.П.
Ф.И.О.
_________________
подпись
I. Пояснительная записка
Рабочая программа учебного курса «Алгебра» для 8 класса разработана на основе федерального компонента государственного образовательного стандарта основного общего образования по математике, «Обязательного минимума содержания основного общего образования по математике» и авторской программы по алгебре Ю. Н. Макарычева, входящей в сборник рабочих программ «Программы общеобразовательных учреждений: Алгебра, 7-9 классы», составитель: Т.А. Бурмистрова «Программы общеобразовательных учреждений: Алгебра , 7-9 классы».- М. Просвещение, 2008. Планирование ориентировано на учебник «Алгебра 8 класс» под редакцией С.А.Теляковского, авторы: Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова, Издательство: М., «Просвещение», 2008-2012 годы.
Рабочая программа выполняет две основные функции:
-
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
-
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Изучение алгебры на ступени основного общего образования направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Задачи учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
В рамках указанных содержательных линий решаются следующие задачи:
-
систематизация сведений о числах; изучение новых видов числовых выражений и формул;
-
совершенствование практических навыков и вычислительной культуры; приобретение практических навыков, необходимых для повседневной жизни;
-
формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности;
-
развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений;
-
развитие воображения, способностей к математическому творчеству;
-
важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры;
-
формирование функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты в простейших прикладных задачах.
Нормативное обеспечение программы:
1.Закон об образовании РФ.
2.Федеральный компонент государственного стандарта общего образования. Стандарт основного общего образования по математике. //Вестник образования России.2004. №12 с.107-119.
3.Обязательный минимум содержания основного общего образования по предмету. (Приказ МО от 19.05.1998 №1276)
4.) Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель Бурмистрова Т. А. - М.: Просвещение, 2008.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры в 8 классе отводится 102 часа из расчёта 3 часа в неделю (1 вариант планирования). На изучение курса в соответствии с программой Бурмистровой Т. А. «Программы общеобразовательных учреждений. Алгебра. 7-9 классы.М.: Просвещение, 2008» (второй вариант планирования) отводится 102 часов (4 часа в неделю). Планирование учебного материала по алгебре рассчитано на 102 учебных часа согласно календарно-тематическому планированию на 2013-14 учебный год. Дополнительные часы используются для расширения знаний и умений по отдельным темам всех разделов курса.
Изменения, внесенные в авторскую учебную программу и их обоснование
В соответствии с планом внутри школьного контроля с целью изучения преподавания предметов, добавлены три контрольные работы: входная контрольная работа (за курс алгебры 7 класса), промежуточная контрольная работа (за I полугодие) и итоговая контрольная работа по тексту администрации за курс 8 класса. В связи с этим, изменено соотношение часов на раздел «Повторение», и вместо предложенных в авторской программе 8 часов, в данной рабочей программе 5 часов. Количество контрольных работ 12.
II. Содержание учебного предмета
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса.
Содержание курса алгебры 8 класса включает следующие тематические блоки:
№
Тема
Количество часов
Контрольных работ
1
Рациональные дроби.
23
2
2
Квадратные корни.
19
2
3
Квадратные уравнения.
21
2
4
Неравенства.
20
2
5
Степень с целым показателем. Элементы статистики.
11
1
Повторение.
5
Контрольные работы по тексту администрации:
-входной контроль
-промежуточный контроль
- итоговая контрольная по тексту администрации
1
1
1
Итого
102ч
12
Характеристика основных содержательных линий
1. Рациональные дроби (23 ч)
Рациональная дробь. Основное свойство дроби, сокращение дробей.
Тождественные преобразования рациональных выражений. Функция 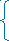 и ее график.
и ее график.
Основная цель - выработать умение выполнять тождественные преобразования рациональных выражений.
Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с учащимися преобразования целых выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.
При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.
Изучение темы завершается рассмотрением свойств графика функции 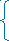 .
.
2. Квадратные корни (19 ч)
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция 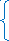 ее свойства и график.
ее свойства и график.
Основная цель - систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные учащимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.
При введении понятия корня полезно ознакомить учащихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество 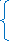 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 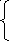
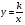 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений учащихся. Рассматриваются функция 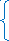 , ее свойства и график. При изучении функции
, ее свойства и график. При изучении функции 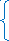 показывается ее взаимосвязь с функцией
показывается ее взаимосвязь с функцией 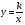 , где x ≥ 0.
, где x ≥ 0.
3. Квадратные уравнения (21 ч)
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Основная цель - выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида ах2 + bх + с = 0, где а ≠ 0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.
4. Неравенства (20 ч)
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Основная цель - ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности.
Умения проводить дедуктивные рассуждения получают развитие, как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.
В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств.
При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ах > b, ах < b, остановившись специально на случае, когда а < 0.
В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.
5. Степень с целым показателем. (11 ч)
Степень с целым показателем и ее свойства. Стандартный вид числа. Приближенный вычисления.
Основная цель - выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях.
В этой теме формулируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
6. Повторение (5 ч)
Планируемые результаты изучения курса алгебры
В результате изучения алгебры в 8 классе ученик должен знать и понимать
- определения основных понятий, изученных в 8 классе, основные формулы сокращенного умножения, обосновывать свои ответы, приводить нужные примеры.
К концу 8 класса учащиеся должны уметь:
-составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через другую;
-выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
-решать линейные, квадратные уравнения по общей формуле корней квадратного уравнения и теореме Виета, рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
-решать линейные с одной переменной и их системы;
-решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-изображать числа точками на координатной прямой;
-определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
-находить значения функции, заданной формулой, таблицей, графиком по её аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей; знать свойства функций y=k/х, у=х2.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
-выполнения расчётов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
-моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
-описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
Элементы статистики
-извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
-вычислять средние значения результатов измерений;
-находить частоту события, используя собственные наблюдения и готовые статистические данные;
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
-анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объёмов, времени, скорости;
-понимания статистических утверждений.
Требования к уровню подготовки обучающихся в 8 классе.
В результате изучения алгебры ученик должен
-
знать/понимать
-
существо понятия математического доказательства; примеры доказательств;
-
существо понятия алгоритма; примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
-
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
-
уметь
-
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
-
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
-
решать линейные неравенства с одной переменной и их системы;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
-
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
-
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
-
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами.
Контрольно-измерительный материал.
Контрольные работы составляются с учетом обязательных результатов обучения.
Тексты контрольных работ взяты из:
-
Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель Бурмистрова Т. А. - М.: Просвещение, 2008;
-
Алгебра. Дидактические материалы. 8 класс / Ю.Н.Макарычев, Н.Г.Миндюк, Л.Б.Крайнева.. - М.: Просвещение, 2011.
Система оценивания.
Оценивание соответствует идее дифференциации обучения.
Самостоятельные работы, математический диктант, тесты составляются из заданий разного уровня сложности (обязательного и повышенного). Тексты контрольных работ состоят из двух частей: обязательного и повышенного уровня. Верное выполнение заданий обязательного уровня оценивается оценкой не выше удовлетворительной.
Оценки за самостоятельные работы, тесты, математические диктанты, домашние работы выставляются выборочно, по согласованию с учащимися.
III. Календарно-тематическое планирование по алгебре 8 «Б» класс (3 часа в неделю)
-
Дата по плану
Дата фактическая
№
п/п
Тема урока
Виды учебной
деятельности
Виды контроля
Глава 1. Рациональные дроби. 23 ч + 1 к
§1. Рациональные дроби и их свойства.
1
1. Рациональные выражения.
Работа с учебником
ИДР
2
1. Рациональные выражения.
Индивидуальная работа с самооценкой.
ИРК
3
2. Основное свойство дроби. Сокращение дробей.
Составление опорного конспекта
ИДР
4
2. Основное свойство дроби. Сокращение дробей.
Решение выражений с комментированием
ФО, ИДР
5
2. Основное свойство дроби. Сокращение дробей.
Учебная практическая работа в парах
СР
6
Контрольная работа по тексту администрации (входная)
§2. Сумма и разность дробей.
7
3. Сложение и вычитание дробей с одинаковыми знаменателями.
Составление опорного конспекта
ФО
8
3. Сложение и вычитание дробей с одинаковыми знаменателями.
Учебная практическая работа в парах
ФО, СР
9
4. Сложение и вычитание дробей с разными знаменателями.
Работа с учебником
ИДР
10
4. Сложение и вычитание дробей с разными знаменателями.
Решение выражений с комментированием
СР
11
4. Сложение и вычитание дробей с разными знаменателями.
Учебная практическая работа в парах
ФО
12
Обобщающий урок по теме «Рациональные выражения. Сумма и разность дробей»
Индивидуальная работа с самооценкой.
ИРК
13
Контрольная работа №1 по теме «Рациональные выражения. Сложение и вычитание дробей»
§3. Произведение и частное дробей.
14
5. Умножение дробей. Возведение дроби в степень.
Составление опорного конспекта
ИДР
15
5. Умножение дробей. Возведение дроби в степень.
Индивидуальная работа с самооценкой.
ФО, ОСР
16
6. Деление дробей.
Работа с учебником
ИДР
17
6. Деление дробей.
Учебная практическая работа в парах
ФО, ОСР
18
7. Преобразование рациональных выражений.
Составление опорного конспекта
ФО
19
7. Преобразование рациональных выражений.
Учебная практическая работа в парах
ИДР
20
7. Преобразование рациональных выражений.
Индивидуальная работа с самооценкой.
ФО, СР
21
8. Функция у = k / x и ее график.
Составление опорного конспекта
ФО, ИРК
22
8. Функция у = k / x и ее график.
Индивидуальная работа с самооценкой.
Т
23
Обобщающий урок по теме «Произведение и частное дробей»
Работа с учебником
ОСР
24
Контрольная работа № 2 по теме «Произведение и частное дробей»
Глава 2. Квадратные корни. 19 ч
§4. Действительные числа.
25
10. Рациональные числа.
Работа с учебником
ИДР
26
11. Иррациональные числа.
Работа с учебником
ФО, ИДР
§5. Арифметический квадратный корень.
27
12. Квадратные корни. Арифметический квадратный корень.
Работа с учебником
ФО, ИДР
28
13. Уравнение х2 = а.
Учебная практическая работа в парах
ОСР
29
14. Нахождение приближенных значений квадратного корня.
Работа с учебником
ФО
30
15. Функция у = √х и ее график.
Составление опорного конспекта
ИРК
31
15. Функция у = √х и ее график.
Индивидуальная работа с самооценкой.
ДРЗ
§6. Свойства арифметического квадратного корня.
32
16. Квадратный корень из произведения и дроби.
Работа с учебником
ФО, ИДР
33
16. Квадратный корень из произведения и дроби.
Учебная практическая работа
ОСР
34
17. Квадратный корень из степени.
Индивидуальная работа с самооценкой.
Т
35
Контрольная работа №3 по теме ««Квадратные корни»
§7. Применение свойств арифметического квадратного корня.
36
18. Вынесение множителя из-под знака корня. Внесение множителя под знак корня.
Работа с учебником
ФО, ИДР
37
18. Вынесение множителя из-под знака корня. Внесение множителя под знак корня.
Учебная практическая работа в парах
СР
38
18. Вынесение множителя из-под знака корня. Внесение множителя под знак корня.
Индивидуальная работа с самопроверкой
ДРЗ
39
19. Преобразование выражений, содержащих квадратные корни.
Работа с учебником
ФО, ИДР
40
19. Преобразование выражений, содержащих квадратные корни.
Учебная практическая работа в парах
ФО, ДРЗ
41
19. Преобразование выражений, содержащих квадратные корни.
Работа с учебником
Т
42
Обобщающий урок по теме «Применение свойств арифметического квадратного корня»
Индивидуальная работа с самопроверкой
ОСР
43
Контрольная работа № 4 «Применение свойств арифметического квадратного корня»
Глава 3. Квадратные уравнения. 21 ч
§8. Квадратное уравнение и его корни. 10
44
21. Неполные квадратные уравнения.
Работа с учебником
ФО, ИДР
45
21. Неполные квадратные уравнения.
Учебная практическая работа в парах
ОСР
46
22. Формула корней квадратного уравнения.
Индивидуальная работа с самопроверкой
ФО, ИДР
47
22. Формула корней квадратного уравнения.
Решение уравнений с комментированием
ИРК
48
Контрольная работа по тексту администрации (промежуточная)
49
22. Решение квадратных уравнений по формуле.
Учебная практическая работа в парах
СР
50
23. Решение задач с помощью квадратных уравнений.
Работа с учебником
ФО, ИДР
51
23. Решение задач с помощью квадратных уравнений.
Индивидуальная работа с самопроверкой
ДРЗ
52
24. Теорема Виета.
Решение задач с комментированием
ИДР
53
24. Теорема Виета.
Учебная практич работа в парах
ИДР
54
Обобщающий урок по теме «Квадратные уравнения»
Работа с учебником
Т
55
Контрольная работа №5 по теме «Квадратные уравнения»
§9. Дробные рациональные уравнения. 9
56
25. Решение дробных рациональных уравнений.
Работа с учебником
ИДР
57
25. Решение дробных рациональных уравнений.
Учебная практическая работа в парах
СР
58
25. Решение дробных рациональных уравнений.
Индивидуальная работа с самопроверкой
ДРЗ
59
Решение дробных рациональных уравнений.
Решение задач с комментированием
ИДР
60
26. Решение задач с помощью рациональных уравнений.
Индивидуальная работа
ДРЗ
61
26. Решение задач с помощью рациональных уравнений.
Учебная практическая работа в парах
ФО, ИДР
62
Решение задач с помощью рациональных уравнений.
Индивидуальная работа с самопроверкой
СР
63
Решение задач с помощью рациональных уравнений.
Работа с учебником
ДРЗ
64
Обобщающий урок по теме «Дробные рациональные уравнения»
Индивидуальная работа с самопроверкой
Т
65
Контрольная работа № 6 по теме «Дробные рациональные уравнения»
Глава 4. Неравенства. 20 ч
§10. Числовые неравенства и их свойства. 8
66
28. Числовые неравенства.
Составление опорного конспекта
ФО, ИДР
67
28. Числовые неравенства.
Работа с учебником
ИРК
68
29. Свойства числовых неравенств.
Составление опорного конспекта
ФО, ИДР
69
29. Свойства числовых неравенств.
Работа с учебником
ФО, ОСР
70
30. Сложение и умножение числовых неравенств
Учебная практическая работа в парах
ИДР
71
30. Сложение и умножение числовых неравенств
Индивидуальная работа с самооценкой.
ДРЗ
72
30. Сложение и умножение числовых неравенств
Решение выражений с комментированием
ФО, СР
73
31. Погрешность и точность приближения.
Работа с учебником.
ФО
74
Контрольная работа №7 по теме «Числовые неравенства и их свойства»
§11. Неравенства с одной переменной и их системы. 10
75
32. Пересечение и объединение множеств.
Работа с учебником.
ФО, Т
76
33. Числовые промежутки.
Учебная практическая работа в парах
ФО, Т
77
33. Числовые промежутки.
Индивидуальная работа с самооценкой.
СР
78
34. Решение неравенств с одной переменной.
Работа с учебником.
ФО, ИДР
79
34. Решение неравенств с одной переменной.
Учебная практическая работа в парах
ОСР
80
34. Решение неравенств с одной переменной.
Индивидуальная работа с самооценкой.
ДРЗ
81
35. Решение систем неравенств с одной переменной.
Решение неравенств с комментированием
Т
82
35. Решение систем неравенств с одной переменной.
Работа с учебником.
ИДР
83
35. Решение систем неравенств с одной переменной.
Учебная практическая работа в парах
ФО, ИРК
84
Обобщающий урок по теме «Неравенства с одной переменной и их системы»
Индивидуальная работа с самооценкой.
ДРЗ
85
Контрольная работа №8 по теме «Неравенства с одной переменной и их системы»
Глава 5. Степень с целым показателем. Элементы статистики. 11 ч
§12. Степень с целым показателем и её свойства. 6
86
37. Определение степени с целым отрицательным показателем.
Составление опорного конспекта
ФО, ИДР
87
37. Определение степени с целым отрицательным показателем.
Учебная практическая работа в парах
ИРК
88
38. Свойства степени с целым показателем.
Составление опорного конспекта
ФО, ИДР
89
38. Свойства степени с целым показателем.
Индивидуальная работа с самооценкой.
СР
90
39. Стандартный вид числа.
Учебная практическая работа в парах
ФО, ИДР
91
39. Стандартный вид числа.
Работа с учебником
ИРК
92
Контрольная работа №9 по теме «Степень с целым показателем»
§13. Элементы статистики. 4
93
40. Сбор и группировка статистических данных.
Составление опорного конспекта
ИДР
94
40. Сбор и группировка статистических данных.
Работа с учебником
ИРК
95
41. Наглядное представление статистической информации
Учебная практическая работа в парах
ИДР
96
41. Наглядное представление статистической информации
Индивидуальная работа с самооценкой.
ИРК
97
Итоговая контрольная работа по тексту администрации.
ИК
Повторение. 5 7 ч
98
Повторение «Рациональные дроби»
Практикум решения выражений
ДРЗ
99
Повторение «Квадратные корни. Квадратные уравнения»
Индивидуальная работа с самопроверкой
Т
100
Повторение «Неравенства»
Практикум решения неравенств
СР
101
Повторение . Степень с целым показателем.
Учебная практическая работа в парах
102
Урок обобщения и систематизации изученного материала
ОСР - обучающая самостоятельная работа
ФО- фронтальный опрос
ИДР - индивидуальная работа у доски
ТЗ - творческое задание
ИРК - индивидуальная работа по карточкам
СР - самостоятельная работа
ПР - проверочная работа
Т - тестовая работа
ИК - индивидуальный контроль
V. Материально-техническое обеспечение
образовательного процесса по алгебре
Источники информации для учителя
1. Алгебра. 8 класс: поурочные планы по учебнику Ю.Н. Макарычева и др. / авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. - Волгоград: Учитель, 2007. - 303 с.
2. Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского. М.: Просвещение, 2002.
3. Государственный стандарт основного общего образования по математике.
4. Дидактические материалы по алгебре для 8 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. - М.: Просвещение, 2006. - 144 с.
5. Живая математика. Учебно-методический комплект. Версия 4.3. Программа. Компьютерные альбомы. М: ИНТ.
6. Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель: Бурмистрова Т.А. - М.: Просвещение, 2008 г.
7. - единая коллекция цифровых образовательных ресурсов.
Источники информации для учащихся
1. Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского. М.: Просвещение, 2002.
2. Дидактические материалы по алгебре для 8 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. - М.: Просвещение, 2006. - 144 с.
3. Живая математика. Учебно-методический комплект. Версия 4.3. Программа. Компьютерные альбомы. М: ИНТ.
Технические средства обучения:
1) Компьютер.
2) Видеопроектор
Информационно-коммуникативные средства:
-
Тематические презентации
-
Компакт-диск Алгебра, 9 класс: поурочные планы по учебнику Ю.Н. Макарычева «Учитель», 2010.
Интернет- ресурсы:
http://www.prosv.ru - сайт издательства «Просвещение» (рубрика «Математика»)
www.drofa.ru - сайт издательства Дрофа (рубрика «Математика»)
- методические рекомендации учителю-предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе.
- Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента, сервер информационной поддержки Единого государственного экзамена.
- сайт Интернет - школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, включают подготовку сдачи ЕГЭ, ГИА.
- сайт издательства «Легион»
- сайт издательства «Интеллект-Центр», где можно найти учебно-тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений
- портал информационной поддержки мониторинга качества образования, здесь можно найти Федеральный банк тестовых заданий.
Контрольно - измерительные материалы по алгебре 8 класса.
Контрольная работа №1 по теме:
«Рациональные выражения. Сложение и вычитание дробей»
Вариант - 1
1. Сократите дробь:
а) 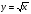 б)
б) 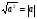 ; в)
; в) 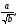
2. Представьте в виде дроби:
а) 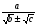 б)
б) 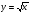
в) 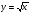 .
.
3. Найдите значение выражения 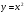 при а = 0,2; в = -5.
при а = 0,2; в = -5.
4. Упростите выражение
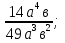 .
.
Вариант - 2
1. Сократите дробь:
а) 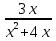 б)
б) 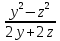 ; в)
; в) 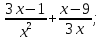
2. Представьте в виде дроби:
а) 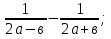 б)
б) 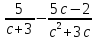
в) 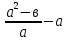 .
.
3. Найдите значение выражения 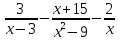 при х = - 8, у = 0,1.
при х = - 8, у = 0,1.
4. Упростите выражение
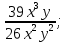 .
.
Контрольная работа №2 по теме
«Произведение и частное дробей»
Вариант - 1
1. Представьте в виде дроби:
а) 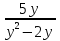 б)
б) 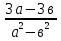
в) 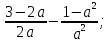 г)
г) 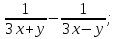
2. Постройте график функции у = 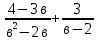 . Какова область определения функции? При каких значениях Х функция принимает отрицательные значения?
. Какова область определения функции? При каких значениях Х функция принимает отрицательные значения?
3. Докажите, что при всех значениях b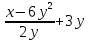
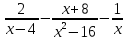 1 значения выражения не зависят от b.
1 значения выражения не зависят от b.
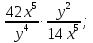
Вариант - 2
1. Представьте в виде дроби:
а) 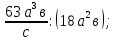 б)
б) 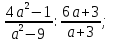
в) 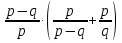 г)
г) 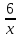
2. Постройте график функции у = 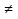 . Какова область определения функции? При каких значениях Х функция принимает положительные значения?
. Какова область определения функции? При каких значениях Х функция принимает положительные значения?
3. Докажите, что при всех значениях х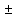 2 значения выражения не зависят от b.
2 значения выражения не зависят от b.
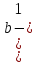
Контрольная работа №3 по теме
«Квадратные корни»
Вариант - 1
1. Вычислите:
а) 0,5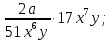 б) 2
б) 2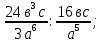
в) 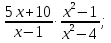
2. Найдите значение выражения:
а) 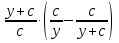 б)
б) 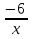
в) 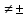 г)
г) 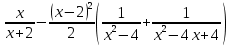
3. Решите уравнение: а) 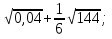
б) 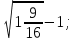
4. Упростите выражение:
а) 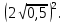 б)
б) 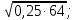
5. Укажите два последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число 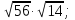
6. Имеет ли корни уравнение 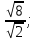 + 1 = 0 ?
+ 1 = 0 ?
Вариант - 2
1. Вычислите:
а) 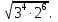 б)
б) 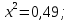
в) 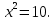
2. Найдите значение выражения:
а) 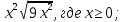 б)
б) 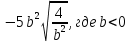
в) 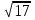 г)
г) 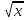
3. Решите уравнение: а) 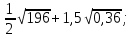
б) 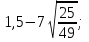
4. Упростите выражение:
а) 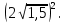 б)
б) 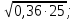
5. Укажите два последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число 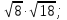
6. Имеет ли корни уравнение 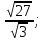 = 1 ?
= 1 ?
Контрольная работа №4 по теме
«Применение свойств арифметического квадратного корня»
Вариант - 1
1. Упростите выражение:
а) 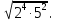
б) 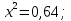
в) (3 - 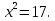 .
.
2. Сравните: 7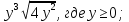
3. Сократите дробь:
а) 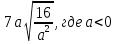 б)
б) 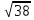
4. Освободите дробь от знака корня в знаменателе: а) 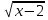
5) Докажите, что значение выражения
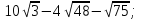 есть число рациональное.
есть число рациональное.
Вариант - 2
1. Упростите выражение:
а) 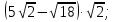
б) 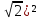
в) (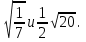 +
+ 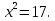 .
.
2. Сравните: 10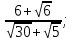
3. Сократите дробь:
а) 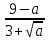 б)
б) 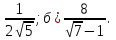
4. Освободите дробь от знака корня в знаменателе: а) 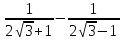
5) Докажите, что значение выражения
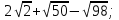 есть число рациональное.
есть число рациональное.
Контрольная работа №5 по теме
«Квадратные уравнения»
Вариант - 1
1. Решите уравнение:
а) 2х² + 7х - 9 = 0; б) 3х² = 18х;
в) 100х² - 16 = 0; г) х² - 16х + 63 = 0.
2. Периметр прямоугольника равен 20 см. Найдите его стороны, если известно, что площадь прямоугольника равна 24 см².
3. В уравнении х² + pх - 18 = 0 равен -9. Найдите другой корень и коэффициент р.
Вариант - 2
1. Решите уравнение:
а) 3х² + 13х - 10 = 0; б) 2х² - 3х = 0;
в) 16х² = 49; г) х² - 2х - 35 = 0.
2. Периметр прямоугольника равен 30 см. Найдите его стороны, если известно, что площадь прямоугольника равна 56 см².
3. Один корень уравнения х² + 11х + q = 0 равен -7. Найдите другой корень и свободный член q.
Контрольная работа №6 по теме
«Дробные рациональные уравнения»
Вариант - 1
1. Решите уравнение:
а) 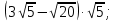 ; б)
; б) 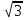 .
.
2. Из пункта А в пункт В велосипедист проехал по одной дороге, длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он всё же на обратный путь затратил времени на 10 мин меньше, чем на путь их А в В. С какой скоростью ехал велосипедист из А в В?
Вариант - 2
1. Решите уравнение:
а) 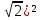 ; б)
; б) 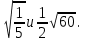 .
.
2. Катер прошёл 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шёл 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч?
Контрольная работа №7 по теме
«Числовые неравенства и их свойства»
Вариант - 1
1. Докажите неравенство:
а) (х - 2)² > х (х - 4);
б) а² + 1 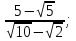 2(3а - 4).
2(3а - 4).
2. Известно, что а < в. Сравните:
а) 21а и 21в; б) -3,2а и -3,2в; в) 1,5в и 1,5а.
Результат сравнения запишите в виде неравенства.
3. Известно, что 2,6 < 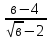 Оцените:
Оцените:
а) 2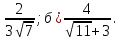 б) -
б) - 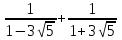
4. Оцените периметр и площадь прямоугольника со сторонами а см и b см, если известно, что 2,6 < a < 2,7, 1,2 < b < 1,3.
5. К каждому из чисел 2, 3, 4 и 5 прибавили одно и то же число a. Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
Вариант - 2
1. Докажите неравенство:
а) (х + 7)² > х (х + 14);
б) в² + 5 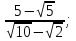 10(в - 2).
10(в - 2).
2. Известно, что а > в. Сравните: а) 18а и 18в; б) -6,7а и -6,7в; в) -3,7в и -3,7а.
Результат сравнения запишите в виде неравенства.
3. Известно, что 3,1 < 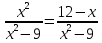 Оцените:
Оцените:
а) 3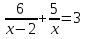 б) -
б) - 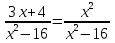
4. Оцените периметр и площадь прямоугольника со сторонами а см и b см, если известно, что 1,5 < a < 1,6, 3,2 < b < 3,3.
5. Даны четыре последовательных натуральных числа. Сравните произведение первого и последнего из них с произведением двух средних чисел.
Контрольная работа №8 по теме
«Неравенства с одной переменной и их системы»
Вариант - 1
1. Решите неравенство:
а) 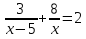 б) 1 - 3х
б) 1 - 3х 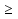 0;
0;
в) 5(у - 1,2) - 4,6 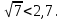 3у + 1.
3у + 1.
2. При каких значениях а значение дроби 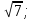 меньше соответствующего значения дроби
меньше соответствующего значения дроби 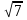 ?
?
3. Решите систему неравенств:
а) 2х - 3 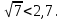 0, б) 3 - 2х < 0,
0, б) 3 - 2х < 0,
7х + 4 > 0. 1,6 + х < 2,9.
4. Найдите целые решения системы неравенств:
6 - 2х < 3(х - 1),
6 - 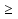
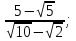 х.
х.
5. При каких значениях х имеет смысл выражение 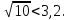 ?
?
Вариант - 2
1. Решите неравенство:
а) 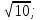 б) 2 - 7х > 0;
б) 2 - 7х > 0;
в) 6(у - 1,5) - 3,4 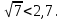 4у - 2,4.
4у - 2,4.
2. При каких значениях в значение дроби 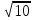 больше соответствующего значения дроби
больше соответствующего значения дроби 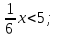 ?
?
3. Решите систему неравенств:
а) 4х - 10 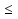 0, б) 1,4 + х > 1,5,
0, б) 1,4 + х > 1,5,
3х - 5 > 1. 5 - 2х > 2.
4. Найдите целые решения системы неравенств:
10 - 4х < 3(1 - х),
3,5 + 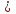
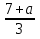 х.
х.
5. При каких значениях х имеет смысл выражение 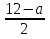 ?
?
Контрольная работа №9 по теме
«Степень с целым показателем»
Вариант - 1
1. Найдите значение выражения:
а) 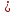
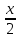
2. Упростите выражение:
а) 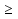
3. Преобразуйте выражение:
а) 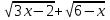
4. Вычислите:
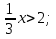
5. Найдите приближённые значения суммы и разности чисел х и у, если х 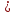
6. Найдите приближённые значения произведения и частного чисел а и в, если а 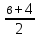 6,124
6,124 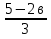
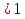
Вариант - 2
1. Найдите значение выражения:
а) 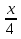
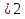
2. Упростите выражение:
а) 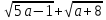
3. Преобразуйте выражение:
а) 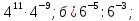
4. Вычислите:
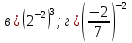
5. Найдите приближённые значения суммы и разности чисел а и в, если а 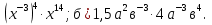
6. Найдите приближённые значения произведения и частного чисел х и у, если х 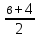 8,136
8,136 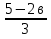
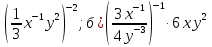
2