- Учителю
- ИТОГОВАЯ ПРАКТИКО-ЗНАЧИМАЯ РАБОТА Реализация требований ФГОС ООО при обучении учащихся 5 класса теме: “Обыкновенные дроби”
ИТОГОВАЯ ПРАКТИКО-ЗНАЧИМАЯ РАБОТА Реализация требований ФГОС ООО при обучении учащихся 5 класса теме: “Обыкновенные дроби”
ГБОУ ВПО МО «Академия социального управления»
дополнительное профессиональное образование
кафедра математических дисциплин
ИТОГОВАЯ ПРАКТИКО-ЗНАЧИМАЯ РАБОТА
Реализация требований ФГОС ООО при обучении учащихся 5 класса
теме: "Обыкновенные дроби"
Учебник: Виленкин Н.Я.. Математика. 5 класс.
Выполнил слушатель учебного курса
«Актуальные проблемы развития профессиональной компетентности учителя математики (в условиях реализации ФГОС)»
учитель математики МАОУ
Селятинской СОШ №, Наро-Фоминского района.
САЗАНОВА Татьяна Вячеславовна.
Руководитель курса: заведующая кафедрой ВАСИЛЬЕВА Марина Викторовна, кандидат педагогических наук
Москва 2015г.
Содержание
Стр.
ВВЕДЕНИЕ ……………………………………………………
ГЛАВА 1. Теоретические основы обучения теме «Обыкновенные дроби»…………………………………………
§ 1. Требования ФГОС ООО к школьному курсу математики…
§ 2. Логико-дидактический анализ содержания темы …………
§ 3. Примеры решения типовых заданий и задач по теме, направленных на развитие и формирование УУД…………
ГЛАВА 2. Методические рекомендации обучения теме «Обыкновенные дроби»…………………………………………
§ 4. Диагностические цели обучения теме «Обыкновенные дроби»…………………………………………………………….
4.1.Таблица целей обучения теме «Обыкновенные дроби»…
4.2.Карта изучения темы и её использование…………………
§ 5. Учебный план темы……………………………………………
§ 6. Примеры реализации целей обучения теме………………….
ЗАКЛЮЧЕНИЕ………………………………………………….
Список литературы………………………………………………
Приложение………………………………………………………
3
4
4-8
8-12
13-14
17
17
17-18
19-23
24-37
38-51
57
58
ВВЕДЕНИЕ.
Актуальность.
Введение ФГОС - это новый, революционный этап модернизации российского образования. В связи с изменениями, происходящими в современном обществе, выдвигаются новые требования к системе школьного обучения. Изменение приоритетов, когда академичность обучения заменяется умением учиться в силу личных способностей. Любой выпускник должен быть подготовленным к будущей жизни и стать успешным в ней.
Цель работы: Реализация требований ФГОС ООО при изучении темы: «Обыкновенные дроби»
Для достижения поставленной цели необходимо решение следующих задач.
Задачи исследования.
1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС ООО.
2. Выполнить отбор средств обучения теме, в том числе средства ИКТ
3. Разработать таблицу целей и карту обучения теме.
4. Составить фрагмент учебной рабочей программы «Поурочное планирование образовательных результатов освоения математики» .
5. Разработать методические рекомендации обучения теме и применить их в учебном процессе
Решение поставленных задач потребовало использования следующих
методов исследования:
-
изучение концепции духовно - нравственного развития и воспитания личности гражданина России,
-
анализ психолого - педагогической, математической и методической литературы по теме исследования,
-
анализ учебников и учебных пособий по математике;
-
беседы с учителями, тестирование учащихся, проведение опытной проверки.
ГЛАВА 1. Теоретические основы обучения теме «Обыкновенные дроби»
1.1. «Концепция духовно-нравственного развития и воспитания личности гражданина России»
Концепция является методологической основой разработки и реализации федерального государственного образовательного стандарта общего образования.
Концепция представляет собой ценностно-нормативную основу взаимодействия общеобразовательных учреждений с другими субъектами социализации - семьей, общественными организациями, религиозными объединениями, учреждениями дополнительного образования, культуры и спорта, средствами массовой информации. Целью этого взаимодействия является совместное обеспечение условий для духовно-нравственного развития и воспитания обучающихся.
Концепция определяет:
-
характер современного национального воспитательного идеала;
-
цели и задачи духовно-нравственного развития и воспитания детей и молодежи;
-
систему базовых национальных ценностей, на основе которых возможна духовно-нравственная консолидация многонационального народа Российской Федерации;
-
основные социально-педагогические условия и принципы духовно-нравственного развития и воспитания обучающихся.
Современный национальный воспитательный идеал - это высоконравственный, творческий, компетентный гражданин России, принимающий судьбу Отечества как свою личную, осознающий ответственность за настоящее и будущее своей страны, укорененный в духовных и культурных традициях многонационального народа Российской Федерации.
Программы духовно-нравственного развития и воспитания школьников, разрабатываемые и реализуемые общеобразовательными учреждениями совместно с другими субъектами социализации должны обеспечивать полноценную и последовательную идентификацию обучающегося с семьей, культурно-региональным сообществом, многонациональным народом Российской Федерации, открытым для диалога с мировым сообществом.
Организация социально открытого пространства духовно-нравственного развития и воспитания личности гражданина России, нравственного уклада жизни обучающихся осуществляется на основе:
-
нравственного примера педагога;
-
социально-педагогического партнерства;
-
индивидуально-личностного развития;
-
интегративности программ духовно-нравственного воспитания;
Духовно-нравственное развитие и воспитание обучающихся должны быть интегрированы в основные виды деятельности обучающихся: урочную, внеурочную, внешкольную и общественно полезную.
Каждая из базовых ценностей, педагогически определяемая как вопрос, превращается в воспитательную задачу. Для ее решения, обучающиеся вместе с педагогами, родителями, иными субъектами духовной, культурной, социальной жизни обращаются к содержанию:
-
истории России, российских народов, своей семьи, рода;
-
жизненного опыта своих родителей, предков;
-
традиционных российских религий;
-
произведений литературы и искусства, лучших образцов отечественной и мировой культуры;
-
периодической литературы, СМИ, отражающих современную жизнь;
-
фольклора народов России;
-
общественно полезной и личностно значимой деятельности;
-
учебных дисциплин;
-
других источников информации и научного знания.
Базовые ценности не локализованы в содержании отдельного учебного предмета, формы или вида образовательной деятельности. Они пронизывают все учебное содержание, весь уклад школьной жизни, всю многоплановую деятельность школьника как человека, личности, гражданина.
Система базовых национальных ценностей создает смысловую основу пространства духовно-нравственного развития личности. В этом пространстве снимаются барьеры между отдельными учебными предметами, между школой и семьей, школой и обществом, школой и жизнью.
-
социальной востребованности воспитания.
Очевидной является необходимость социальной востребованности воспитания. Воспитание, чтобы быть эффективным, должно быть востребованным в жизни ребенка, его семьи, других людей, общества. Духовно-нравственное развитие достигает содержательной полноты и становится актуальным для самого обучающегося, когда соединяется с жизнью, реальными социальными проблемами, которые необходимо решать на основе морального выбора. Программы духовно-нравственного развития и воспитания должны предусматривать добровольное и посильное включение обучающихся в решение реальных социальных, экологических, культурных, экономических и иных проблем семьи, школы, села, района, города, области, республики, России.
1.2. Требования ФГОС ООО к школьному курсу математики
Следствием внешних и внутренних тенденций в развитии общества и образования явилась разработка стандартов второго поколения. Федеральный государственный образовательный стандарт основного общего образования (далее - Стандарт) представляет собой совокупность требований, обязательных при реализации основной образовательной программы основного общего образования образовательными учреждениями, имеющими государственную аккредитацию.
Методологической основой разработки и реализации Стандарта является Концепция духовно-нравственного развития и воспитания личности гражданина России.
Стандарт устанавливает требования к результатам освоения обучающимися основной образовательной программы основного общего образования: личностным, метапредметным, предметным.
Личностные результаты включают сформированность мотивации к обучению и целенаправленной познавательной деятельности, системы значимых социальных и межличностных отношений, ценностно-смысловых установок.
Метапредметные результаты включают регулятивные, познавательные, коммуникативные способности, их использования в учебной, познавательной и социальной практике.
Предметные результаты включают не только изучение учебного предмета, но и умения, специфические для данной предметной области, виды деятельности по получению нового знания в рамках учебного предмета.
Математическое образование, являясь важнейшим компонентом в системе общего образования и частью общей культуры, обладает уникальными составляющими:
интеллектуально развивающей - изучение математики является источником и средством активного интеллектуального развития человека, его умственных способностей;
познавательной - с помощью математики человек познает окружающий мир, его пространственные и количественные отношения;
прикладной - математика является той базой, которая обеспечивает готовность человека к овладению смежными дисциплинами, многими профессиями, делает для него доступным непрерывное образование и самообразование во многих сферах человеческой деятельности, в немалой степени обеспечивает многие ежедневные потребности человека;
историко-культурологической - на примерах из истории развития математики прослеживается развитие не только основных идей и методов самой математики и их влияние на культурный облик человечества, но и развитие человеческой культуры в целом;
воспитательной - математическое образование воспитывает культуру мышления и способствует формированию важнейших черт нравственной личности,
философско-мировоззренческой - математика помогает осмыслять мир, в котором мы живем, формирует у человека развивающиеся научные представления о строении Вселенной, о реальном физическом пространстве, она все в большей и большей степени становится методом мышления, применяемым во многих науках и научно-технической деятельности.
ФГОС побуждает учителя:
-
развивать у обучающихся широкие познавательные интересы, инициативу и любознательность, мотивы познания и творчества;
-
формировать целеустремленность и настойчивость в достижении целей, готовность к преодолению трудностей и жизненного оптимизма;
-
формировать умение учиться и способность к организации своей деятельности (планировать, корректировать, контролировать и оценивать свою деятельность).
§ 2. Логико-дидактический анализ содержания темы «Обыкновенные дроби»
При изучении математики 5 часов в неделю в 5 классе на тему «Обыкновенные дроби» отводится 22 часа. Согласно программе данная тема включает в себя следующие разделы:
-
Окружность и круг.
-
Доли. Обыкновенные дроби.
-
Сравнение дробей.
-
Правильная и неправильная дробь.
-
Сложение и вычитание дробей с одинаковыми знаменателями.
-
Деление и дроби.
-
Смешанные числа.
-
Сложение и вычитание смешанных чисел.
Основная цель - познакомить учащихся с понятием дроби в объеме, достаточном для введения дробей.
В данной теме изучаются сведения о дробных числах, необходимые для введения десятичных дробей. Среди формируемых умений основное внимание должно быть привлечено к сравнению дробей с одинаковыми знаменателями, к выделению целой части числа. С пониманием смысла дроби связаны три основные задачи на дроби, осознанного решения которых важно добиться от учащихся.
§ 2. Логико-математический анализ содержания темы
-
Формулировка определения
Логический анализ
Подведение под понятие
Следствие из определения
Возможные ошибки
Термин
Род
Видовые отличия
Логические связи
Вид определения
Опорные знания
1.Мама купила арбуз и разделила его на 6 равных частей. Эти равные части называют долями
доля
дробь
запись
конъюнктивная
через род и видовые отличия
деление
деление целого на части
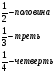
Куда записывать делимое и делитель
2. Запись вида
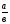 называют обыкновенными дробями
называют обыкновенными дробями
обыкновенная дробь
части
запись
конъюнктивная
через род и видовые отличия
доля
деление целого на части
Изображение дробей на координатной прямой
Что показывает знаменатель и что показывает числитель
3. Дробь, в которой числитель меньше знаменателя, называют правильной дробью.
Дробь, в которой числитель больше знаменателя или равен ему называют неправильной дробью.
правильна и неправильная дробь
дробь
дробь определяется данным знаменателем по отношению к числителю
конъюнктивная
через род и видовые отличия
понятие числителя и знаменателя
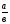
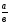 - числитель
- числитель 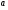 -знаменатель
-знаменатель 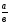 <
<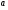 ,то
,то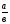 - дробь правильная
- дробь правильная 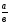
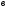
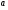 ,то
,то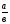 - дробь неправильная.
- дробь неправильная.
Правильная дробь меньше единицы, а неправильная дробь больше или равна единице
Путают числитель и знаменатель
4.Запись числа, содержащих целую и дробную части, называют смешанной (смешанное число)
смешанное число
дробь
Есть целая часть и дробная часть
конъюнктивная
через род и видовые отличия
обыкновенная дробь, натуральное число
Сложения целой части и дробной части
Перевод из смешанной дроби в неправильную.
Перевод из неправильной в смешанную дробь
При переводе из неправильной дроби путают куда писать неполное частное, остаток, делитель.
При переводе в смешанную дробь, что писать в знаменатель, как получается числитель.
Логико-математический анализ задач
В результате выполнения логико-математического анализа задач была проведена их классификация по уровню сложности и виду, на основании которой составлена таблица 2.
Таблица 2.
Классификация задач по теме «Обыкновенные дроби»
Типы задач /сложность
задачи
I уровень
сложности
II уровень
сложности
Задачи на вычисление
№883(а,б), 1011-1012,1017,1041.1043-1046.1059,1067,1084-1087.1094-1096.1115,1120
№883 (в, г),866,872
Текстовые задачи
№ 889-890, 898_908,985,989,996,1005-1010,1054-1057,1069-1079,1089-1091
№891,909,917-922,1019,1020,1043
Задачи на составление уравнений
№ 956-962
№ 867,869,870,
Практические
задачи
№850-853,885,886,892-893,940-944,1032,1088.1100
№855,1028,1029
Задачи
на сравнение
№ 946-948,1028, 1029
№862,952.1032,
Решение уравнений
№ 1018,
№ 1042.1058
Задания для поисковой, исследовательской работы
№865,866,1062,1098
№917, 1063.1132
Упражнения для работы в паре или группе
№854,856,868,918,921,923,924,955,962,964,1094.1096,1123,1126,1127
№871-873,
§ 3. Примеры решения типовых заданий и задач по теме, направленных на развитие и формирование УУД
Регулятивные УУД стоят в ряду важнейших умений, которые должны быть сформированы у каждого учащегося уже на начальном этапе изучения математики. Нужно давать детям возможность самостоятельно разбираться в новом материале, самостоятельно планировать ход изучения темы, выбирать уровень изучения и так же самостоятельно контролировать свои знания с последующей коррекцией. На уроках для этого надо применять систему заданий, направленных на поиск информации по заданному тексту, задачи с преднамеренными ошибками или направленные на поиск ошибки, самоконтроль и взаимоконтроль.
3.1. Фрагмент урока «открытия» новых знаний из главы
«Обыкновенные дроби» на тему
«Сложение дробей с одинаковыми знаменателями»
Цель: Изучение алгоритма сложения обыкновенных дробей. Развитие самостоятельного наблюдения, познавательного интереса, умения делать выводы, обобщения.
Этапы
Деятельность учителя
Деятельность учащихся
4. Выявление места и причины затруднения
На тарелке лежало 17 конфет. Вороненок Паша взял 2 конфеты. Какую часть конфет взял Паша?
Вороненок Гоша взял 3 конфеты. Какую часть взял Гоша?
Сколько всего конфет взяли воронята? Какую часть всех конфет они взяли всего? Что для этого нужно сделать?
А какую часть конфет составляют все конфеты?
Какая часть конфет осталась?
сложить дроби, вычесть
5. Целеполагание и построение проекта выхода из затруднения
- Что мы должны научиться делать?
- Значит перед нами стоят задачи:
- Хорошо! Чтобы продолжить работу, надо записать тему урока, что мы запишем в тетрадь?
складывать и вычитать дроби с одинаковыми знаменателями
научиться складывать и вычитать дроби с одинаковыми знаменателями и применять эти знания при решении задач.
Сложение и вычитание дробей с одинаковыми знаменателями
6. Реализация проекта.
-Ребята, сколько конфет всего? Как выполнить сложение дробей 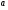 Вспомним что показывает числитель? Значит Паша взял 2 конфеты, а Гоша - 3. Всего сколько конфет взяли? (5). Выполним сложение. А сколько осталось? Как можно узнать? Выполним вычитание.
Вспомним что показывает числитель? Значит Паша взял 2 конфеты, а Гоша - 3. Всего сколько конфет взяли? (5). Выполним сложение. А сколько осталось? Как можно узнать? Выполним вычитание.
- А теперь давайте сформулируем правило сложения (вычитания) дробей с одинаковыми знаменателями. (говорят).
- Давайте откроем учебник на странице 118 и прочтём правила. Так ли мы их сформулировали? Замечательно! Эти правила надо знать!
(слайд, на котором буквенная запись сложения и вычитания)
- Ребята, запишите буквенную запись сложения и вычитания в тетрадь
Формулируют правила, проверяют текст правила.
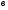
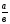
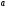
Так с помощью проблемного диалога учащиеся самостоятельно определяют свою границу знания -незнания, формулируют тему и цель урока, выдвигают задачи и собственные цели в изучении данного материала.
В итоге формируются следующие регулятивные УУД: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно, планирование: определение последовательности промежуточных действий с учётом конечного результата, составление плана действий.
3.2. Фрагмент урока отработки умений и рефлексии на тему «Сложение и вычитание смешанных дробей».
Цель: создать условия для осознания учащимися уровня и качества усвоения результата
Клоун придумал несколько примеров на сложение и вычитание смешанных дробей, а чтобы было смешно, стер в них некоторые числа, а где-то вычислил неправильно. Вот такие забавные равенства получились: Найдите ошибки или неправильный ответ (работа в парах).
-
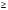 [10
[10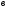 ]
] -
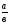 [
[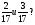 ]
] -
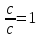 [7]
[7] -
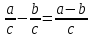 [
[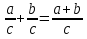 ]
] -
5
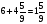 [
[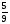 ]
] -
4 -
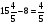 [
[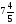 ]
]
Формируются следующие регулятивные УУД: выделение и осознание того, что уже пройдено, постановка цели учебной задачи, синтез, прогнозирование результата.
-
Все самостоятельные работы на этапе изучения новой темы можно проводить в форме взаимопроверки либо самоконтроля с обязательным нахождением ошибки, если они имеются.
3.3 Фрагмент самостоятельной работы на тему: «Сложение и вычитание смешанных дробей»
Цель: Проверить навыки сложения и вычитания смешанных дробей.
ПРОВЕРКА ЗНАНИЙ: самостоятельная работа (через копировку)
Iвариант:
а) Выполните действия:
1) 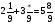 ; 2)
; 2) 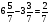 ; 3)
; 3) 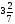 .
.
б) Решите уравнение: х+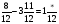 .
.
II вариант:
а) Выполните действия:
1) 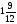 ; 2)
; 2)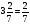 .
.
б) Решите уравнение: 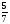 .
.
III вариант:
а) Выполните действия:
1) ![]() ; 2)
; 2) ![]() .
.
б) Решите уравнение: ![]() .
.
Регулятивные УУД: контроль в форме сравнения способа действия и его результата с заданным эталоном с целью обнаружения отклонений от эталона и внесение необходимых корректив, анализ собственной работы и полученных умений.
Средства обучения по теме:
Предписание при сложении (и вычитании) чисел в смешанной записи:
-
целые части дроби складываются (вычитаются) отдельно;
-
дробные части дроби складываются (вычитаются) отдельно;
Если при сложении смешанных чисел в их дробной части получается неправильная дробь, то из дробной части выделяют целую часть и добавляют ее к уже имеющейся целой части.
Пример: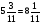
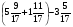 .
.
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, поступают так:
Пример: 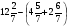
Короче: 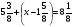 .
.
Если вычитают смешанную дробь или дробь их натурального числа, поступают так:
Пример:
1)  . 2)
. 2) 
Глава 2. Методические рекомендации обучения теме «Обыкновенные дроби»
1.Диагностические цели обучения теме «Обыкновенные дроби»
Таблица целей обучения теме «Обыкновенные дроби»
Формулировки целей-ориентиров
Учебные задачи (УЗ), направленные на формирование умений для достижения планируемых результатов:
Средства помощи
цель считается достигнутой, если Вы на уровнях:
базовом
повышенном
Ц I: целеполагание
В соответствии с картой темы ставит цели собственной деятельности и фиксирует их в индивидуальной таблице «Планирование УПД при изучении темы»
Ц II: приобретение учебной информации (УИ), формирование познавательных УУД при решении УЗ
а) анализирует текст учебника и составляет схему определения понятий;
б) анализирует решение задач из учебника, обобщает их решение помощью готового предписания в) подводит решение задачи под готовое предписание,
а) строит логической цепи рассуждения; выдвижение гипотез, их обоснование на сравнение, сверяясь с учебником; б) выполняет анализ и выявляет преобразования для выделения целой части числа и представлению смешанного числа в виде неправильной дроби; в) обобщает решение задач одного типа и составляет предписание, используя карточку-информатор.
а) даёте определение всех видов обыкновенных дробей; знаково-символические действия; б) выполняете анализ и выявляете действий, нужные для сложения и вычитания смешанных дробей, в) составляете приёмы их решений с помощью указаний
г) используете приобретенные знания и умения в межпредметных связях (информатика, экономика, технология);
д) используете справочную литературу для получения информации по данной теме
а) карточки-информаторы;
б) алгоритмы выполнения действий с обыкновенными дробями;
в) алгоритмы сравнения обыкновенных дробей;
г) макет: «Доли и дроби»;
д) таблица окружности и круга
Ц III:
Применение знаний при решении математических и учебных задач
Умеет:
-
изображать окружность данного радиуса с помощью циркуля; распознавать точки, принадлежащие окружности (кругу) и не принадлежащие им
-
читать и записывать обыкновенную дробь; находить значение дроби о числа и число по значению его дроби
-
сравнивать дроби с одинаковыми знаменателями; изображать их на числовом луче
-
распознавать правильные и неправильные дроби; отмечать их на координатном луче
-
складывать и вычитать дроби с одинаковыми знаменателями, смешанные числа
-
представлять частное в виде дроби и наоборот; записывать натуральное число в виде дроби с заданным знаменателем
-
представлять смешанное число в виде суммы целой и дробной частей; в виде неправильной дроби; выделять целую часть из неправильной дроби
1) приём саморегуляции;
3) таблицы с предписаниями;
4) карточки-информаторы
5)стандарты решений обыкновенных дробей
б) использовать основные алгоритмы и предписания для выполнения заданий 1-2-ого уровней сложности; в) использовать прием саморегуляции для выполнения заданий 1-2-ого уровней сложности
б) использовать все основные алгоритмы и предписания для выполнения заданий 3-го уровня сложности; в) использовать прием саморегуляции для выполнения заданий повышенного уровня сложности
Ц IV:
контроль знаний и умений, их коррекция.
Рефлексия
знает а) определения: 1) окружности, круг, радиус, диаметр круга и окружности, полуокружность, дуга окружности;
2) обыкновенные дроби, что показывает числитель, знаменатель, 3) правильные и неправильные дроби; 4) смешанные числа;
6) деление и дроби
б) формирует законы и правила: 1) выполнения арифметических действий, 2) сравнения дробей с одинаковым знаменателем, 3) нахождение неизвестных компонентов, 4) сложения и вычитания обыкновенных дробей с одинаковыми знаменателями; 5) распознавания правильные и неправильные дроби; отмечать их на координатном луче
в) проговаривает алгоритмы: 1) сравнение дробей; 2) сложение и вычитание дробей с одинаковыми знаменателями; 3) сложение и вычитание смешанных чисел; 4) выделения целой части числа и представлению смешанного числа в виде неправильной дроби;
г) приводите примеры в соответствии с определениями;
д) рассказывает краткие сведения из истории возникновения дробей;
е) делает выводы о дальнейших действиях, планирует коррекцию учебно-познавательной деятельности;
ж)выполняет рефлексию способов и условий действия, контроль действия.
знает виды обыкновенных дробей и их определения;
применяет свойства сложения и вычитания;
понимает мировоззренческое значение обыкновенных дробей
1) алгоритмы выполнения действий с обыкновенными дробями;
2) приём саморегуляции;
3) таблицы с предписаниями;
4) карточки-информаторы
Ц V: формирование КУД
а) работает в группе, оказывает взаимопомощь, рецензирует ответы товарищей; б) организует взаимоконтроль, взаимопроверку и др. на всех этапах учебно-познавательной деятельности (УПД) по выполненным заданиям предыдущих уровней с обоснованием; в) оказывает помощь, работающим на предыдущих уровнях; г) осуществляет поиск информации для подготовки письменного сообщения и устного выступления в соответствии с изучаемой темой, используя правила коммуникативного взаимодействия; д) выступает с сообщениями по истории математики, связи математики с искусством, практикой и др.;е) участвует в обсуждении выступлений
приёмы контроля, оценки;
Ц VI: формирование организационных умений
а) выбираете уровни достижения целей и формулируете цели своей учебной деятельности; б) выбираете задачи и решает их; в) осуществляете самопроверку с использованием образцов, приёмов; г) составляете контрольную работу для своего уровня усвоения; д) оцениваете свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; е) делает выводы по итогам предыдущей УПД, о дальнейших действиях, направленных на коррекцию, планирует коррекцию УПД.
приёмы саморегуляции УПД
1.2. Карта изучения темы и её использование
I. Последовательность уроков и цели изучения темы
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Ц
1,5
Ц
2-3
Ц 1-2
Ц 2-3
Ц 2-3
Ц
2 -5
Ц
1-4
Ц
3- 4
Ц
2-5
Ц
1-3
Ц 2-3
Ц
3-6
Ц
4,5,6
Ц 1, 2,3
Ц
2-4
Ц
2-4
Ц
1-3
Ц
2-4
Ц
1-3
Ц 2-4
Ц 1-3
Ц
2-4
Ц
2-4
Ц 3,4
Ц4,5,6
П. 22
П. 22
П. 23
П.
23
П. 23
П.
23
с/р
П.
24
П. 24
П.
24 с/р
П. 25
П. 25
К.Р.
Коррекция
П. 26,
25
П. 26,
25
П. 26 с/р
П.
27,
25, 26
П.
27,
25, 26
П.
28,
25,
26
П.28 25,
26
П.
29
26
П.
29,
26
с/р
П22,
29
Подг. к КР
К.Р.
Коррекция
II. Блок актуализации знаний учащихся
Знать:
-
(иметь) представление об окружности, обыкновенных дробях, смешанных числах
-
что показывает числитель и знаменатель
-
определение правильной и неправильной дробей
-
правила сложения и вычитания дробей с одинаковыми знаменателями
-
правила сложения и вычитания смешанных чисел
Уметь:
-
изображать окружность данного радиуса с помощью циркуля, обозначать и называть их элементы, распознавать точки, принадлежащие окружности
-
(кругу) и не принадлежащие им
-
читать и записывать обыкновенную дробь;
-
называть числитель и знаменатель дроби и объяснять, что ни показывают.
-
находить значение дроби от числа и число по значению его дроби
-
распознавать и решать три основные задачи на дроби.
-
сравнивать дроби с одинаковыми знаменателями; изображать их на числовом луче
-
распознавать правильные и неправильные дроби; отмечать их на координатном луче
-
записывать результат деления двух любых натуральных чисел с помощью обыкновенных дробей.
-
записывать любое натуральное число в виде обыкновенной дроби.
-
сравнивать правильные и неправильные дроби с единицей и друг с другом.
-
складывать и вычитать дроби с одинаковыми знаменателями, смешанные числа
-
представлять частное в виде дроби и наоборот; записывать натуральное число в виде дроби с заданным знаменателем
-
представлять смешанное число в виде суммы целой и дробной частей; в виде неправильной дроби; выделять целую часть из неправильной дроби
III. Предметные результаты (Ц 2, 3 таблицы целей): уметь решать вычислительные примеры на сложение и вычитание дробей с одинаковыми знаменателями, сравнивать дроби с одинаковыми знаменателями, распознавания правильные и неправильные дроби; отмечать их на координатном луче
и применять полученные знания для решения текстовых задач, используя понятия: определение правильной и неправильной дроби, смешанной дроби,
алгоритмы 1) сравнение дробей; 2) сложение и вычитание дробей с одинаковыми знаменателями; 3) сложение и вычитание смешанных чисел; 4) выделения целой части числа и представлению смешанного числа в виде неправильной дроби; применение формул: правил сложения и вычитания с одинаковыми знаменателями с помощью букв
YI. Образцы заданий итоговой контрольной работы (Ц 4,6)
Y. Средства обучения теме
1 уровень
Баллы
2 уровень
Баллы
3 уровень
Баллы
Контрольная работа №7
1)Вычислите:
а)  ;
;
б) 4 +  .
.
2) Сравните:
а) 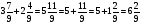 ; б)
; б) 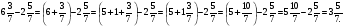
3) Решите уравнение:
2у-у+3∶7=1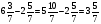 .
.
4) У ученика было 40 рублей. На покупку тетрадей он израсходовал 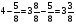 всех денег. Сколько рублей стоит тетрадь?
всех денег. Сколько рублей стоит тетрадь?
5) Начертите одну окружность с центром в точке С и радиусом 3 см, а затем с центром в той же точке С, но меньшего на 1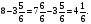 см радиуса?
см радиуса?
1
1
2
2
2
1). Длина прямоугольника 56 см. Ширина составляет ![]() длины. Найдите ширину прямоугольника.
длины. Найдите ширину прямоугольника.
2). На районной олимпиаде ![]() участников получили грамоты. Сколько участников было на олимпиаде, если грамоты получили 48 человек?
участников получили грамоты. Сколько участников было на олимпиаде, если грамоты получили 48 человек?
3). Сравните: а) ![]() и
и ![]() ; б)
; б) ![]() и
и ![]() .
.
4). Какую часть составляют:
а) 19 га от квадратного километра;
б) 39 часов от недели;
в) 37 г от 5 кг?
5). При каких натуральных значениях k дробь ![]() будет правильной?
будет правильной?
1
1
2
2
2
1) Примите за единичный отрезок длину 8 клеток тетради и отметьте на координатном луче точки А( ), М(
), М(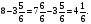 ), К(
), К( ), Д(
), Д( ), F(
), F( ) .
) .
2) Сравните числа:
а)  ; б)
; б)  ;
;
в) 1 и  ; г)
; г) 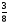 .
.
3) Сложите 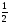 30 и
30 и 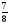 14.
14.
4) Какую часть составляет:
а) 9 см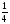 от квадратного дециметра;
от квадратного дециметра;
б) 17 дм 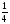 от кубического метра;
от кубического метра;
в) 13 кг от 2 ц?
5) Ширина прямоугольника 48 см, что составляет 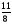 его периметра. Найдите длину этого прямоугольника.
его периметра. Найдите длину этого прямоугольника.
6) Составьте какую-либо дробь, знаменатель которой - наименьшее четырехзначное число, записанное различными цифрами и оканчивающееся на 8. Ответ поясните.
1
2
2
2
2
3
1) алгоритмы выполнения действий с обыкновенными дробями;
2) стандарты сравнений обыкновенных дробей
3) графическое изображение окружности
4) приём саморегуляции при
решении уравнений;
5)прием записи результата деления двух любых натуральных чисел с помощью обыкновенных дробей.
6) прием нахождения значения дроби от числа и число по значению его дроби.
1).Выполните действия:
а)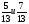 ;
;
б)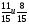 ;
;
в) 6 - 2 ;
;
г)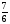 .
.
2)Турист шел с постоянной скоростью и за 3 ч прошел 14 км. С какой скоростью он шел?
3) В гараже 45 автомобилей. Из них
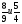 - легковые. Сколько легковых автомобилей в гараже?
- легковые. Сколько легковых автомобилей в гараже?
4) Решите уравнение:
а) 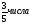 ;
;
б) 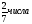 .
.
5) Какое число надо разделить на 8, чтобы частное равнялось  ?
?
1
1
1
1
2
1) Найдите значение выражения:
а)![]() б)
б) ![]() ;
;
в) ![]() .
.
2) За два дня было скошено ![]() луга. В первый день скошено
луга. В первый день скошено ![]() луга. Какую часть луга скосили во второй день?
луга. Какую часть луга скосили во второй день?
3) На изготовление одной детали требовалось по норме ![]() часа, но рабочий потратил на её изготовление на
часа, но рабочий потратил на её изготовление на ![]() часа меньше. На изготовление другой детали рабочий затратил на
часа меньше. На изготовление другой детали рабочий затратил на ![]() часа больше, чем на изготовление первой. Сколько времени затратил рабочий на изготовление этих двух деталей?
часа больше, чем на изготовление первой. Сколько времени затратил рабочий на изготовление этих двух деталей?
4) Решите уравнение:
а) ![]()
5) При делении числа р на 9 получилось ![]() . Найдите число р.
. Найдите число р.
1
1
2
1
3
1) Найдите значение выражения:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() .
.
2) За день удалось расчистить от снега ![]() аэродрома. До обеда расчистили
аэродрома. До обеда расчистили ![]() аэродрома. Какую часть аэродрома очистили от снега после обеда?
аэродрома. Какую часть аэродрома очистили от снега после обеда?
3) На приготовление домашних заданий ученица рассчитывала потратить ![]() часа, но потратила на
часа, но потратила на ![]() часа больше. На просмотр кинофильма по телевизору она потратила на
часа больше. На просмотр кинофильма по телевизору она потратила на ![]() часа меньше, чем на приготовление домашних заданий. Сколько всего времени потратила ученица на приготовление домашних заданий и на просмотр кинофильма?
часа меньше, чем на приготовление домашних заданий. Сколько всего времени потратила ученица на приготовление домашних заданий и на просмотр кинофильма?
4) Решите уравнение:
а) ![]() б)
б) ![]() .
.
5) При делении числа а на 12 получилось ![]() . Найдите число а.
. Найдите число а.
1
1
2
2
3
1) алгоритмы выполнения действий с обыкновенными дробями;
4) приём саморегуляции при
решении уравнений;
5)прием записи результата деления двух любых натуральных чисел с помощью обыкновенных дробей.
6) прием нахождения значения дроби от числа и число по значению его дроби.
Контрольная работа №8
YI. Задания для домашней работы (Ц 3,4,5, 6)
1 уровень (обязательный уровень стандарта): №№ 874, 925, 926, 965, 966, 967, 1000, 1001,1039, 1040, 1041, 1045, 1076, 1077, 1109, 1111,
2 уровень: №№ 875, 927,928, 929, 968, 969, 999, 1002, 1042, 1046, 1078, 1079,1110, 1136, 1137, 1138, 1727
3 уровень: №№ 876, 877, 931, 932, 933, 1043,1044, 1139, 1726
YII. Темы индивидуальных заданий (Ц 5,6)
1) Солнечные часы;
2) Монеты в старину на Руси;
3) Название дробей в старинных книгах;
4) История возникновения дробей, их обозначение.
5) Рассказ о числе
6) Математические факты связанные с кругом,
7) Старинные задачи на дроби
YIII. Метапредметные результаты: перечень учебных действий (умений) для освоения темы (Ц 1 - 5)
Познавательные УУД
Регулятивные УУД
Коммуникативные УУД
Личностные УУД
-
амостоятельное выделение и формулирование учебной цели;
-
знаково-символические действия;
-
выбор оснований и критериев для сравнения,
-
построение логической цепи рассуждения; выдвижение гипотез, их обоснование; обобщение, конкретизация, анализ;
-
составление схемы определения понятия, подведение под понятие;
-
постановка и решение проблемы при составлении задачи, осуществляют поиск и выделение необходимой информации
-
Выбор и принятие целей,
-
составление плана,
-
самоконтроль, самооценка,
-
соотнесение своих знаний с той учебной информацией, которую нужно усвоить;
-
приёмы саморегуляции,
-
оценивают достигнутый результат,
-
самостоятельно формируют познавательную цель и строят действия в соответствии с ней.
-
Взаимоконтроль, взаимопроверка, распределение обязанностей в группе,
-
умение слушать, выступать, рецензировать, писать текст выступлений, обмениваться знаниями между членами группы для принятия эффективных совместных решений,
-
разрешать конфликты на основе согласования позиций и учёта интересов;
-
формулировать, аргументировать и отстаивать своё мнение;
-
умение осознанно использовать речевые средства в соответствии с задачей коммуникации, для выражения своих чувств, мыслей и потребностей
-
Рефлексия собственной деятельности,
-
самопознание и самоопределение, смысло-образование.
-
способность ставить цели и строить жизненные планы
§ 5. Учебный план темы.
Тематическое и почасовое планирование образовательных результатов освоения математики
на 2014/2015 учебный год (фрагмент)
Класс 5 Б
Учитель Сазанова Т.В.
Количество часов : всего 170 часов; в неделю 5 часов.
Плановых контрольных уроков 14 ,
Административных контрольных уроков 3 ч.
Планирование составлено на основе
-
федерального компонента государственного стандарта общего образования,
-
примерной программы по математике основного общего образования,
-
федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2010-2011 учебный год,
-
с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования,
-
базисного учебного плана.
Учебник Математика 5, Н.Я. Виленкин, издательство «Мнемозина», 2014
Дополнительная литература
1. Чесноков А. С. , Нешков К.И. Дидактические материалы по математике для 5 класса-М.:Просвещение, 2014.
2. Попова Л.П.поурочные разработки по математике к УМК Н.Я.Виленкина и др. М.ВАКО,2014.380с.
№ урока
Дата проведения
Тема урока
Тип урока
Технологии
Решаемые проблемы
Виды деятельности (элементы содержания, контроль)
Планируемые результаты
Комментарий учителя
Предметные
УУД
Личностные
план
факт
1
2
2
3
4
5
6
7
8
9
10
11
Глава II. ДРОБНЫЕ ЧИСЛА (81 ч)
§ 5. Обыкновенные дроби (22 ч)
74
Окружность и круг
Урок
изучения
нового
Здоровьесбережения, проблемного обучения, развивающего обучения
Что общего и в чем различия у окружности и круга? Что называется радиусом, диаметром, дугой окружности?
Работа с текстом учебника, работа у доски и в тетрадях
Освоить понятия окружности и круга. Научиться применять циркуль для простейших геометрических построений. Вывести формулу зависимости между радиусом и диаметром одной окружности и применять полученные знания, умения и навыки при решении задач
Коммуникативные: воспринимать текст с учетом поставленной учебной задачи, находить в тексте информацию, необходимую для решения.
Регулятивные: формировать способность к мобилизации сил и энергии; способность к волевому усилию - выбору в ситуации мотивационного конфликта и к преодолению препятствий.
Познавательные: уметь выделять существенную информацию из текстов
Формирование навыков анализа, сопоставления, сравнения
75
19.12
Окружность и круг
Комбинированный урок
Здоровьесбережения, информационно-коммуникационные, поэтапного формирования умственных действий
Как решать задачи с окружностью и кругом?
Фронтальный опрос, работа у доски и в тетрадях
Научиться применять математическую терминологию и символьный язык при решении задач, связанных с окружностью и кругом
Коммуникативные: развивать умение обмениваться знаниями между одноклассниками для принятия эффективных совместных решений.
Регулятивные: проектировать траектории развития через включение в новые виды деятельности и формы сотрудничества. Познавательные: уметь осуществлять сравнение и классификацию по заданным критериям
Формирование мотивации к познавательной деятельности
76
22.12
Доли. Обыкновенные дроби
Урок
изучения
нового
Здоровьесбережения, личностно-ориентированного обучения, развивающего обучения, проектной деятельности
Как записывается дробью половина, треть, четверть? Что показывает знаменатель (числитель) дроби?
Математический диктант, работа у доски и в тетрадях
Научиться изображать дроби на координатном луче, называть числитель и знаменатель дроби. Называть доли метра, тонны, суток в соответствии с соотношением между единицами измерений
Коммуникативные: формировать коммуникативные действия, направленные на структурирование информации по данной теме. Регулятивные: формировать целевые установки учебной деятельности, выстраивать алгоритм действий.
Познавательные: уметь устанавливать причинно-следственные связи
Формирование навыков составления алгоритма выполнения задания, навыков выполнения творческого задания
77
23.12
Доли. Обыкновенные дроби
Урок
изучения
нового
Здоровьесбережения, развития исследовательских навыков, педагогики сотрудничества, личностно-ориентированного обучения
Как найти часть от числа, выраженную дробью?
Работа у доски и в тетрадях, индивидуальная работа (карточки-задания)
Освоить приемы решения задач на нахождение части от числа
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Регулятивные: определять последовательность промежуточных действий с учетом конечного результата, составлять план. Познавательные: уметь выделять существенную информацию из текстов
Формирование навыков анализа, творческой инициативности и активности
78
24.12
Доли. Обыкновенные дроби
Урок формирования и применения знаний, умений, навыков
Здоровьесбережения, проблемного обучения, развивающего обучения
Как найти число, если известна его часть, выраженная дробью? Как перевести более мелкие величины в более крупные?
Устный опрос. Работа у доски и в тетрадях
Освоить приемы решения задач на нахождение числа по его части; переводить именованные величины в соответственные более крупные единицы с использованием обыкновенных дробей
Коммуникативные: развивать умение обмениваться знаниями между одноклассниками для принятия эффективных совместных решений.
Регулятивные: проектировать траектории развития через включение в новые виды деятельности и формы сотрудничества. Познавательные: уметь осуществлять сравнение и классификацию по заданным критериям
Формирование навыков анализа
79
25.12
Доли. Обыкновенные дроби
Урок закрепления знаний
Здоровьесбережения, развития исследовательских навыков, развивающего обучения, самодиагностики и самокоррекции результатов
Как правильно решать задачи на части?
Работа у доски и в тетрадях, самостоятельная работа
Научиться классифицировать задачи на части по методу их решения
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Регулятивные: осознавать самого себя как движущую силу своего научения, к преодолению препятствий и самокоррекции. Познавательные: уметь осуществлять сравнение и классификацию по заданным критериям
Формирование устойчивой мотивации к индивидуальной деятельности по самостоятельно составленному плану
80
26.12
Сравнение дробей
Урок
изучения
нового
Здоровьесбережения, личностно-ориентированного обучения, развивающего обучения, проектной деятельности
Как сравнить дроби с помощью числового луча? Как сравнить дроби с равными знаменателями?
Работа с текстом учебника, работа у доски и в тетрадях
Научиться сравнивать дроби с помощью координатного луча, применять правило сравнения дробей с равными знаменателями и записывать результаты сравнения с использованием математической символики
Коммуникативные: уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.
Регулятивные: определять последовательность промежуточных целей с учетом конечного результата; составлять план последовательности действий.
Познавательные: использовать поиск и выделение необходимой информации, анализ с целью выделения общих признаков, синтез, как составление целого из частей
Формирование навыков составления алгоритма выполнения задания
81
12.01
Сравнение дробей
Урок закрепления знаний, умений, навыков
Здоровьесбережения, личностно-ориентированного обучения, развивающего обучения, проектной деятельности
Можно ли сравнить? Как сравнить дроби с равными числителями?
Фронтальная работа с классом, работа у доски и в тетрадях
Научиться упорядочивать дроби с равными знаменателями и применять полученные знания и умения при решении задач. Иметь представление о сравнении дробей с равными числителями
Коммуникативные: формировать коммуникативные действия, направленные на структурирование информации поданной теме. Регулятивные: формировать постановку учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно.
Познавательные: уметь устанавливать причинно-следственные связи
Формирование устойчивой мотивации к обучению на основе алгоритма выполнения задачи
82
13.01
Правильные и неправильные дроби
Урок
изучения
нового
Здоровьесбережения, личностно-ориентированного обучения, парной и групповой деятельности
Что называется правильной(неправильной) дробью? Можно ли сравнить правильную и неправильную дроби?
Работа в группах, фронтальная работа с классом
Дать определение правильной и неправильной дроби, научиться сравнивать правильную дробь с неправильной и применять полученные знания для оценки результата
Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений.
Регулятивные: составлять план последовательности действий; формировать способность к волевому усилию в преодолении препятствий.
Познавательные: уметь осуществлять сравнение и классификацию по заданным критериям
Формирование познавательного интереса к изучению нового
83
14.01
Правильные и неправильные дроби
Урок обобщения и систематизации
Здоровьесбережения, развития исследовательских навыков, информационно-коммуникационные, дифференцированного подхода в обучении
Что мы узнали о долях и дробях?
Работа у доски и в тетрадях, индивидуальная работа (карточки-задания)
Систематизировать знания по теме «Доли и дроби»
Коммуникативные: формировать коммуникативные действия, направленные на структурирование информации поданной теме. Регулятивные: осознавать учащимся уровень и качество усвоения результата. Познавательные: произвольно и осознанно владеть общим приемом решения задач
Формирование навыков самоанализа и самоконтроля
84
15.01
Контрольная работа № 7 по теме «Обыкновенные дроби»
Урок проверки, оценки и коррекции знаний
Здоровьесбережения, развития исследовательских навыков, развивающего обучения, самодиагностики и самокоррекции результатов
Проверка знаний учащихся по теме «Обыкновенные дроби»
Написание контрольной работы
Научиться применять знания, умения при решении задач на дроби
Коммуникативные: управлять своим поведением (контроль, самокоррекция, оценка своего действия).
Регулятивные: осознавать учащимся уровень и качество усвоения результата. Познавательные: ориентироваться на разнообразие способов решения задач
Формирование навыков самоанализа и самоконтроля
85
16.01
Сложение и вычитание дробей с одинаковыми знаменателями
Урок
изучения
нового
Здоровьесбережения, личностно-ориентированного обучения, педагогики сотрудничества
Как сложить (вычесть) две дроби с одинаковыми знаменателями?
Анализ ошибок, допущенных в контрольно работе, фронтальная работа с классом
Выучить правило сложения (вычитания)дробей с равными знаменателями и применять его при решении примеров, уравнений и задач
Коммуникативные: учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его. Регулятивные: осознавать самого себя как движущую силу своего научения, к преодолению препятствий и самокоррекции; уметь выполнять работу над ошибками. Познавательные: выбирать наиболее эффективные способы решения задач
Формирование устойчивой мотивации к обучению на основе алгоритма выполнения задачи
86
19.01
Сложение и вычитание дробей с одинаковыми знаменателями
Урок формирования и применения знаний, умений, навыков
Здоровьесбережения, проблемного обучения, развивающего обучения
Как записать в виде формулы правило сложения двух дробей с одинаковыми знаменателями?
Устный опрос, работа у доски и в тетрадях
Научиться записывать правило сложения(вычитания) дробей в буквенной форме. Применять полученные знания и умения для решения задач
Коммуникативные: слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения. Регулятивные: формировать постановку учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно.
Познавательные: выбирать наиболее эффективные способы решения задач
Формирование познавательного интереса
87
20.01
Деление и дроби
Урок
изучения
нового
Здоровьесбережения, личностно-ориентированного обучения, развивающего обучения, проектной деятельности
Как связаны дробная черта и знак деления?
Фронтальная работа с классом, работа у доски и в тетрадях
Научиться записывать деление в виде дроби и наоборот и использовать полученные навыки при решении задач
Коммуникативные: формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы. Регулятивные: проектировать траектории развития через включение в новые виды деятельности и формы сотрудничества. Познавательные: уметь осуществлять сравнение и классификацию по заданным критериям
Формирование устойчивой мотивации к обучению
88
21.01
Деление и дроби
Комбинированный урок
Здоровьесбережения, развития исследовательских навыков, педагогики сотрудничества, личностно-ориентированного обучения
Как разделить сумму на натуральное число? Как обосновать это свойство с помощью правила сложения дробей?
Работа у доски и в тетрадях, индивидуальная; работа(карточки-задания)
Понимать свойство деления суммы на число и применять его для упрощения вычислений
Коммуникативные: уметь выслушивать мнение членов команды, не перебивая; принимать коллективные решения. Регулятивные: формировать постановку учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно.
Познавательные: выбирать наиболее эффективные способы решения задач
Формирование устойчивого интереса к творческой деятельности, проявления креативных способностей
89
22.01
Смешанные числа
Комбинированный урок
Здоровьесбережения, проблемного обучения, развития исследовательских навыков, дифференцированного подхода в обучении
Что называется смешанным числом? Как выделить целую часть из неправильной дроби?
Самостоятельная работа, работа с текстом учебника, работа у доски и в тетрадях
Расширить представление о числе, научиться называть целую и дробную части смешанного числа, выделять целую часть из неправильной дроби
Коммуникативные: уметь находить в тексте информацию, необходимую для решения задачи.
Регулятивные: формировать способность к мобилизации сил и энергии; способность к волевому усилию - выбору в ситуации мотивационного конфликта и к преодолению препятствий.
Познавательные: уметь осуществлять анализ объектов с выделением существенных и несущественных признаков
Формирование навыков анализа
90
23.01
Смешанные числа
Урок овладения новыми знаниями, умениями, навыками
Здоровьесбережения, проблемного обучения, развивающего обучения
Как представить смешанное число в виде неправильной дроби?
Работа у доски и в тетрадях, индивидуальная работа (карточки-задания)
Научиться представлять смешанное число в виде неправильной дроби и применять эти знания и умения для решения задач
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Регулятивные: осознавать самого себя как движущую силу своего научения, к преодолению препятствий.
Познавательные: произвольно и осознанно владеть общим приемом решения задач
Формирование устойчивой мотивации к изучению и закреплению нового
91
26.01
Сложение и вычитание смешанных чисел
Урок
изучения
нового
Здоровьесбережения, развития исследовательских навыков, развивающего обучения, самодиагностики и самокоррекции результатов
Как сложить (вычесть) два смешанных числа?
Математический диктант, работа у доски и в тетрадях
Освоить алгоритм сложения (вычитания) смешанных чисел
Коммуникативные: развивать умение точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии. Регулятивные: вносить необходимые дополнения и коррективы в план и способ действия в случае расхождения эталона, реального действия и его продукта.
Познавательные: уметь осуществлять сравнение и классификацию по заданным критериям
Формирование устойчивой мотивации к обучению на основе алгоритма выполнения задачи
92
27.01
Сложение и вычитание смешанных чисел
Комбинированный урок
Здоровьесбережения, педагогики сотрудничества, развивающего обучения
Как применить смешанные числа при решении задач?
Работа у доски и в тетрадях, самостоятельная работа
Научиться применять сложение и вычитание смешанных чисел для решения уравнений и задач
Коммуникативные: формировать коммуникативные действия, направленные на структурирование информации поданной теме. Регулятивные: обнаруживать и формулировать учебную проблему, составлять план выполнения работы.
Познавательные: выбирать наиболее эффективные способы решения задач
Формирование познавательного интереса к изучению нового
93
28.01
Сложение и вычитание смешанных чисел
Урок обобщения и систематизации знаний
Здоровьесбережения, информационно-коммуникационные, поэтапного формирования умственных действий
Как применять сложение и вычитание дробей при решении задач, уравнений, примеров?
Фронтальная работ с классом, индивидуальная работа (карточки-задания)
Систематизировать приобретенные знания, умения, навыки по теме «Сложение и вычитание обыкновенных дробей»
Коммуникативные: развивать умение обмениваться знаниями между одноклассниками для принятия эффективных совместных решений.
Регулятивные: корректировать деятельность: вносить изменения в процесс с учетом возникших трудностей и ошибок, намечать способы их устранения.
Познавательные: ориентироваться на разнообразие способов решения задач
Формирование навыков самоанализа и самоконтроля
94
29.01
Контрольная работа № 8 по теме «Сложение и вычитание смешанных чисел»
Урок проверки, оценки и коррекции знаний
Здоровьесбережения, развития исследовательских навыков, развивающего обучения, самодиагностики и самокоррекции результатов
Проверка знаний учащихся по теме «Сложение и вычитание смешанных чисел»
Написание контрольной работы
Научиться воспроизводить приобретенные знания, умения, навыки в конкретной деятельности
Коммуникативные: управлять своим поведением (контроль, самокоррекция, оценка своего действия).
Регулятивные: формировать способность к мобилизации сил и энергии; способность к волевому усилию в преодолении препятствий.
Познавательные: произвольно и осознанно владеть общим приемом решения задач
Формирование навыков самоанализа и самоконтроля
95
30.01
Резерв. Решение
задач
Урок-практикум
Здоровьесбережения, личностно-ориентированного обучения, развивающего обучения, проектной деятельности
Применение обыкновенных дробей в практической деятельности
Анализ ошибок, допущенных в контрольной работе, фронтальная работа по решению задач
Научиться применять приобретенные знания, умения, навыки для решения практических задач
Коммуникативные: учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его. Регулятивные: осознавать учащимся уровень и качество усвоения результата. Познавательные: выбирать наиболее эффективные способы решения задач
Формирование познавательного интереса
§ 6. Примеры реализации целей обучения теме.
3. Фрагменты уроков с использованием ЦОР и здоровьесберегающих технологий в соответствии с темой «Обыкновенные дроби».
3.1.Фрагмент урока математики в 5 классе по теме «Обыкновенные дроби»
Оборудование урока: интерактивная доска, тест, карточки с заданиями, листочки настроения.
Ход урока
Мотивация учебной деятельности.
Учитель. Ребята, для того, чтобы узнать, что мы будем сегодня изучать на уроке, нам нужно ответить на вопрос: Без чего не могут обойтись охотники, барабанщики и математики? А для этого отгадаем кроссворд:
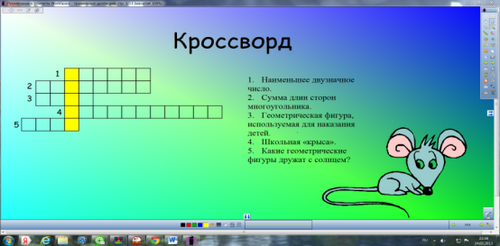
Правильный ответ записан в выделенном столбце.
Актуализация опорных знаний.
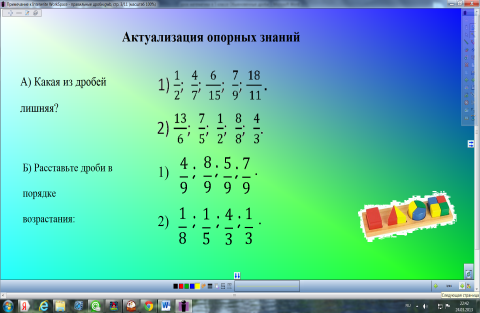
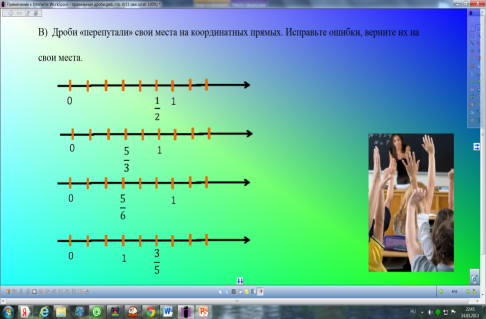
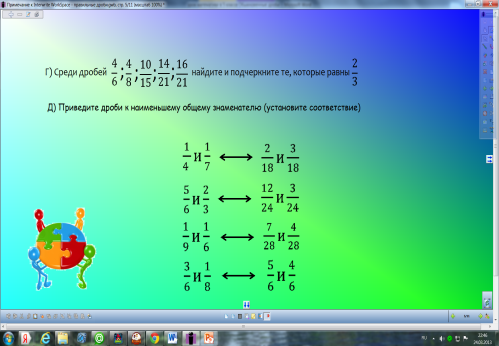
3. Тест.
Учащиеся выполняют тест на карточках, а в тетрадях записывают свои ответы. После того, как листочки сдали, проверяют ответы с доской.
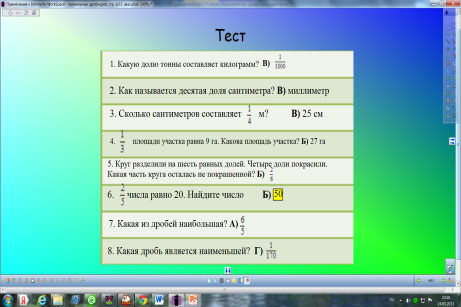
Физминутка.
Ну-ка в сторону карандаши,
Ни тетрадей, ни ручек, ни мела.
Вы устали, ребята, сейчас отдохнём,
Чтобы дальше работать нам смело.
Дружно встали, делаем зарядку:
(если согласны с утверждением - руки вверх, если нет - вперёд).
Из истории математики (презентация)
Работа в группах.
Класс делится на группы. Каждая команда получает карточки-задания, выполняют их. По полученным ответам находят в таблицах соответствующие буквы и составляют слово.
математика учебный дробь логический
6.2. План-конспект урока математики «Сравнение дробей с одинаковыми знаменателями»
Цель урока: Формирование способности учащихся к новому способу действия, расширение понятийной базы, формирование умения различать равные и неравные дроби, применять полученные знания при выполнении сравнения дробей.
Задачи урока:
- обучающие: (формирование познавательных и логических УУД)
- ввести понятие равных дробей с разными числителями;
- научить сравнивать обыкновенные дроби;
- сформировать умение применять алгоритм сравнения обыкновенных дробей при решении примеров.
-развивающие: (формирование регулятивных УУД)
- развивать умение анализировать, сравнивать и делать выводы;
- развивать устную речь;
-воспитательные: (формирование коммуникативных и личностных УУД)
- воспитывать умение высказывать свое мнение;
- воспитание умения участвовать в диалоге;
- формировать способность к позитивному сотрудничеству.
Планируемый результат (УУД):
Этап урока
Деятельность учителя
Деятельность учащегося
Познавательная
Коммуникативная
Регулятивная
Осуществляемые действия
Осуществляемые действия
Формируемые способы деятельности
Осуществляемые действия
Формируемые способы деятельности
Осуществляемые действия
Формируемые способы деятельности
Организационный
Приветствую учащихся, сообщаю тему и структуру урока
Настраиваются на работу
Ставят перед собой цель: «Что я хочу узнать сегодня на уроке»
Концентрируют внимание
Планируют учебное сотрудничество с учителем и одноклассниками
Получают позитивный заряд
самоопределяются и настраиваются на урок
Актуализация знаний
Организую индивидуальное повторение определения правильной и неправильной дроби;
Устное решение заданий типа: «Какую часть года составляет месяц?»;
«Какую часть тонны составляет килограмм?» и т.д.
Повторяют определение правильной и неправильной дроби
Анализируя и сравнивая предлагаемые задания, извлекают необходимую информацию для построения математического высказывания
Выполняют задания
Выражают свои мысли с достаточной полнотой и точностью, используют чужие высказывания для обоснования своего суждения
Закрепляют умение записывать число в виде дроби
Выполняют тренировочное учебное действие
Создание проблемной ситуации
Организую обсуждение «Можно ли сравнить ….? Что для Вас значит сравнить?»
Подвожу к понятию сравнения дробей
Построение логической цепи рассуждений и выдвижение гипотез и их обоснование
Анализируя и сравнивая выбираемые задания, извлекают необходимую информацию для введения нового понятия. Составляют план достижения цели и определяют средства
Отвечают на задаваемые вопросы в процессе обсуждения, сотрудничают в поиске и выборе информации
Выражают свои мысли с достаточной полнотой и точностью, аргументируют свое мнение
Участвуют в диалоге и выводят правило сравнения обыкновенных дробей
При возникновении ситуации затруднения регулируют ход мысли
Формирование проблемы: тема и цель урока
Вывожу на формулировку темы и целей урока. Четко проговариваю тему и цель урока
Приводят примеры сравнения дробей
Анализируя и сравнивая приводимые примеры, извлекают необходимую информацию для подведения под новое понятие, формулируют понятие правильно и неправильной дроби
Выходят на необходимость формулирования правила сравнения дробей
Выражают свои мысли с достаточной полнотой и точностью, аргументируют свое мнение
Участвуют в диалоге и учатся приводить примеры
В ситуации затруднения регулируют ход мыслей
Открытие нового знания
Организую работу с учебником, путем подводящего диалога побуждаю учащих к формулированию правила сравнения обыкновенных дробей
Учатся применять определения в процессе открытия нового знания
Выделяют необходимую информацию, планируют свою деятельность, прогнозируют результат
Работают в парах с учениками и учатся сотрудничать с учителем во время фронтальной работы класса
Планируют сотрудничество с одноклассниками и учителем
Вступают в диалог во время парной работы
В ситуации затруднения регулируют свою деятельность
Первичное применение нового знания
Организую работу по выполнению № 941, 942, 943, 944, 945, с последующей проверкой ответов и алгоритмов рассуждения в процессе решения
Учатся применять определения в процессе самостоятельной решения или работы у доски или в парной работы
Самостоятельно планирует свою деятельность, применяет способы решения и прогнозирует результат. Выстраивает в процессе решения задач логическую цепь рассуждений
Управление поведением партнера, контроль и коррекция, оценка действий партнера
Планируют сотрудничество с одноклассниками и учителем, учитывают мнение в паре и координируют свои действия
Контроль за работой своей и партнера, оценка и коррекция деятельности
Проявляют познавательную инициативу
Самостоятельная работа по закреплению изученного ранее
Организую работу по выполнению № 946 и 947 с последующей проверкой
Учатся применять полученные знания в процессе индивидуальной работы
Самостоятельно выполняют действия по алгоритму
Выполняют задание на сравнение обыкновенных дробей
Осознают применяемый алгоритм с достаточной полнотой
Контроль за правильностью выполнения заданий, осознание качества и уровня усвоения
Проявляет познавательную инициативу. Контролируют свои действия
Рефлексия
Организую обсуждение: Какова была тема урока? Какую задачу ставили? Каким способом решали поставленную задачу? И т.д.
Проводят рефлексию способов и условий своих действий
Планируют сотрудничество, используют критерии для обоснования своих суждений
Проводят самооценку
Домашнее
задание
Обсуждение домашнего задания № 951, 965, 966
Средства обучения по теме:
Предписание для сравнения дробей с одинаковыми знаменателями
![]()
Если a > b
 >
> 
да
нет
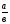 <
< 
Сравнение дробей с одинаковыми знаменателями
6.3. План-конспект урока математики «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями» с применением ЭОР
Цель урока: формирование навыков сложения и вычитания дробей с одинаковыми знаменателями.
Задачи:
- обучающие: (формирование познавательных и логических УУД) научить складывать и вычитать дроби с одинаковыми знаменателями
-развивающие: (формирование регулятивных УУД) развивать умение ставить перед собой цель - целеполагание, как постановку учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно; и планировать свою работу - планирование - определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий; контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона.
-воспитательные: (формирование коммуникативных и личностных УУД) учиться планированию учебного сотрудничества с учителем и сверстниками; учиться умению осознанно и произвольно строить речевое высказывание в устной и письменной форме; учиться смыслообразованию т. е. установлению учащимися связи между целью учебной деятельности и ее мотивом, другими словами, между результатом-продуктом учения, побуждающим деятельность, и тем, ради чего она осуществляется.
Средства обучения по теме:
Предписание при сложении (и вычитании) чисел в смешанной записи:
-
целые части дроби складываются (вычитаются) отдельно;
-
дробные части дроби складываются (вычитаются) отдельно;
Если при сложении смешанных чисел в их дробной части получается неправильная дробь, то из дробной части выделяют целую часть и добавляют ее к уже имеющейся целой части.
Пример: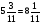
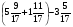 .
.
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, поступают так:
Пример: 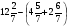
Короче: 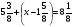 .
.
Если вычитают смешанную дробь или дробь их натурального числа, поступают так:
Пример:
1)  . 2)
. 2) 
План - конспект урока по теме
«Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями»
№
Этап урока
Деятельность учителя
Деятельность ученика
Название
используемых ЭОР
Время
Формируемые УУД
Познавательные
Регулятивные
Коммуникативные
Личностные
1.1
Орг. момент
Определяет
готовность учащихся. Сосредоточивает внимание учащихся
Готовят тетради и д/з для проверки
1 мин.
Организация своей учебной деятельности
Умение слушать, планирование учебного сотрудничества
1.2
Мотивация к учебной деятельности
Координирует деятельность учащихся
Устно решают задачи, повторяют теорию
2 мин
Анализ, сравнение, аналогия, использование знаковой системы, осознанное построение речевого высказывания, подведение под понятие
Целеполагание,
выполнение пробного учебного действия, фиксация индивидуального затруднения, волевая саморегуляция в ситуации затруднения
Выражение своих мыслей, аргументация своего мнения, учёт разных мнений учащихся,планирование учебного сотрудничества
Смыслообразование
1.3
Актуализация знаний, постановка проблемы и ее решение
Мотивирует учащихся.
Проводит диагностику универсальных учебных действий учащихся, сформированных в начальной школе по данной теме; развивает логическое и критическое мышление
Называют и записывают
тему урока.
Выполняют задания предложенные учителем. Оценивают результаты
15 мин.
Умение осознанно и произвольно строить речевое высказывание в устной форме; построение логической цепи рассуждений;
подведение под понятие; установление причинно-след-ственных связей
анализ, сравнение, аналогия, использование знаковой системы, осознанное построение речевого высказывания, подведение под понятие
Планирование,
выполнение пробного учебного действия, волевая саморегуляция в ситуации затруднения
Выражение своих мыслей, аргументация своего мнения, учёт разных мнений учащихся
2.1
Объяснение нового материала
Вводит определение сложения и вычитания обыкновенных дробей с одинаковыми знаменателями
Демонстрирует ЭОР;
организует деятельность работы с учебником; направляет работу учащихся
Слушают, отвечают на вопросы, делают выводы, работают с учебником;
Ведут записи в тетрадях
Сложение обыкновенных дробей с одинаковыми знаменателями.
Информационный модуль
Вычитание обыкновенных дробей с одинаковыми знаменателями
Информационный модуль
10 мин
Поиск и выделение необходимой информации;
знаково-символические действия,
умение осознанно и произвольно строить речевое высказывание в устной и письменной форме;
определение основной и второстепенной информации;анализ, сравнение, обобщение, подведение под понятие, постановка и формулирование проблемы, построение речевого высказывания
Анализ;
синтез,
установление причинно-следственных связей, волевая саморегуляция в ситуации затруднения
Выражение своих мыслей, аргументация своего мнения, учёт разных мнений, разрешение конфликтной ситуации
Самоопределение, смыслообразование
2.2
Первичное закрепление
Физминутка
( гимнастика для глаз под музыкальное сопровожде
ние
Следим глазами за движущимися объектами.
Мотивирует учащихся.
Ставит проблемные вопросы;
учит складывать и вычитать обыкновенные дроби
Решают поставленные задачи, отвечают на вопросы.
Игровое задание. Сложение обыкновенных дробей с одинаковыми знаменателями.
Практический модуль (игра)
Игровое задание
Вычитание обыкновенных дробей с одинаковыми знаменателями
Практический модуль (игра)
Видеофрагмент из балета Чайковского «танец феи драже »
12 мин
Поиск и выделение необходимой информации;
знаково-символические действия,
умение осознанно и произвольно строить речевое высказывание в устной и письменной форме; выбор оснований и критериев для сравнения.
Планирование - определение последовательности промежуточных целей с учетом конечного результата;,
анализ;
синтез,
установление причинно-следственных связей,
Планирование учебного сотрудничества с учителем и сверстниками;
умение слушать и вступать в диалог;
участвовать в коллективном обсуждении;
принятие решения
Самоопределение, смыслообразование
2 урок
2.3
Математический диктант
Организует и контролирует деятельность учащихся
Письменно решают представленные задачи,
отвечают на вопросы
Математический диктант. Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
Контролирующий модуль
8 мин
Анализ, синтез, аналогия, классификация, подведение под понятие, выполнение действий по алгоритму
Контроль, коррекция, оценка
Умение слушать и вступать в диалог, оценка действий
Смыслообразование
3.1
Самотоятельная работа с взаимопроверкой
Организует самостоятельную деятельность учащихся, взаимопроверку.
Воспитывает способность принимать самостоятельные решения; развивает навыки самоконтроля
Самостоятельно выполняют задания теста, затем проверяют в парах по ключу
10 мин
Установление причинно-следственных связей;
построение логической цепи рассуждений; контроль и оценка процесса и результатов деятельности;
рефлексия способов и условий действия, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
Контролируют процесс и результат учебной математической деятельности;
контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
коррекция; способность к волевому решению
Планирование учебного сотрудничества с учителем и сверстниками ;
Смыслообразование
3.2
Работа в парах
Физкультминутка
Выявляет границы применения нового задания, организует выполнение тренирующих заданий
Выполняют задания, закрепляют правила
Видеофрагмент из балета Чайковского «танец цветов »
9 мин
Использование знаково -символических средств, Моделирование и преобразование моделей; установление причинно-следственных связей; выполнение действий по алгоритму;
Извлечение необходимой информации из прослушанных текстов различных жанров;
Анализ контроль;
коррекция; оценка.
Инициативное сотрудничество в поиске и сборе информации, контроль, коррекция, оценка действий партнёра умение с достаточной полнотой и точностью выражать свои мысли
Нравственно-эстетическое оценивание усваиваемого материала
3.3
Работа в группах
организует выполнение тренирующих заданий, способствующих закреплению материала
Выполняют задания в группах
Задача в картинках на сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
Контролирующий модуль
10 мин
Построение логической цепи рассуждений, анализ, обобщение, подведение под понятие
Контроль, коррекция, самооценка
Выражение своих мыслей, достижение договорённости и согласование общего решения.
Осознание ответственности за общее дело
4.1
Рефлексия деятельности на уроке. Подведение итогов урока.
Постановка домашнего задания.
Мотивирует учащихся на подведение итогов урока Выявляет уровень усвоения изученного материала. Комментирует домашнее задание
Обобщают изученный материал.
Делают вывод.
Оценивают свою работу. Записывают домашнее задание.
3 мин
Ррефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, адекватное понимание причин успеха или неуспеха
Оценка - выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения
Самооценка на основе критерия успешности;
аргументация своего мнения, планирование учебного сотрудничества
Самоопределение
ЗАКЛЮЧЕНИЕ
Математика - важнейшая наука, созданная нашей цивилизацией и сопро-
вождающая ее на всех этапах развития. Вся современная наука: физика и хи-
мия, биология и экономика, лингвистика и социология не только использует
математические методы, но и строится по математическим законам. Путь в современную науку и технику, просто в современную жизнь лежит через математику. Этот элемент научного знания является важнейшей частью математического образования.
Термин универсальные учебные действия означает способность субъек-
та к саморазвитию через сознательное и активное присвоение социального
опыта, совокупность способов действия учащегося, а также связанных с ними навыков учебной работы, обеспечивающих его способность к самостоятельному усвоению новых знаний и умений. Таким образом, актуальной становится проблема создания механизмов формирования УУД: для чего необходимо выявлять теоретические основы обучения каждой теме, связанные с реализацией ФГОС ООО; выполнять отбор средств обучения теме, в том числе средства ИКТ; разрабатывать таблицы целей и карты обучения теме.
Решение поставленных задач потребовало использования следующих методов исследования: анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; тестирование учащихся, проведение опытной проверки.
Образование должно развиваться, так как развивается мир, страна, каждый из нас, и тогда школа сможет выполнить заказ государства
по воспитанию и развитию подрастающего поколения.
Тематика исторических сведений.
1.Из истории возникновения обыкновенных дробей.
2.Старинные задачи на дроби и их решение
3.Математика в стихах «Обыкновенные дроби»
4.Дроби в музыке важны - с математикой дружны!
5.Математический строй музыки
6.Зачем людям нужны дроби?
Список литературы
-
Федеральный государственный образовательный стандарт общего основного образования / М-во образования и науки Рос. Федерации. - М.: Просвещение, 2011. - 48 с
-
Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под ред. А.Г. Асмолова. - М.: Просвещение, 2010. - 159 с.
-
Данилюк А.Я., Кондаков А.М., Тишков В.А.. Концепция духовно-нравственного развития и воспитания личности гражданина России. - М.: Просвещение, 2009. - 24 с.
-
Примерные программы по математике. - М.: Просвещение, 2010. - 67 с.
-
Боженкова Л.И. Формирование УУД в обучении математике: типовые задания. Москва, 2015-139с..
-
Попова Л.П., Поурочные разработки по математике.-М: Вако,2014.-180с..
Интернет-ресурсы
-
- ФГОС общего образования и разработанные к ним документы.
-
- каталог Единой коллекции цифровых образовательных ресурсов.
-
- каталог электронных образовательных ресурсов ФЦ.
-
- электронные образовательные ресурсы.
-
- электронные образовательные ресурсы.
-
- «Сеть творческих учителей».
-
- портал "Информационно-коммуникационные технологии в образовании".
-
- видеолекции авторов УМК по школьной математике.
-
- газета «Математика» Издательского дома «Первое сентября».
-
Центральный образовательный портал. Содержит нормативные документы Министерства образования и науки, стандарты, информацию о проведении экспериментов.
-
Федеральный центр информационно-образовательных ресурсов
-
Портал «Учеба».
-
Банк педагогического опыта.
-
Популярные лекции по математике.
-
Дидактические материалы по информатике и математике.
-
МЦНМО. Математические праздники, олимпиады, базы данных задач с решениями, математическое образование в документах, статьях, публикациях, математические игры и др.